Fórmulas de estadística unidimensional
Frecuencias y porcentajes
| Frecuencias | Absoluta (fi) | Relativa (hi) | Acumulada (Fi) |
|---|---|---|---|
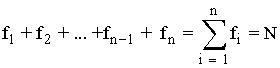 |
| Porcentaje | pi | acumulado (Pi) |
|---|---|---|
Medidas de centralización
Media aritmética
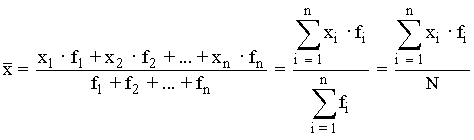
Media ponderada
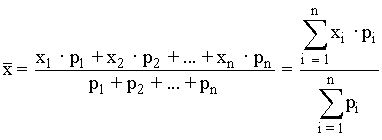
Tablas de frecuencia para variables estadísticas continuas
Marca de clase y amplitud del intervalo
![]()
![]()
Para un número de
datos grande:
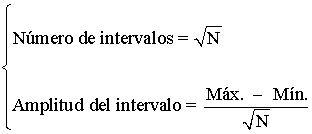
Moda
Variable estadística con mayor frecuencia absoluta. Para variables continuas hay que utilizar la ecuación:
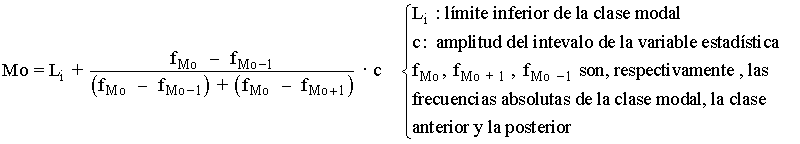
Mediana
Primera variable estadística cuya frecuencia absoluta acumulada exceda de la mitad del número de datos.
Para variables continuas hay que utilizar la ecuación:
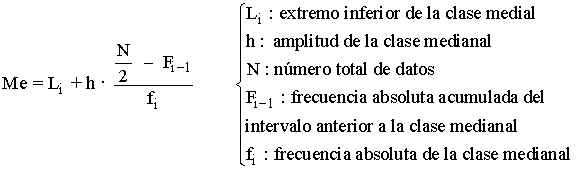
Medidas de posición: cuartiles, deciles y percentiles
Cuartiles
Tres valores de la variable estadística que divide en cuatro partes el número de datos.
Para variables continuas hay que utilizar la ecuación:
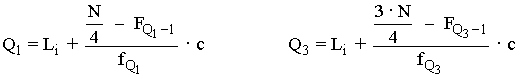
Rango intercuartílico : r = Q3 - Q1
La mediana coincide con el cuartil dos (Me = Q2)
Deciles
Nueve valores de la variable estadística que dividen en diez partes el número de datos.
Para variables continuas hay que utilizar la ecuación:
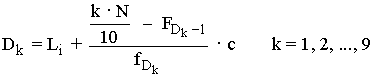
Percentiles
99 valores de la variable estadística que dividen en 100 partes el número de datos.
Para variables continuas hay que utilizar la ecuación:
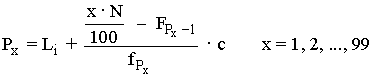
Medidas de dispersión
| Medida | Cálculo | Definición |
|---|---|---|
| Rango o recorrido | Es la diferencia entre el valor máximo y el valor mínimo de la variable. | |
| Recorrido relativo | 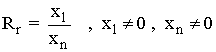 |
Es el cociente entre el valor mínimo y el valor máximo de la variable. |
| Desviación | Es la diferencia entre un valor cualquiera y la media. | |
| Varianza | 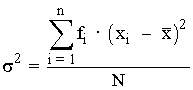 |
Es la media de los cuadrados de las desviaciones. |
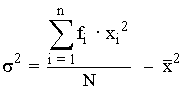 |
||
| Desviación típica | 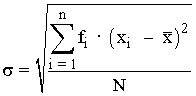 |
Es la raíz cuadrada positiva de la varianza. |
| Coeficiente de variación de Pearson | Es el cociente de la desviación típica y la media. |
Puntuaciones típicas o normalizadas
Para comparar datos correspondientes a dos distribuciones distintas, debemos tipificar (o normalizar) los valores.
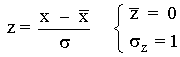


 INICIO
INICIO
