Estudio conjunto de la media y la varianza

En la mayoría de las ocasiones un conjunto de datos tienen un comportamiento normal cuando:

Entre 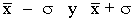se encuentra aproximadamente el 68% de los datos.
Entre 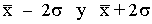se encuentra aproximadamente el 95% de los datos.
Entre 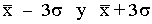se encuentra el 99% de los datos.

Un dato es atípico cuando está fuera de estos intervalos.

Ejemplo 1:

Los jugadores de un determinado equipo de baloncesto se clasifican por alturas según la
tabla siguiente:

Altura	[1,70 , 1,75)	[1,75 , 1,80)	[1,80 , 1,85)	[1,85 , 1,90)	[1,90 , 1,95)	[1,95 , 2,00)
Nº de jugadores	1	3	4	8	5	2

¿Cuántos valores hay en los intervalos () , () y ()? Estudia la concentración de los datos.

Altura
[1,70 , 1,75)	1,725	1	2,976	1,725	2,976
[1,75 , 1,80)	1,775	3	3,151	5,325	9,453
[1,80 , 1,85)	1,825	4	3,331	7,3	13,324
[1,85 , 1,90)	1,875	8	3,516	15,0	28,128
[1,90 , 1,95)	1,925	5	3,706	9,625	18,53
[1,95 , 2,00)	1,975	2	3,901	3,95	7,802
Sumatorio	11,1	23	20,578	42,925	80,213

Puntuaciones típicas o normalizadas

Para comparar datos correspondientes a dos distribuciones distintas, debemos tipificar (o normalizar) los valores.

y después comparar los resultados.

Las puntuaciones típicas (o puntuaciones z) tienen las siguientes propiedades:

Si se transforma una distribución en puntuaciones típicas, no varía la forma de la distribución
original.
La media aritmética de las puntuaciones normalizadas es cero, es decir:
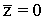
La desviación típica de las puntuaciones típicas es la unidad, es decir :

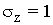
Ejemplo 2:

En una clase hay 20 alumnos y 15 alumnas. El peso medio de los 20 alumnos es de 64,7 kg y el de las 15 alumnas es de 57,3 kg. Supongamos que las desviaciones típicas de los dos grupos son, respectivamente, 4,2 kg y 5,7 kg. El peso de Luis es de 71 kg y el de Laura es de 62 kg. ¿Cuál de ellos puede, dentro del grupo de alumnos de su sexo, considerarse más grueso?