Ejercicios de representación de funciones logarítmicas
Representa gráficamente las siguientes funciones:
![]()
![]()
![]()
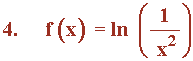
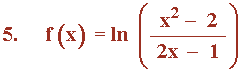
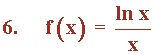
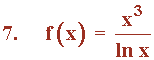
Resumen de las propiedades de la función logaritmo neperiano
| 1 | La función logarítmica es la inversa de la exponencial: y = Ln x ⇔ x = ey |
|---|---|
| 2 | La función y = Ln x tiene por dominio { x ∈ R | x > 0 } y por recorrido R . |
| 3 | La función y = Ln x es continua, creciente e inyectiva en todo su dominio. |
| 4 | La función y = Ln x es convexa o cóncava hacia abajo en todo su dominio. |
| 5 | |
Representa gráficamente la función: f(x) = ln (x + 1)
Función logarítmica.
Al tratarse de una función logarítmica, el dominio coincide con los valores donde está definido el logarítmo. En este caso está definido para x + 1 > 0 ⇒ x > - 1:
• Dom(f) = (-1, +∞)
Para hallar el recorrido de la función, invertimos las variables y calculamos el dominio de la variable y :
• Im(f) = R
Continuidad y tipos de discontinuidad
La función es continua en (0, +∞) .
• Corte con el eje OX: f(x) = 0
![]()
El punto de corte es: (0, 0)
• Corte con el eje OY: f(0)
f(0) = ln (0 + 1) = ln 1 = 0
El punto de corte es: (0, 0)
Como el puntos de corte con el eje OX es x = 0 , tenemos que estudiar los siguientes intervalos: (-∞, 0) , (0, +∞) :
| Intervalo | (-∞, 0) | (0, +∞) |
|---|---|---|
| Punto de prueba | f(-1) < 0 | f(1) > 0 |
| Signo de f (x) | - | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
f(- x) = ln (- x + 1) ≠ f(x) ⇒ No es par.
f(- x) = ln (- x + 1) ≠ -f(x) ⇒ No es impar.
Por lo tanto la función no es simétrica .
No es periódica porque las funciones logarítmicas nunca lo son.
Asíntotas
En este caso estudiamos el límite cuando x → -1+
![]()
Por lo tanto la función tiene una asíntota veritcal en x = -1 .
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
Por lo tanto la función no tiene asíntotas horizontales. No estudiamos el límite en menos infinito puesto que la función únicamente está definida para valores estrictamente positivos.
Para hallar las asíntotas oblicuas calculamos el siguiente límite:
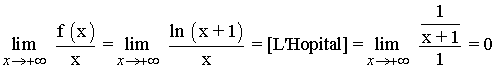
Por lo tanto la función no tiene asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
Es decir, no existe ningún valor que anule a la primera derivada.
Por lo tanto tenemos que estudiar el siguiente intervalo: (0, +∞)
| Intervalo | (0, +∞) |
|---|---|
| Punto de prueba | f ' (1) > 0 |
| Signo de f ' (x) | + |
| Monotonía | Crece |
Por el apartado anterior sabemos no existen puntos críticos o que anulen a la derivada primera, por lo tanto la función no tiene ni máximos ni níminos relativos.
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
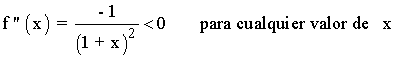
Por lo tanto ningún valor anula a la segunda derivada, por lo que únicamente estudiamos el intervalo donde está definida la función: (0, +∞)
| Intervalo | (0, +∞) |
|---|---|
| Punto de prueba | f '' (1) < 0 |
| Signo de f '' (x) | - |
| Curvatura | Convexa (∩) |
Punto de inflexión
Por el apartado anterior sabemos que no existe ningún punto que anule a la derivada segunda, por lo tanto la función no tiene puntos de inflexión.
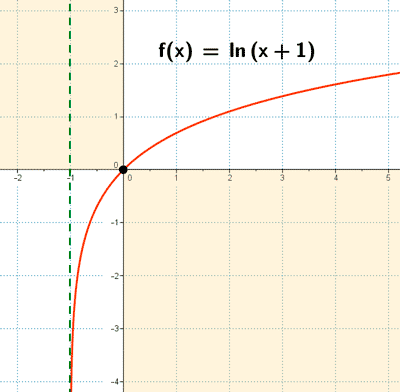
Representa gráficamente la función: f(x) = ex + Ln x
a) Estudiar las asíntotas de f(x)
b) Estudiar la monotonía de f(x)
c) Deducir que f(x) presenta un punto de inflexión
Función exponencial logarítmica.
Al tratarse de una función exponencial logarítmica, el dominio coincide con los valores donde está definido el logarítmo. En este caso está definido para x > 0:
• Dom(f) = (0, +∞)
Para hallar el recorrido de la función, invertimos las variables y calculamos el dominio de la variable y :
• Im(f) = R
Continuidad y tipos de discontinuidad
La función es continua en (0, +∞) .
Asíntotas
Nuestra función se puede escribir de la siguiente forma:
![]()
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
Para hallar las asíntotas oblicuas calculamos el siguiente límite:
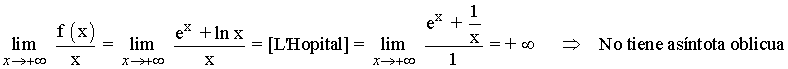
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
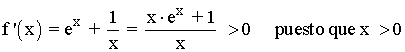
Por lo tanto la función es creciente en (0, +∞)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
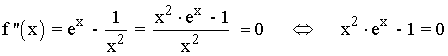
Para demostrar que la anterior ecuación tiene una solución, utilizamos el teorema de Bolzano para: g(x) = x2·ex - 1
La función g(x) es continua y derivable en el intervalo (0, 1) y además tenemos que:
• g(0) = -1 < 0
• g(1) = e - 1 > 0
Por el teorema de Bolzano existe un punto c ∈ (0, 1) tal que g(c) = 0
Punto de inflexión
Por el apartado anterior sabemos que existe un punto c que anula a la segunda derivada.
Vamos a determinar a través de la tercera derivada si se trata de puntos de inflexión:
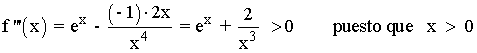
Por lo tanto, en x = c existe un punto de inflexión.
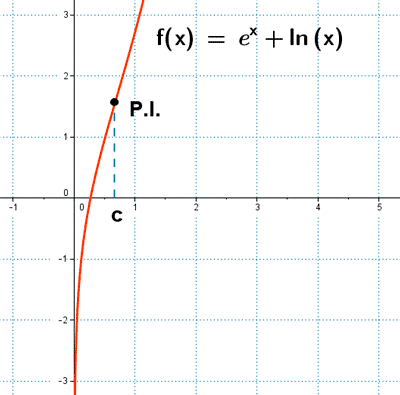
Representa gráficamente la función: f(x) = - x Ln x
Función logarítmica.
Al tratarse de una función logarítmica, el dominio coincide con los valores donde está definido el logarítmo. En este caso está definido para x > 0:
• Dom(f) = (0, +∞)
Para hallar el recorrido de la función, invertimos las variables y calculamos el dominio de la variable y :
• Im(f) = (-∞, 1/e)
Continuidad y tipos de discontinuidad
La función es continua en (0, +∞) .
• Corte con el eje OX: f(x) = 0
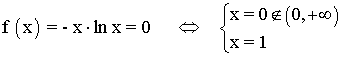
El punto de corte es: (1, 0)
• Corte con el eje OY: f(0)
La función no corta al eje OY puesto que no está definida en el punto x = 0
Como el puntos de corte con el eje OX es x = 0 , tenemos que estudiar los siguientes intervalos: (-∞, 0) , (0, +∞) :
| Intervalo | (0, 1) | (1, +∞) |
|---|---|---|
| Punto de prueba | f(1/2) > 0 | f(2) < 0 |
| Signo de f (x) | + | - |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
f(- x) = - (-x)·ln (- x) = x·ln (- x) ≠ f(x) ⇒ No es par.
f(- x) = - (- x)·ln (- x) = x·ln (- x) ≠ -f(x) ⇒ No es impar.
Por lo tanto la función no es simétrica .
No es periódica porque las funciones logarítmicas nunca lo son.
Asíntotas
En este caso estudiamos el límite cuando x → 0+
![]()
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
Por lo tanto la función no tiene asíntotas horizontales. No estudiamos el límite en menos infinito puesto que la función únicamente está definida para valores estrictamente positivos.
Para hallar las asíntotas oblicuas calculamos el siguiente límite:
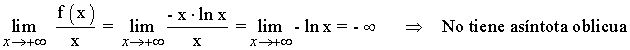
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
Es decir, no existe ningún valor que anule a la primera derivada.
Por lo tanto tenemos que estudiar el siguiente intervalo: (0, 1/e) y (1/e, +∞)
| Intervalo | (0, 1/e) | (1/e, +∞) |
|---|---|---|
| Punto de prueba | f ' (1/2e) > 0 | f ' (1) > 0 |
| Signo de f ' (x) | + | - |
| Monotonía | Crece | Decrece |
Por el apartado anterior sabemos que el punto crítico o punto que anula a la derivada primera es x = 1/e , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda:
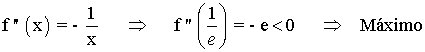
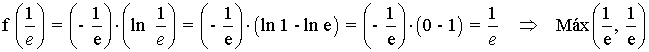
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
Por lo tanto ningún valor anula a la segunda derivada, por lo que únicamente estudiamos el intervalo donde está definida la función: (0, +∞)
| Intervalo | (0, +∞) |
|---|---|
| Punto de prueba | f '' (1) < 0 |
| Signo de f '' (x) | - |
| Curvatura | Convexa (∩) |
Punto de inflexión
Por el apartado anterior sabemos que no existe ningún punto que anule a la derivada segunda, por lo tanto la función no tiene puntos de inflexión.
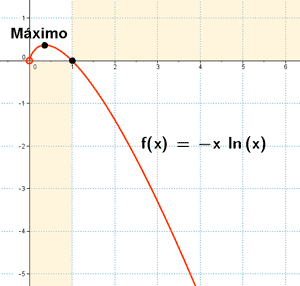
Representa gráficamente la función:
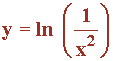
Función logarítmica.
Al tratarse de una función logarítmica tenemos que estudiar los valores que sean mayores que 0 y además los valores que anulan al denominador al ser racional:
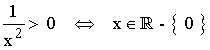
Al estar el denominador elevado al cuadrado, cualquier número menos el 0 cumple la condición:
• Dom(f) = R - {0} = (-∞, 0) ∪ (0, +∞)
Para hallar el recorrido de la función, invertimos las variables y calculamos el dominio de la variable y :
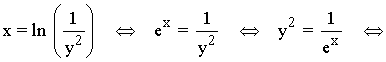
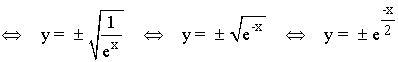
• Im(f) = R = (-∞, +∞)
Continuidad y tipos de discontinuidad
La función es continua en R - {0} , es decir, es discontinua en el punto x = 0
• Corte con el eje OX: f(x) = 0
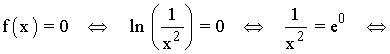
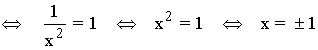
Los puntos de corte son: (-1, 0) y (1, 0)
• Corte con el eje OY: f(0)
La función no está definida en x = 0 , por lo tanto la función no corta al eje OY.
Como los puntos de corte con el eje OX son x = -1 y x = 1 y además la función es discontinua en el punto x = 0 , tenemos que estudiar los siguientes intervalos: (-∞, -1) , (-1, 0) , (0, 1) y (1, +∞) :
| Intervalo | (-∞, -1) | (-1, 0) | (0, 1) | (1, +∞) |
|---|---|---|---|---|
| Punto de prueba | f(-3) < 0 | f(-0,5) > 0 | f(0,5) > 0 | f(3) < 0 |
| Signo de f (x) | - | + | + | - |
En la gráfica se marcan los puntos de corte con los ejes, los puntos de distintinuidad y las regiones donde no hay curva.
![]()
Por lo tanto la función es simétrica respecto al eje OY .
No es periódica porque las funciones logarítmicas nunca lo son.
Asíntotas
Donde se anula la característica del logarítmo:
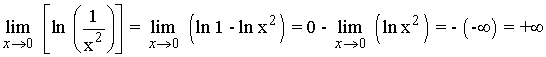
Por las características del logarítmo, sabemos que:
![]()
Es decir, existe una asíntota vertical en x = 0 .
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
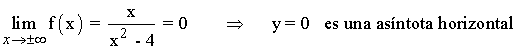
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
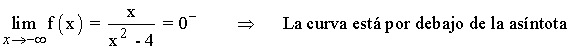
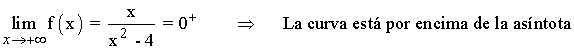
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
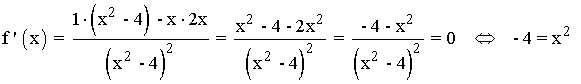
El numerador de la primera derivada no se anula para ningún valor, puesto que x2 ≠ -4 para cualquier valor de x .
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad sin incluir ninguno más puesto que no hay ningún valor que anule a la derivada primera: (-∞, -2) , (-2, 0) , (0, 2) , (2, +∞)
| Intervalo | (-∞, -2) | (-2, 0) | (0, 2) | (2, +∞) |
|---|---|---|---|---|
| Punto de prueba | f ' (-3) < 0 | f ' (-1) < 0 | f ' (1) < 0 | f ' (3) < 0 |
| Signo de f ' (x) | - | - | - | - |
| Monotonía | Decrece | Decrece | Decrece | Decrece |
Por el apartado anterior sabemos que ningún valor anula a la primera derivada, por lo tanto la función no tiene puntos críticos. Es decir, la función no tiene máximos ni mínimos.
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
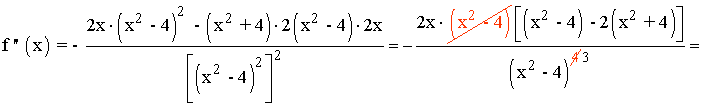
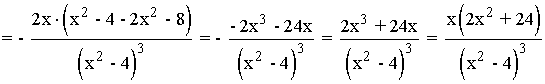
La segunda derivada se anula para x = 0 y 2x2 + 24 = 0
La segunda ecuación no tiene solución real, por lo tanto la segunda derivada solamente se anula para x = 0 .
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad incluyendo el valor que anula a la segunda derivada: (-∞, -2) , (-2, 0) , (0, 2) , (2, +∞)
| Intervalo | (-∞, -2) | (-2, 0) | (0, 2) | (0, +∞) |
|---|---|---|---|---|
| Punto de prueba | f '' (-3) < 0 | f '' (-1) > 0 | f '' (1) < 0 | f '' (3) > 0 |
| Signo de f '' (x) | - | + | - | + |
| Curvatura | Convexa (∩) | Concava (∪) | Convexa (∩) | Concava (∪) |
Punto de inflexión
Por el apartado anterior sabemos que el punto que anula a la derivada segunda es x = 0 y vamos a determinar a través de la tercera derivada si se trata de un punto de inflexión.
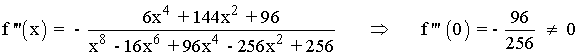
Por lo tanto x = 0 es la abscisa del punto de inflexión ⇒ f(0) = 0 ⇒ Punto inflexión (0, 0)
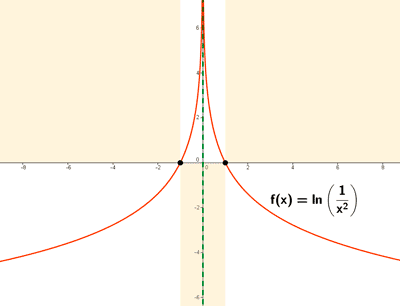
Sea la función:
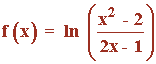
a) Dominio, cortes de los ejes y asíntotas
b) Intervalos de crecimiento y decrecimiento
c) A partir de los datos obtenidos representar gráficamente la función
Función logarítmica.
Al tratarse de una función logarítmica, el dominio coincide con los valores donde está definido el logarítmo, es decir, para los valores mayores de 0. En este caso está definido para:

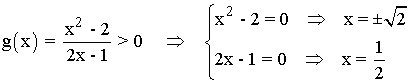
| Intervalo | (-∞, -√2) | (-√2, 1/2) | (1/2, +√2) | (+√2, +∞) |
|---|---|---|---|---|
| Punto de prueba | g(-3) < 0 | g(0) > 0 | g(1) < 0 | f(3) > 0 |
| Signo de g (x) | - | + | - | + |
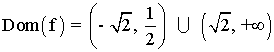
Para hallar el recorrido de la función, invertimos las variables y calculamos el dominio de la variable y :
Im(f) = R
Continuidad y tipos de discontinuidad
La función es discontinua en los intervalos (-∞, -√2] ∪ [1/2, √2].
• Corte con el eje OX: f(x) = 0
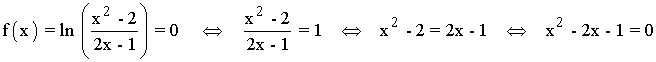
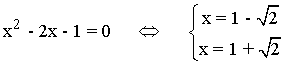
El punto de corte es: (1 - √2, 0) y (1 - √2, 0)
• Corte con el eje OY: f(0)
f(0) = ln 2 ⇒ El punto de corte con el eje OY es (0, ln 2)
Para estudiar los intervalos de signo constante debemos tener en cuenta el dominio de la función y los puntos de corte, es decir, tenemos que estudiar los siguientes intervalos: (-∞, 0) , (0, +∞) :
| Intervalo | (-√2, 1 - √2) | (1 - √2, 1/2) | ( √2, 1 + √2) | (1 + √2, +∞) |
|---|---|---|---|---|
| Punto de prueba | f(-1) < 0 | f(0) > 0 | f(2) < 0 | f(4) > 0 |
| Signo de f (x) | - | + | - | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
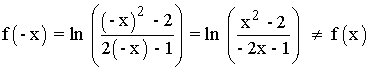
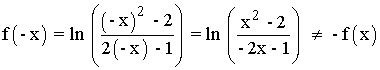
Por lo tanto la función no es simétrica .
No es periódica porque las funciones logarítmicas nunca lo son.
Asíntotas
En este caso estudiamos el límite cuando x → 0+
![]()
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
Por lo tanto la función no tiene asíntotas horizontales. No estudiamos el límite en menos infinito puesto que la función únicamente está definida para valores estrictamente positivos.
Para hallar las asíntotas oblicuas calculamos el siguiente límite:
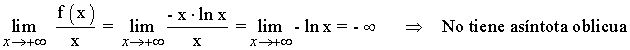
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
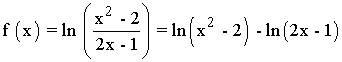
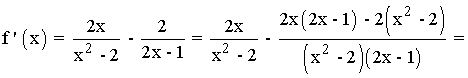
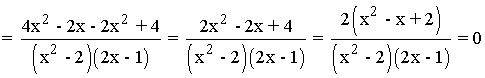
Es decir, la primera derivada se anula cuando x2 - x + 2 = 0
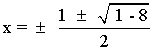
La ecuación anterior no tiene raíces reales, por lo que no existe ningún valor que anule a la primera derivada.
Por lo tanto, estudiamos los intervalos de continuidad: (-√2, 1/2) y +√2, +∞)
| Intervalo | (-√2, 1/2) | (+√2, +∞) |
|---|---|---|
| Punto de prueba | f ' (0) > 0 | f ' (2) > 0 |
| Signo de f ' (x) | + | + |
| Monotonía | Crece | Crece |
Por el apartado anterior sabemos que la primera derivada no se anula en ningún punto, por lo que la función no tiene ni máximos ni mínimos.
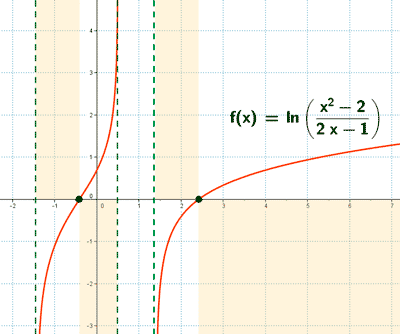
Sea la función:
![]()
a) Representar la función
b) Hallar la ecuación de la recta tangente en el punto de inflexión
c) Dibuja la recta tangente en el punto de inflexión
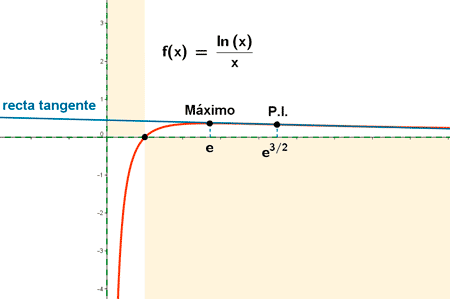
Función logarítmica.
Al tratarse de una función logarítmica, el dominio coincide con los valores donde está definido el logarítmo, es decir, para los valores mayores de 0. En este caso está definido para:
Dom (f) = { x∈R tales que x > 0 } = (0, +∞)
Para hallar el recorrido de la función, invertimos las variables y calculamos el dominio de la variable y :
Im(f) = (-∞, 1/e)
Continuidad y tipos de discontinuidad
La función es discontinua en los intervalos (0, +∞).
• Corte con el eje OX: f(x) = 0
![]()
El punto de corte es: (1, 0)
• Corte con el eje OY: f(0)
La función no está definida para x = 0 por lo tanto la función no corta al eje OY.
Para estudiar los intervalos de signo constante debemos tener en cuenta el dominio de la función y los puntos de corte, es decir, tenemos que estudiar los siguientes intervalos: (0, 1) , (1, +∞) :
| Intervalo | (0, 1) | (1, +∞) |
|---|---|---|
| Punto de prueba | f(0,5) < 0 | f(2) > 0 |
| Signo de f (x) | - | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
![]()
![]()
Por lo tanto la función no es simétrica .
No es periódica porque las funciones logarítmicas nunca lo son.
Asíntotas
En este caso estudiamos el límite cuando x → 0+
![]()
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
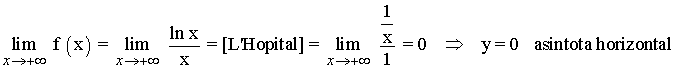
Por lo tanto la función no tiene asíntotas horizontales. No estudiamos el límite en menos infinito puesto que la función únicamente está definida para valores estrictamente positivos.
La función no tiene asíntotas oblicuas porque ya tiene asíntota horizontal.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
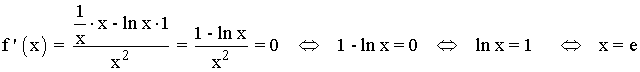
La ecuación anterior no tiene raíces reales, por lo que no existe ningún valor que anule a la primera derivada.
Por lo tanto, estudiamos los intervalos de continuidad: (-√2, 1/2) y +√2, +∞)
| Intervalo | (0, e) | (e, +∞) |
|---|---|---|
| Punto de prueba | f ' (0,5) > 0 | f ' (4) < 0 |
| Signo de f ' (x) | + | - |
| Monotonía | Crece | Decrece |
Por el apartado anterior sabemos que la primera derivada se anula en x = e .
Vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
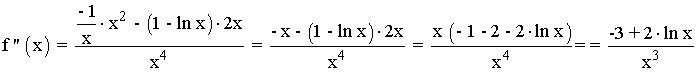
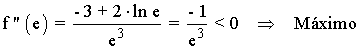
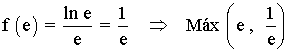
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
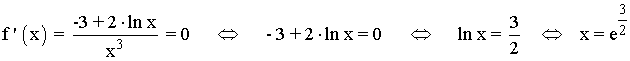
Por lo tanto tenemos que estudiar los siguientes intervalos: (0, e3/2) , (e3/2, +8)
| Intervalo | (0, e3/2) | (e3/2, +∞) |
|---|---|---|
| Punto de prueba | f '' (1) < 0 | f '' (5) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
Punto de inflexión
Por el apartado anterior sabemos que existe un punto que anula a la derivada segunda x = e3/2.
Para saber si es un punto de inflexión, hallamos la tercera derivada:
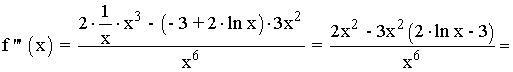
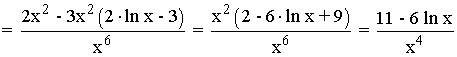
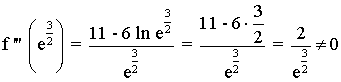
Por lo tanto en el punto x = e3/2 existe un punto de inflexión:
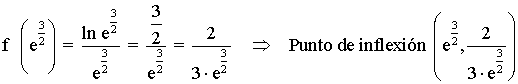
La ecuación de la recta tangente en el punto de inflexión es de la forma: y - f(e3/2) = f ' (e3/2) ·(x - e3/2)
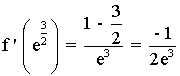
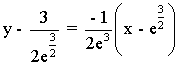
Sea la función:
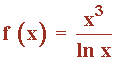
a) Estudiar el dominio de la función
b) Hallar las asíntotas de la función
c) Estudiar los intervalos de crecimiento y decrecimiento
d) Estudiar los extremos relativos
e) Representar gráficamente
Función logarítmica.
Al tratarse de una función logarítmica, el dominio coincide con los valores donde está definido el logarítmo. En este caso está definido para x > 0 . Además, el denominador de la función se anula cuando ln x = 0 es decir, cuando x = 1
• Dom(f) = (0, 1) ∪ (1, +∞)
Continuidad y tipos de discontinuidad
La función es continua en (0, +∞) .
Asíntotas
El denominador de la función se anula en x = 1 por lo que tenemos que hallar los límites laterales:
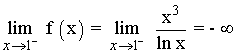
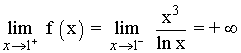
Por lo tanto x = 1 es una asíntota vertical.
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
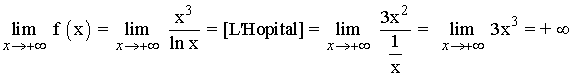
Por lo tanto la función no tiene asíntotas horizontales. No estudiamos el límite en menos infinito puesto que la función no está definida para valores negativos.
Para hallar las asíntotas oblicuas calculamos el siguiente límite:
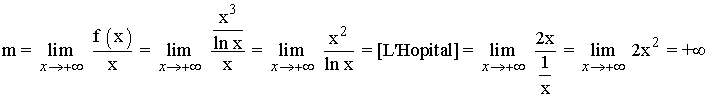
Por lo tanto la función no tiene asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
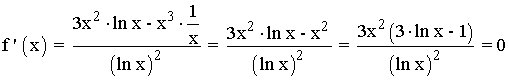
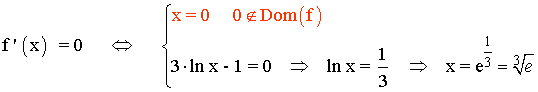
Por lo tanto tenemos que estudiar el siguiente intervalo: (0, 1) , (1, 3√e) y (3√e, +∞)
| Intervalo | (0, 1) | (1, 3√e) | (3√e, +∞) |
|---|---|---|---|
| Punto de prueba | f ' (0,5) < 0 | f ' (1,1) < 0 | f ' (3) > 0 |
| Signo de f ' (x) | - | - | + |
| Monotonía | Decrece | Decrece | Crece |
Por el apartado anterior sabemos que el punto crítico o punto que anula a la derivada primera es: x = 3√e
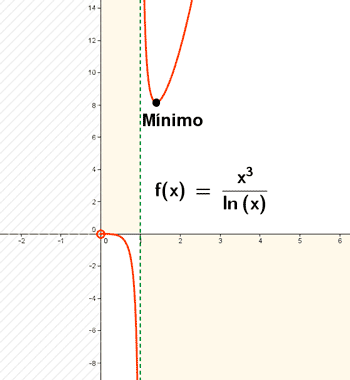
Como la función es creciente en el intervalo (1, 3√e) y decreciente en el intervalo (3√e, +∞)) , la función presenta un mínimo relativo:
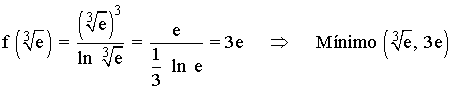


 INICIO
INICIO