Dominio y recorrido de una función
Dada una función real de variable real:
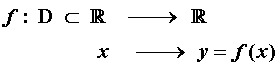
El dominio de la función es el conjunto D ⊂ R de los valores para los que está definida la función. Se representa por Dom f.
![]()
El recorrido o imagen de la función es el conjunto de valores que toma la función. Se representa por Im f.
![]()
Ejemplo de dominio y recorrido de una función
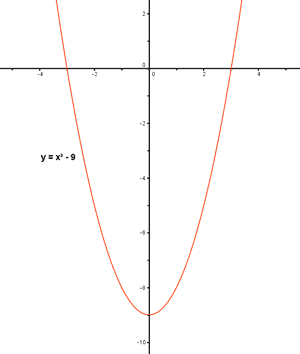
Sea la función f(x) = x2 - 9
La expresión f(x) = x2 - 9 tiene sentido para todo x .
Por lo tanto, Dom(f) = R.
Los valores que toma f(x) son siempre mayores o iguales que - 9 .
Es decir Im(f) = [- 9, +∞)

Calcular el dominio de una función
Funciones polinómicas
El dominio es R ya que para todo valor real de la variable x puede calcularse el correspondiente valor y .
Son ejemplos de funciones polinómicas:
f(x) = x g(x) = 3x - 2 h(x) = x2 - 3x + 5 q(x) = x4 - 3x2 + 8
Dom(f) = R Dom(g) = R Dom(h) = R Dom(q) = R
Funciones racionales
El dominio está formado por todos los números reales, excepto por aquellos que anulan el denominador.
Son ejemplos de funciones racionales:
![]()
El denominador de f se anula cuando x - 2 = 0 , es decir, x = 2 . Por lo tanto, Dom(f) = R - {2}
El denominador de g se anula cuando x2 - 9 = 0 , es decir, x = ± 3 . Por lo tanto, Dom(g) = R - {- 3, 3}
El denominador de h se anula cuando 5 - x = 0 , es decir, x = 5 . Por lo tanto, Dom(h) = R - {5}
Funciones irracionales
Para determinar el dominio de una función irracional existen dos casos:
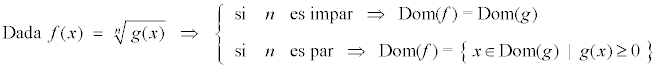
Son ejemplos de funciones irracionales:
![]()
La función f tiene sentido, al ser n par, cuando x - 5 ≥ 0 , es decir, x ≥ 5 . Por lo tanto, Dom(f) = [5, + ∞)
La función h tiene el mismo dominio, al ser n impar, que la función x2 - 5 . Por lo tanto, Dom(h) = R
Funciones exponenciales
El dominio de una función exponencial es igual al dominio de la función que aparezca en el exponente.
![]()
Son ejemplos de funciones exponenciales:

La función f tiene el mismo dominio que la función x2 - 5 . Por lo tanto, Dom(f) = R
La función h no tiene sentido cuando se anula el denominador del exponente, x - 7 = 0 , es decir x = 7 . Por lo tanto, Dom(h) = R - {7}
Funciones logarítmicas
Debido a que solo tienen sentido los logaritmos de números positivos, resulta que:
![]()
Son ejemplos de funciones logarítmicas:
![]()
Para f(x) resolvemos la inecuación x - 3 > 0 , es decir x > 3 . Por lo tanto, Dom(f) = (- ∞, 3)
Para h(x) resolvemos la inecuación x2 - 4 > 0 , es decir (x + 2)(x - 2) > 0
Para x = - 3 tenemos que (- 3)2 - 4 = 9 - 4 = 5 > 0 .
Para x = 0 tenemos que 02 - 4 = - 4 < 0 .
Para x = 3 tenemos que 32 - 4 = 9 - 4 = 5 > 0 .
Por lo tanto, Dom(h) = (- ∞, - 2) ∪ (2, +∞)
Dominio y recorrido de las funciones trigonométricas
Calcular el recorrido de una función
Para hallar el recorrido de una función f(x) hacemos lo siguiente:
1. Igualamos f(x) = y
2. Despejamos la variable x.
3. Estudiamos el dominio de la nueva función.
Ejemplo de recorrido de una función.
Vamos a hallar el recorrido de la función:
![]()
Calculamos su dominio:
3 - x = 0 ⇔ x = 3 ⇒ Dom(f) = R - {3}
Hacemos f(x) = y , y despejamos x:
![]()
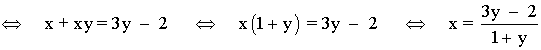
No son del recorrido de f los siguientes valores de y:
• Los que no permiten calcular x, es decir: 1 + y = 0 ⇔ y = - 1
• Los que darían como resultado x = 3:
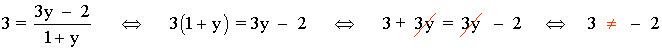
No hay ningún valor de y para el que x tenga valor 3.
Por tanto: Im(f) = R - {-1}


 INICIO
INICIO

