Continuidad de una función
Una función es continua en un punto a si se cumplen las tres condiciones siguientes:
1) Existe el límite de f(x) cuando x tiende a a .
2) La función está definida en el punto a .
3) Los dos valores anteriores coinciden.
![]()
Una función es continua en un intervalo si es continua en todos los puntos del intervalo.
De la misma forma, una función es continua en todo su dominio cuando lo es en todos los puntos que componen su dominio.
Continuidad de las funciones elementales
Una función polinómica f(x) = a0 + a1x + ... + anxn es continua en todo punto de R .
Una función racional f(x) = P(x) / Q(x) donde P(x) y Q(x) son polinomios, es continua en todo R excepto aquellos puntos que anulen el denominador.
Una función radical o irracional f(x) = √g(x) es continua en todo R si n es impar y en los puntos donde g(x) ≥ 0 si n es par .
Una función exponencial f(x) = ax (donde a > 0 y a ≠ 1 ) es continua en todo R .
Una función logarítmica f(x) = loga x (donde a > 0 y a ≠ 1 ) es continua en el intervalo (0, +∞) .
Las funciones trigonométricas f(x) = sen x y f(x) = cos x son continuas en todo R .
La función trigonométrica f(x) = tg x es continua en todo R excepto en los puntos de la forma x = (π/2) + k·π .
Ejemplo del cálculo de la continuidad de una función:
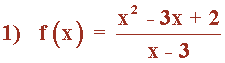
Al tratarse de una función racional, estudiamos los puntos donde la función no está definida.
Esto ocurre cuando se anula el denominador, es decir, cuando x - 3 = 0 ⇒ x = 3 .
Por lo tanto la función es continua en: R - {3} .
![]()
La función f(x) es una función irracional. Por lo tanto estudiamos cuando x2 - 9 ≥ 0 .
x2 - 9 ⇒ (x - 3)(x + 3) ≥ 0 ⇒ Las raíces son x = - 3 y x = 3 .
Estudiamos el signo en los siguientes tres intervalos:
• A = (-∞, -3) ⇒ f(-4) = √7 > 0 .
• B = (-3, 3) ⇒ f(0) = √-9 No existe .
• C = (3, +∞) ⇒ f(4) = √7 > 0 .
Por lo tanto la función es continua en: (-∞, -4] ∪ [4, +∞) .
![]()
La función f(x) es una función logarítmica. Por lo tanto estudiamos cuando 1 - x2 > 0 .
1 - x2 ⇒ (1 - x)(1 + x) > 0 ⇒ Las raíces son x = -1 y x = 1
Estudiamos el signo en los siguientes tres intervalos:
• A = (-∞, -1) ⇒ f(-2) = ln (-3) No existe .
• B = (- 1, 1) ⇒ f(0) = ln 1 > 0 .
• C = (1, +∞) ⇒ f(2) = ln (-3) No existe .
Por lo tanto la función es continua en: (-1, 1) .


 INICIO
INICIO
