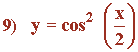Ejercicios de representación de funciones trigonométricas II
Representa las siguientes funciones trigonométricas:
1) y = sen x cos x
2) y = x - 2 sen x
3) y = 2 cos x - cos 2x
4) y = 3 sen x - sen 3x
6) f(x) = ex sen x
7) f(x) = x - arc tg x
8) y = sen2 x
10) y = cos2x + cos x
Funciones trigonométricas: periodo, amplitud, asíntotas verticales, dominio e imagen.
| Periodo | Amplitud | Asintotas verticales |
Dominio | Imagen | |
|---|---|---|---|---|---|
| y = sen x | 2π | 1 | No tiene | R | { y∈R | -1 ≤ y ≤ 1 } |
| y = cos x | 2π | 1 | No tiene | R | { y∈R | -1 ≤ y ≤ 1 } |
| y = tg x | π | π/2 (2k + 1) , k∈Z | { x∈R | x ≠ π/2 (2k + 1) } | R | |
| y = cotg x | π | k·π , k∈Z | { x∈R | x ≠k·π } | R | |
| y = sec x | 2π | π/2 (2k + 1) , k∈Z | { x∈R | x ≠ π/2 (2k + 1) } | { y∈R | y ≤ -1 ó y ≥ 1 } | |
| y = cosec x | 2π | k π , k∈Z | { x∈R | x ≠k·π } | { y∈R | y ≤ -1 ó y ≥ 1 } |
Representa gráficamente la función: y = sen x cos x
Aplicando la fórmula trigonométrica del ángulo doble tenemos que:
![]()
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) : [-1/2 , 1/2]
La función seno es periódica de periodo 2π, luego:
![]()
Luego nuestra función es periódica de periodo π .
Por tanto, haremos el estudio de la función en el intervalo: [0 , π)
Continuidad y tipos de discontinuidad
La función es continua en todo su dominio.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
![]()
Puntos de corte con el eje X:
![]()
![]()
Como los puntos de corte con el eje OX son x = π/2 y x = 0 , y el período de la función es [0 , π ) , estudiaremos el signo en los intervalos: (0, π/2) , (π/2 , π)
| Intervalo | (0, π/2) | (π/2 , π) |
|---|---|---|
| Punto de prueba | f(π/4) > 0 | f(2π/3) < 0 |
| Signo de f (x) | + | - |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
![]()
sen(-x) = - sen x
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '(x) = 1/2 · 2 · cos (2x) = cos (2x) = 0 ⇔ 2x = π/2 ó 2x = 3π/2 ⇔ x = π/4 ó x = 3π/4
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (0, π/4) , (π/4, 3π/4) , (3π/4, π)
| Intervalo | (0 , π/4) | (π/4 , 3π/4) | (3π/4 , π) |
|---|---|---|---|
| Punto de prueba | f ' ( π/6) > 0 | f ' (π/2) < 0 | f ' (7 π/8) > 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = π/4 y x = 3π/4 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = 2 (- sen 2x) = - 2 sen(2x)
• f '' ( π/4) = - 2 < 0 ⇒ Hay un máximo en x = π/4 ⇒ f(π/4) = 1/2 ⇒ Max (π/4, 1/2)
• f '' (3π/4) = 2 > 0 ⇒ Hay un mínimo en x = 3π/4 ⇒ f(3π/4) = - 1/2 ⇒ Min (3π/4, -1/2)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
f '' (x) = - 2 sen(2x) = 0 ⇒ sen(2x) = 0 ⇒ 2x = 0 ó 2x = π ⇒ x = 0 , x = π/2
Tenemos que estudiar los siguientes intervalos: (0, π/2) , ( π/2, π)
| Intervalo | (0, π/2) | ( π/2, π) |
|---|---|---|
| Punto de prueba | f '' ( π/4) < 0 | f '' ( 3π/4) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente cóncava en ( π/2, π) y cóncava hacia abajo o convexa en (0, π/2) .
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = 0 , x = π/2 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f ''' (x) = - 2·2·cos (2x) = - 4 cos (2x)
f ''' (0) = - 4 ≠ 0 ⇒ x = 0 es la abscisa del punto de inflexión ⇒ f(0) = 0 ⇒ Punto inflexión (0, 0)
f ''' (π/2) = 4 ≠ 0 ⇒ x = π/2 es la abscisa del punto de inflexión ⇒ f(π/2) = 0 ⇒ Punto inflexión ( π/2, 0)
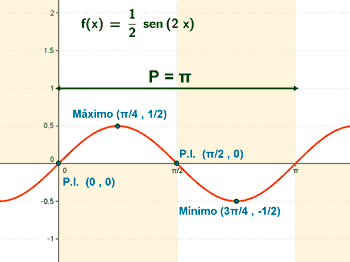
Representar gráficamente la función f(x) = x - 2 sen x en el intervalo - π < x < π , determinando sus extremos (máximos y mínimos relativos), crecimiento, decrecimiento , curvatura y puntos de inflexión.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
f ' (x) = 1 - 2 cos x= 0 ⇒ cos (x) = 1/2 ⇒ x = π/3 , x = -π/3
Tenemos que estudiar la monotonía en los intervalos: (-π , -π/3) , (-π/3, π/3) , (π/3 , π)
| Intervalo | (-π , -π/3) | (-π/3, π/3) | (π/3 , π) |
|---|---|---|---|
| Punto de prueba | f ' ( -π/2) > 0 | f ' (0) < 0 | f ' (π/2) > 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = π/3 y x = -π/3 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = 2 sen x
• f '' (π/3) = √3 > 0 ⇒ Hay un mínimo en x = π/3 ⇒ f(π/3) = π/3 - √3 ⇒ Min (π/3 , π/3 - √3)
• f '' (-π/3) = -√3 < 0 ⇒ Hay un máximo en x =-π/3 ⇒ f(-π/3) = -π/3 - √3 ⇒ Min (-π/3 , -π/3 + √3)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = 2 sen x = 0 ⇒ x = 0
Tenemos que estudiar los siguientes intervalos: (-π, 0) , ( 0, π)
| Intervalo | (-π , 0) | ( 0 , π) |
|---|---|---|
| Punto de prueba | f '' (- π/2) < 0 | f '' ( π/2) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente concava en ( 0, π) y concava hacia abajo o convexa en (-π , 0) .
Punto de inflexión
Por el apartado anterior sabemos que el único punto que anula a la derivada segunda es x = 0 y vamos a determinar a través de la tercera derivada si se trata de un punto de inflexión.
f ''' (x) = 2 cos x
f ''' (0) = 2 ≠ 0 ⇒ x = 0 es la abscisa del punto de inflexión ⇒ f(0) = 0 ⇒ Punto inflexión ( 0, 0)
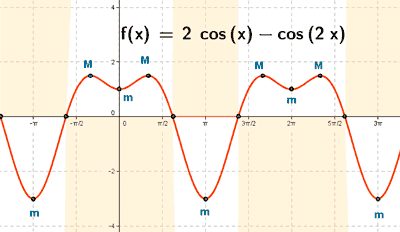
Representa gráficamente la función: y = 2 cos x - cos 2x
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) : [ -3 , 3/2 ]
La función coseno es periódica de periodo 2π , la función cos (2x) es periódica de periodo π .
La función diferencia y = 2 cos x - cos 2x es periódica con periodo 2π .
Estudiamos la función en el intervalo [0 , 2π] .
Continuidad y tipos de discontinuidad
La función es continua en todo su dominio.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 2 cos 0 - cos 0 = 2·1 - 1 = 1 ⇒ (0 , 1)
Puntos de corte con el eje X:
Si y = 0 ⇒ 2 cos x - cos 2x = 0
Aplicamos la fórmula de reducción de la potencia del coseno:
![]()
2 cos x - cos 2x = 0 ⇒ 2 cos x - ( 2cos2x - 1 ) = 0 ⇒ 2cos2 x - 2 cos x - 1 = 0
O bien aplicamos la fórmula del coseno del ángulo doble:
cos 2x = cos2 x - sen2 x
2 cos x - cos 2x = 0 ⇒ 2 cos x - (cos2 x - sen2 x) = 0 ⇒ 2 cos x - cos2 x + sen2 x = 0
2 cos x - cos2 x + (1 - cos2 x ) = 0 ⇒ 2 cos x - cos2x + 1 - cos2 x = 0 ⇒ 2 cos2 x - 2 cos x - 1 = 0
Resolvemos la ecuación de segundo grado (ahora la incógnita es 'cos x' ) :
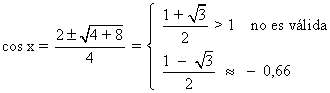
La primera solución la descartamos, ya que el coseno nunca puede ser mayor que 1. Nos quedamos con la segunda solución y aplicamos la función inversa del coseno:
cos x = - 0,66 ⇒ x = arc sen (-0,66) ⇒ x = 2,29 ⇒ (2,29 , 0)
x = 2,29 + π = 5,43
Los puntos de corte con el eje OX en el primer periodo son: (2,29 , 0) , (5,43 , 0)
Sabemos que la función coseno es par, es decir, cos(-x) = cos (x). Por tanto nuestra función tiene simetría par.
f(-x) = 2 cos (-x) - cos(-2x) = 2 cos x - cos (2x) = f(x)
Como la función es par, bastará con estudiarla en el intervalo [0 , 2π] .
Como el punto de corte con el eje OX es x = 2,29 , x = 5,43 , y el período de la función es [0 , 2π] , estudiaremos el signo en los intervalos: (0, 2,29) , (2,29 , 5,43) , (5,43 , 2π)
| Intervalo | (0, 2,29) | (2,29 , 5,43) | (5,43 , 2π) |
|---|---|---|---|
| Punto de prueba | f(π/2) > 0 | f(π) < 0 | f(3π/2) > 0 |
| Signo de f (x) | + | - | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
![]()
Aplicamos la fórmula del seno del ángulo doble: sen 2x = 2 sen x cos x
- sen x + sen 2x = 0 ⇒ - sen x + 2 sen x cos x = 0 ⇒ sen x ( - 1 + 2 cos x) = 0
La ecuación será 0 si: sen x = 0 ó - 1 + 2 cos x = 0
sen x = 0 ⇒ x = 0 , x = π , x = 2π
- 1 + 2 cos x = 0 ⇒ cos x = 1/2 ⇒ x = π/3 , x = - π/3 = 2π/3 + π/6 = 5π/3
Estudiaremos la monontonía en los intervalos: (0 , π/3) , (π/3 , π) , (π , 5π/3) , (5π/3 , 2π)
| Intervalo | (0 , π/3) | (π/3 , π) | (π , 5π/3) | (5π/3 , 2π) |
|---|---|---|---|---|
| Punto de prueba | f ' ( π/4) > 0 | f ' (3π/4) < 0 | f ' (7π/6) > 0 | f ' (11π/6) < 0 |
| Signo de f ' (x) | + | - | + | - |
| Monotonía | Crece | Decrece | Crece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 0 , x = π/3 , x = π , x = 5π/3 y x = 2π vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = - 2 cos x + 4 cos 2x
• f '' ( 0) = 2 > 0 ⇒ Hay un mínimo en x =0 ⇒ f(0) = 1 ⇒ Min (0, 1)
• f '' (π/3) = - 3 < 0 ⇒ Hay un máximo en x = π/3 ⇒ f(π/3) = 3/2 ⇒ Max (π/3, 3/2)
• f '' ( π) = 6 > 0 ⇒ Hay un mínimo en x = π ⇒ f(π) = - 3 ⇒ Max (π, - 3)
• f '' (5π/3) < 0 ⇒ Hay un máximo en x = 5π/3 ⇒ f(5π/3) = 3/2 ⇒ Max (5π/3, 3/2)
• f '' (2π) = 6 > 0 ⇒ Hay un mínimo en x = 2π ⇒ f(2π) = 1 ⇒ Max (2π, 1)
Representa gráficamente la función: y = 3 sen x - sen 3x
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) :
Por un lado: - 1 ≤ sen 3x ≤ 1
Multiplicamos por -1 : 1 ≥ - sen 3x ≥ 1
Reordenamos : -1 ≤ - sen 3x ≤ 1
Por otro: - 1 ≤ sen x ≤ 1
Multiplicamos por 3 : - 3 ≤ 3 sen x ≤ 3
Sumamos ambos resultados:
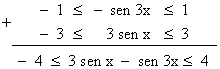
Im(f) = [-4 , 4]
La función seno es periódica de periodo 2π , luego:
sen (x) = sen (x + 2π) = sen (x + 4π) = sen (x + 6π) = ...
Por tanto:
f(x) = 3 sen x - sen 3x = 3 sen (x + 2π) - sen (3x + 6π) = 3 sen (x + 2π) - sen [3(x + 2π)] = f(x + 2π)
Luego nuestra función es periódica de periodo 2π .
Por tanto, haremos el estudio de la función en el intervalo: [0 , 2π]
Continuidad y tipos de discontinuidad
La función es continua en todo su dominio.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ f(0) = 3 sen 0 - sen 0 = 0 ⇒ (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 3 sen x - sen 3x
Vamos a encontrar una fórmula para sen 3x :
Como: 3x = x + 2x
Para calcular sen 3x aplicamos la fórmula del seno de una suma de ángulos:
sen(x + y) = sen x cos y + cos x sen y
sen 3x = sen (x + 2x) = sen x cos 2x + cos x sen 2x
Aplicamos las fórmulas del seno y del coseno del ángulo doble:
cos 2x = cos2x - sen2x , sen 2x = 2 sen x cos x
sen 3x = sen x cos 2x + cos x sen 2x = sen x [cos2x - sen2x] + cos x [2 sen x cos x] =
= sen x cos2 x - sen3 x + 2 sen x cos2x = 3 sen x cos2x - sen3x
Luego: sen 3x = 3 sen x cos2x - sen3x
Ahora sustituimos en nuestra ecuación y simplificamos:
3 sen x - sen 3x = 0 ⇒ 3 sen x - [ 3 sen x cos2x - sen3x ] = 0
3 sen x - 3 sen x cos2x + sen3x = 0 ⇒ sen x [ 3 - 3 cos2x + sen2x ] = 0
sen x [ 3 - 3 (1 - sen2x) + sen2x ] = 0 ⇒ sen x [ 3 - 3 + 3 sen2x + sen2x ] = 0
sen x [ 4 sen2x ] = 0 ⇒ 4 sen3x = 0
Resolvemos la ecuación:
4 sen3x = 0 ⇒ sen x = 0 ⇒ x = 0 , x = π , x = 2π
Luego los puntos de corte con el eje OX son: (0 , 0) , (π , 0) , (2π , 0)
f(-x) = 3 sen(-x) - sen (-3x) = - 3 sen x - (- sen 3x) = - 3 sen x + sen 3x = - f(x)
sen(-x) = - sen x
La función tiene simetría impar.
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '(x) = 3 cos x - 3 cos 3x
f ' (x) = 3 cos x - 3 cos 3x = 0 ⇒ 3 cos x = 3 cos 3x ⇒ cos x = cos 3x
Dos ángulos α y β tendrán el mismo coseno si están los cuadrantes:
• primero y cuarto: α = β + 2kπ , k∈Z
• segundo y tercero: α = - β + 2kπ , k∈Z
En nuestro caso:
• 3x = x + 2kπ , k∈Z ⇒ 2x = 2kπ , k∈Z ⇒ x = kπ , k∈Z
• 3x = - x + 2kπ , k∈Z ⇒ 4x = 2kπ , k∈Z ⇒ x = kπ/2 , k∈Z
Veamos qué puntos están dentro del primer periodo de la función [0 , 2π] :
• k = 0 : x = 0
• k = 1 : x = π , x = π/2
• k = 2 : x = 2π , x = π
• k = 3 : x = 3π , x = 3π/2
Por tanto, los puntos que anulan la primera derivada son:
x = 0 , x = π/2 , x = π , x = 3π/2 , x = 2π
Estudiaremos sólo aquellos puntos que estén dentro del período de la función:
(0, π/2) , (π/2, π) , (π, 3π/2) , (3π/2 , 2π)
| Intervalo | (0, π/2) | (π/2, π) | (π, 3π/2) | (3π/2 , 2π) |
|---|---|---|---|---|
| Punto de prueba | f ' ( π/4) > 0 | f ' (3π/4) < 0 | f ' (5π/4) < 0 | f ' (7 π/4) > 0 |
| Signo de f ' (x) | + | - | - | + |
| Monotonía | Crece | Decrece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 0 , x = π/2 , x = π , x = 3π/2 , x = 2π , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = - 3 sen x + 9 sen 3x
• f '' (0) = 0 ⇒ no es ni máximo ni mínimo
• f '' (π/2) < 0 ⇒ Hay un máximo en x = π/2 ⇒ f(π/2) = 4 ⇒ Max (π/2, 4)
• f '' (π) = 0 ⇒ no es ni máximo ni mínimo
• f '' (3π/2) > 0 ⇒ Hay un mínimo en x = 3π/2 ⇒ f(3π/2) = - 4 ⇒ Min (3π/2, -4)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
f '' (x) = - 3 sen x + 9 sen 3x = 0 ⇒ 9 sen 3x = 3 sen x ⇒ 3 sen 3x = sen x ⇒ sen x - 3 sen 3x = 0
Anteriormente obtuvimos la fórmula del seno del ángulo triple:
sen 3x = 3 sen x cos2x - sen3x
Sustituimos en nuestra ecuación y simplificamos:
sen x - 3 sen 3x = 0 ⇒ sen x - 3 [ 3 sen x cos2x - sen3x ] = 0
sen x - 9 sen x cos2x + 3 sen3x = 0 ⇒ sen x [ 1 - 9 cos2x + 3 sen2x ] = 0
sen x [ 1 - 9 cos2x + 3 ( 1 - cos2x ) ] = 0 ⇒ sen x [ 1 - 9 cos2x + 3 - 3 cos2x ] = 0
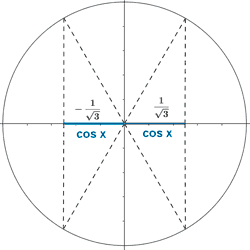
sen x [ 4 - 12 cos2x ] = 0 ⇒ 4 sen x [ 1 - 3 cos2x ] = 0
La ecuación será 0 cuando cualquiera de los factores sea 0:
sen x = 0 ⇒ x = 0 , x = π , x = 2π
![]()
Las soluciones del arcocoseno son: x = 0,95 x = 2,18 x = 4,10 x = 5,32
Puntos de inflexion para sen x = 0:
(0 , 0) , (π , 0) , (2π , 0)
Puntos de inflexión para 1 - 3cos2x = 0 :
(0,95 , 2,218) , (2,18 , 2,18) , (4,10 , -2,18) , (5,32 , -2,18)
Los puntos obtenidos anulan a la segunda derivada , y no anulan a la derivada tercera de la función, por tanto, son puntos de inflexión.
SELECTIVIDAD
Dada la siguiente función, calcular su dominio de definición, los puntos de corte con los ejes, sus intervalos de signo constante, sus máximos, mínimos y sus puntos de inflexión en el intervalo [0 , 2π] .
![]()
La función estará bien definida en todo R menos aquellos puntos que anulen al denominador:
2 - cos x = 0 ⇔ cos x = 2 , pero sabemos que - 1 < cos x < 1 ⇒ cos x ≠ 2 para todo x ∈ R
Como no existe ningún valor de x que anule al denominador, el dominio es todo R:
Dom(f) = R = (-∞, +∞)
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
![]()
Puntos de corte con el eje X:
![]()
Luego los puntos son: (0 , 0) , (π , 0) , (2π , 0)
Como los puntos de corte con el eje OX son x = 0 , x = π , x = 2π , y tenemos que estudiar la función en el intervalo [0 , 2π] , estudiaremos el signo en los intervalos: (0, π) , (π , 2π)
| Intervalo | (0, π) | (π , 2π) |
|---|---|---|
| Punto de prueba | f(π/2) > 0 | f(3π/2) < 0 |
| Signo de f (x) | + | - |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
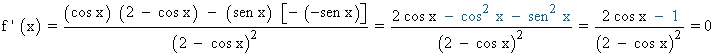
Para simplificar el resultado hemos aplicado la ecuación fundamental de la trigonometría:
sen2 x + cos2 x = 1 ⇒ - sen2 x - cos2 x = - 1
Resolvemos la ecuación para los x ∈ [0 , 2π] :
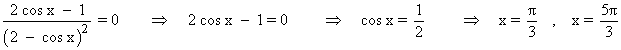
Tenemos que estudiar la monotonía en los intervalos: (0, π/3) , (π/3 , 5π/3) , (5π/3 , 2π)
| Intervalo | (0, π/3) | (π/3 , 5π/3) | (5π/3 , 2π) |
|---|---|---|---|
| Punto de prueba | f ' ( π/4) > 0 | f ' (π) < 0 | f ' (7π/4) > 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = π/3 y x = 5π/3 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda:
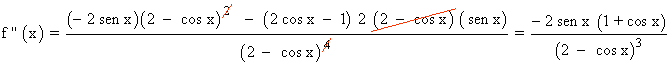
• f '' (π/3) < 0 ⇒ Hay un máximo en x = π/3 ⇒ f(π/3) = √3/3 ⇒ Max (π/3, √3/3)
• f '' (5π/3) > 0 ⇒ Hay un mínimo en x = 5π/3 ⇒ f(5π/3) = - √3/3 ⇒ Min (5π/3, - √3/3)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
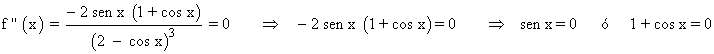
⇒ sen x = 0 ⇒ x = 0 , x = π , x = 2π
⇒ 1 + cos x = 0 cos x = - 1 ⇒ x = π
Tenemos que estudiar los siguientes intervalos: (0, π) , (π , 2π):
| Intervalo | (0, π) | (π , 2π) |
|---|---|---|
| Punto de prueba | f '' ( π/2) < 0 | f '' (3π/2) < 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Cóncava (∪) |
La función es cóncava hacia arriba o simplemente cóncava en (π , 2π) y cóncava hacia abajo o convexa en (0, π) .
Puntos de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = 0 , x = π , x = 2π y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
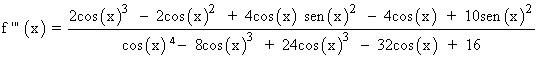
f ''' (0) ≠ 0 ⇒ x = 0 es la abscisa del punto de inflexión ⇒ f(0) = 0 ⇒ Punto inflexión (0 , 0)
f ''' (π) ≠ 0 ⇒ x = π es la abscisa del punto de inflexión ⇒ f(π) = 0 ⇒ Punto inflexión (π, 0)
f ''' (2π) ≠ 0 ⇒ x = 2π es la abscisa del punto de inflexión ⇒ f(2π) = 0 ⇒ Punto inflexión (2π, 0)
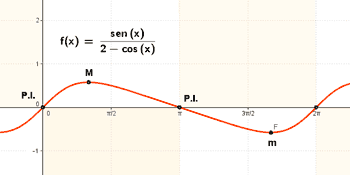
SELECTIVIDAD
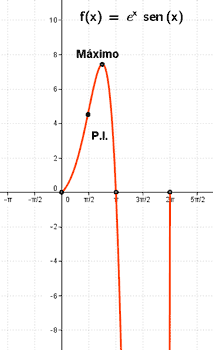
Calcular los extremos y los puntos de inflexión de la función dada por la ecuación f(x) = ex sen x en el intervalo [0 , 2π] .
Seguiremos los siguientes puntos:
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
f ' (x) = ex sen x + ex cos x = ex (sen x + cos x) = 0 ⇒ sen x + cos x = 0 (ex ≠ 0 para todo x∈R)
Resolvemos la ecuación para los x ∈ [0 , 2π] :
sen x + cos x = 0 ⇒ sen x = - cos x ⇒ x = 3π/4 , x = 7π/4
Tenemos que estudiar la monotonía en los intervalos: (0, 3π/4) , (3π/4 , 7π/4) , (7π/4 , 2π)
| Intervalo | (0, 3π/4) | (3π/4 , 7π/4) | (7π/4 , 2π) |
|---|---|---|---|
| Punto de prueba | f ' ( π/4) > 0 | f ' (π) < 0 | f ' (11π/6) > 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 3π/4 y x = 7π/4 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda:
f '' (x) = ex(sen x + cos x) + ex(cos x - sen x) = ex (sen x + cos x + cos x - sen x) = 2 ex cos x
• f '' (3π/4) < 0 ⇒ Hay un máximo en x =3π/4 ⇒ f3π/4) = e3π/4 √2/2 ⇒ Max (3π/4 , e3π/4 √2/2)
• f '' (7π/4) > 0 ⇒ Hay un mínimo en x = 7π/4 ⇒ f(7π/4) = - e3π/4 √2/2 ⇒ Min (7π/4 , - e3π/4 √2/2 )
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = 2 ex cos x = 0 ⇒ cos x = 0 , (ex≠0 para todo x ∈ R) ⇒ x = π/2 , x = 3π/2
Tenemos que estudiar los siguientes intervalos: (0, π/2) , ( π/2, 3π/2) , (3π/2, 2π)
| Intervalo | (0, π/2) | ( π/2, 3π/2) | (3π/2, 2π) |
|---|---|---|---|
| Punto de prueba | f '' ( π/4) > 0 | f '' (π) < 0 | f '' (7π/4) > 0 |
| Signo de f '' (x) | + | - | + |
| Curvatura | Cóncava (∪) | Convexa (∩) | Cóncava (∪) |
La función es cóncava hacia arriba o simplemente cóncava en (0, π/2)∪ (3π/2, 2π) y cóncava hacia abajo o convexa en ( π/2, 3π/2) .
Puntos de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = π/2 , x = 3π/2 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f ''' (x) = 2 ex cos x + 2 ex (- sen x) = 2 ex (cos x - sen x)
f ''' (π/2) ≠ 0 ⇒ x = π/2 es la abscisa del punto de inflexión ⇒ f(π/2) = eπ/2 ⇒ Punto inflexión (π/2, eπ/2)
f ''' (3π/2) ≠ 0 ⇒ x =3π/2 es la abscisa del punto de inflexión ⇒ f(3π/2) = - eπ/2 ⇒ Punto inflexión (3π/2 , - eπ/2)
Representa gráficamente la curva f(x) = x - arc tg x determinando el dominio de la función, simetrías, asíntotas, máximos, mínimos e intervalos de crecimiento y decrecimiento.
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) : R = (-∞, +∞)
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 0 - arc tg 0 = 0 ⇒ (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ x - arc tg x = 0 ⇒ x = arc tg x ⇒ x = 0 ⇒ (0 , 0)
f(-x) = - x - arc tg (-x) = - x - (- arc tg x) = - x + arc tg x = - f(x) ⇒ tiene simetría impar
Luego la función es simétrica respecto al eje OX.
Asíntotas
La función no tiene asíntotas verticales.
Observamos que:
![]()
![]()
![]()
![]()
Por tanto, la función tiene dos asíntotas oblicuas que son:
![]()
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
![]()
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (-∞, 0) , (0, +∞)
| Intervalo | (-∞, 0) | (0, +∞) |
|---|---|---|
| Punto de prueba | f ' ( - √3) > 0 | f ' (√3) > 0 |
| Signo de f ' (x) | + | + |
| Monotonía | Crece | Crece |
Por el apartado anterior sabemos que el punto crítitco o punto que anula a la derivada primera es x = 0 , vamos a determinar a través de la segunda derivada si se trata de máximo o mínimo.
Hallamos la derivada segunda:
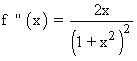
• f '' (0) = 0 ⇒ el punto x = 0 no es máximo ni mínimo
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
f '' (0) = 0 ⇒ x = 0 puede ser un punto de inflexión
Tenemos que estudiar los siguientes intervalos: (-∞, 0) , (0, +∞)
| Intervalo | (-∞, 0) | (0, +∞) |
|---|---|---|
| Punto de prueba | f '' ( -1) < 0 | f '' ( 1) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente cóncava en (0, +∞) y cóncava hacia abajo o convexa en (-∞, 0) .
Punto de inflexión
Por el apartado anterior sabemos que el punto que anula a la derivada segunda es x = 0 y vamos a determinar a través de la tercera derivada si se trata de un punto de inflexión.
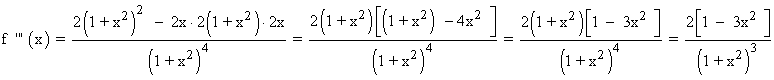
f ''' (0) = 2 ≠ 0 ⇒ x = 0 es la abscisa del punto de inflexión ⇒ f(0) = 0 ⇒ Punto inflexión (0, 0)
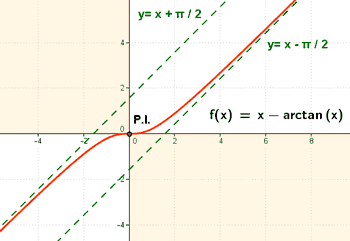
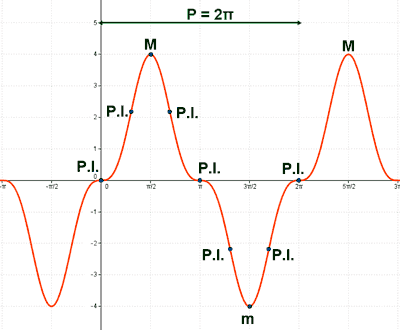
Representa gráficamente la función: y = sen2 x
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) : Calcularemos su imagen o recorrido a través de su función invesa
y = sen2(x) ⇒ ±√y = sen(x) ⇒ arcsen(±√y) = x
Intercambiamos las variables y estudiamos el dominio de la nueva función: y = arcsen(±√x)
• El dominio de la función arc sen(x) es: [-1 , 1]
• La raíz cuadrada está bien definida sólo en los números positivos: [0 , ∞)
Por tanto, su dominio es: [-1 , 1] ∩ [0 ,∞) = [0 , 1]
O lo que es lo mismo, la imagen de nuestra función es: Im(f) = [0 , 1]
Vamos a escribir f(x) de otra forma equivalente que nos permita calcular su período.
Usaremos la fórmula del coseno del ángulo doble: cos(2x) = cos2(x) - sen2(x)
Y también: 1 = cos2(x) + sen2(x)
cos(2x) = cos2(x) - sen2(x) ⇔ cos(2x) = (1 - sen2(x) ) - sen2(x) ⇔ cos(2x) = 1 - 2sen2(x) ⇔
⇔ 2sen2(x) = 1 - cos(2x) ⇔ sen2(x) = (1 - cos(2x) )/2
Ahora sí sabemos calcular su período teniendo en cuenta que el período de la función coseno es 2π :
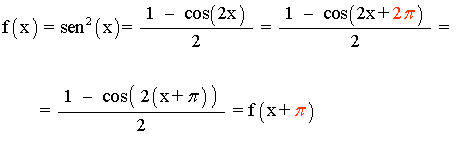
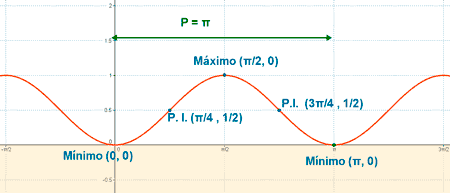
El período de f(x) es T = π .
Por tanto haremos el estudio de la función en el intervalo: [0 , π )
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función trigonométrica.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = sen2(0) ⇒ y = 0 ⇒ (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = sen2(x) ⇒ 0 = ± sen(x) ⇒ x = 0 ó x = π
Luego los puntos de corte con el eje X son: (0 , 0) , (π , 0)
Como los puntos de corte con el eje OX son x = 0 y x = π , y el período de la función es [0 , π ) , estudiaremos el signo en el intervalo: (0, π)
| Intervalo | (0, π) |
|---|---|
| Punto de prueba | f(π/2) > 0 |
| Signo de f (x) | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
f(- x) = sen2(-x) = (- sen(x))2 = sen2 x = f(x) ⇒ Tiene simetría par.
sen (-x) = - sen x
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = 2 sen (x) cos (x)= 0 ⇒ 2 sen (x) cos (x) = 0
La ecuación será igual a 0 cuando sen(x)= 0 ó cos(x) = 0
sen (x) = 0 ⇔ x = 0 , x = π
cos(x) = 0 ⇔ x = π/2
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (0, π/2) , (π/2, π)
| Intervalo | (0 , π/2) | (π/2 , π) |
|---|---|---|
| Punto de prueba | f ' ( π/3) > 0 | f ' (3π/4) < 0 |
| Signo de f ' (x) | + | - |
| Monotonía | Crece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 0 , x = π y x = π/2 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = 2( cos(x) cos(x) - sen(x) sen(x) ) = 2( cos2x - sen2x )
• f '' (0) = 2 > 0 ⇒ Hay un mínimo en x = 0 ⇒ f(0) = 0 ⇒ Min (0, 0)
• f '' (π) = 2 > 0 ⇒ Hay un mínimo en x = π ⇒ f(π) = 0 ⇒ Min (π, 0)
• f '' (π/2) = -2 < 0 ⇒ Hay un máximo en x = π/2 ⇒ f(π/2) = 1 ⇒ Min (π/2, 1)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = 2( cos2x - sen2x ) = 0 ⇒ cos2x = sen2x ⇒ cos x = sen x ⇒ x = π/4 , x = π/4 + π/2 = 3π/4
Por tanto, los puntos que anulan la ecuación son: x = π/4 , x = 3π/4
Tenemos que estudiar los siguientes intervalos: (0, π/4) , ( π/4, 3π/4) , (3π/4 , π):
| Intervalo | (0, π/4) | ( π/4, 3π/4) | (3π/4 , π) |
|---|---|---|---|
| Punto de prueba | f '' ( π/6) > 0 | f '' ( π/2) < 0 | f '' (2π/3) > 0 |
| Signo de f '' (x) | + | - | + |
| Curvatura | Concava (∪) | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente concava en (0, π/4) ∪ (3π/4 , π) y concava hacia abajo o convexa en el intervalo ( π/4, 3π/4) .
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = π/4 , x = 3π/4 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f ''' (x) = 2[ - 2cos(x)sen(x) - 2sen(x)cos(x) ] = 2[ - 4cos(x)sen(x) ] = - 8cos(x)sen(x)
f ''' (π/4) = - 4 ≠ 0 ⇒ x = π/4 es la abscisa del punto de inflexión ⇒ f(π/4) = 1/2 ⇒ Punto inflexión ( π/4, 1/2)
f ''' (3π/4) = 4 ≠ 0 ⇒ x = 3π/4 es la abscisa del punto de inflexión ⇒ f(3π/4) = 1/2 ⇒ Punto inflexión (3π/4, 1/2)
SELECTIVIDAD
Representa gráficamente la función:
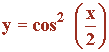
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) = [0 , 1]
Sabemos que: - 1 ≤ cos (x/2) ≤ 1
Elevando al cuadrado: 0 ≤ cos2(x/2) ≤ 1
Vamos a calcular primero la periodicidad de la función: f(x) = cos2(x)
f(x) = cos2 x = (cos x )2 = (- cos x)2
Podemos relacionar el coseno del primer cuadrante con el del segundo cuadrante así:
- cos x = cos (x + π)
f(x) = cos2 x = (- cos x)2 = (cos (x + π) )2 = cos2 (x + π) = f(x + π)
Veamos ahora el periodo de la función que nos piden teniendo en cuenta que el periodo de cos2(x) es π :
![]()
Por tanto haremos el estudio de la función en el intervalo: [0 , 2π )
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función trigonométrica.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = cos2 0 = 1
Luego los puntos de corte con el eje Y son: (0 , 1)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = cos2(x/2) ⇒ 0 = cos(x/2) ⇒ x/2 = π/2 + kπ k∈Z ⇒ x = π + 2kπ k∈Z
Los puntos que pertenecen al primer periodo de la función [0 , 2π):
Sabemos que la función coseno tiene simetría par: cos (-x) = cos (x)
Entonces:
f(- x) = cos2(- x/2) = cos2(x/2) = f(x) ⇒ Tiene simetría par.
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
Para simplificar la derivada hemos usado la fórmula del ángulo doble: 2 sen x cos x = sen 2x![]()
Igualamos la primera derivada a 0:
![]()
Los puntos del primer periodo de la función [0 , 2π) que anulan a la primera derivada son:
• k = 0 : x = 0·π = 0
• k = 1 : x = 1·π = π
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (0 , π) , (π , 2π)
| Intervalo | (0 , π) | (π , 2π) |
|---|---|---|
| Punto de prueba | f ' ( π/2) < 0 | f ' (3π/2) > 0 |
| Signo de f ' (x) | - | + |
| Monotonía | Decrece | C rece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 0 y x = π , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = - 1/2 cos x
• f '' (0) = - 1/2 < 0 ⇒ Hay un máximo en x = 0 ⇒ f(0) = 1 ⇒ Max (0, 1)
• f '' (π) = 1/2 > 0 ⇒ Hay un mínimo en x =π ⇒ f(π) = 0 ⇒ Min (π, 0)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = - 1/2 cos x = 0 ⇒ cos x = 0 ⇒ x = π/2 + kπ k∈Z
Veamos qué puntos están dentro del primer periodo de la función [0 , 2π) :
• k = 0 : x = π/2 + 0 = π/2
• k = 1 : x = π/2 + π = 3π/2
Por tanto, los puntos que anulan la segunda derivada son: x = π/2 , x =3π/2
Tenemos que estudiar los siguientes intervalos: (0, π/2) , ( π/2, 3π/2) , (3π/2 , 2π)
| Intervalo | (0, π/2) | ( π/2, 3π/2) | (3π/2 , 2π) |
|---|---|---|---|
| Punto de prueba | f '' ( π/4) < 0 | f '' ( π) > 0 | f '' (7π/4) < 0 |
| Signo de f '' (x) | - | + | - |
| Curvatura | Convexa (∩) | Concava (∪) | Convexa (∩) |
La función es cóncava hacia arriba o simplemente concava en ( π/2, 3π/2) y concava hacia abajo o convexa en el intervalo (0, π/2) ∪ (3π/2 , 2π) .
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = π/2 , x = 3π/2 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f ''' (x) = - 1/2 ( - sen x ) = 1/2 sen x
f ''' (π/2) = 1/2 ≠ 0 ⇒ x = π/2 es la abscisa del punto de inflexión ⇒ f(π/2) = 1/2 ⇒ Punto inflexión ( π/2, 1/2)
f ''' (3π/2) = -1/2 ≠ 0 ⇒ x = 3π/2 es la abscisa del punto de inflexión ⇒ f(3π/2) = 1/2 ⇒ Punto inflexión (3π/2, 1/2)
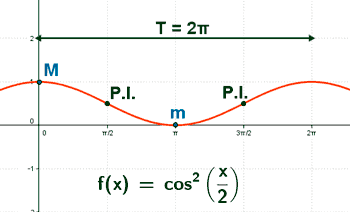
SELECTIVIDAD
a) Obtener los intervalos de crecimiento y decrecimiento de la función y = cos2x + cos x en el intervalo [0 , 2π] .
b) Encontrar los extremos relativos y absolutos de dicha función.
a) Obtener los intervalos de crecimiento y decrecimiento de la función y = cos2x + cos x en el intervalo [0 , 2π] .
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
f ' (x) = 2 cos x (- sen x) + (- sen x) = - 2 cos x sen x - sen x = - sen x (2 cos x + 1) = 0
Resolvemos la ecuación para los x ∈ [0 , 2π] :
⇒ sen x = 0 ⇒ x = 0 , x = π , x = 2π
⇒ 2 cos x + 1 = 0 ⇒ cos x = - 1/2 ⇒ x = 2π/3 , x = 4π/3
Tenemos que estudiar la monotonía en los intervalos: (0, 2π/3) , (2π/3 , π) , (π , 4π/3) , (4π/3 , 2π)
| Intervalo | (0, 2π/3) | (2π/3 , π) | (π , 4π/3) | (4π/3 , 2π) |
|---|---|---|---|---|
| Punto de prueba | f ' ( π/2) < 0 | f ' (3π/4) > 0 | f ' (5π/4) < 0 | f ' (3π/2) > 0 |
| Signo de f ' (x) | - | + | - | + |
| Monotonía | Decrece | Crece | Decrece | Crece |
b) Encontrar los extremos relativos y absolutos de dicha función.
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 0 , x = 2π/3 , x = π , x = 4π/3 y x = 2π , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda:
f '' (x) = (- cos x) (2 cos x + 1) + (- sen x)(- 2 sen x) = - 4 cos2x - cos x + 2
• f '' (0) < 0 ⇒ Hay un máximo en x = 0 ⇒ f(0) = 2 ⇒ Max (0 , 2)
• f '' (2π/3) > 0 ⇒ Hay un mínimo en x = 2π/3 ⇒ f(2π/3) = -1/4 ⇒ Min (2π/3 , -1/4 )
• f '' (π) < 0 ⇒ Hay un máximo en x =π ⇒ f(π) =0 ⇒ Max (π , 0)
• f '' (4π/3) > 0 ⇒ Hay un mínimo en x = 4π/3 ⇒ f(4π/3) = -1/4 ⇒ Min (4π/3 , -1/4 )


 INICIO
INICIO