Ejercicios de representación de funciones a trozos
SELECTIVIDAD
Sea la función:
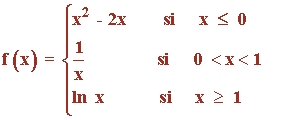
a) Representar gráficamente f(x)
b) A partir de su gráfica, estudiar el crecimiento de f(x)
c) Hallar los puntos de corte con los ejes
• Estudio en el intervalo (-∞, 0) :
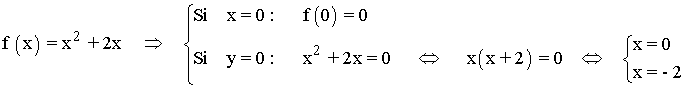
![]()
Para ver si en x = -1 hay un máximo o un mínimo relativo, vemos el signo de la primera derivada:
![]()
![]()
• Estudio en el intervalo (0, 1) :
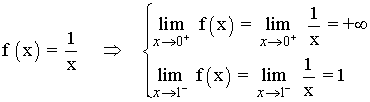
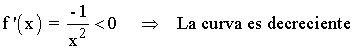
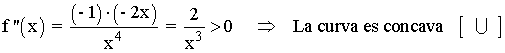
• Estudio en el intervalo (1, +∞) :
![]()
![]()
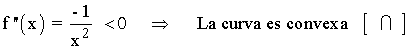
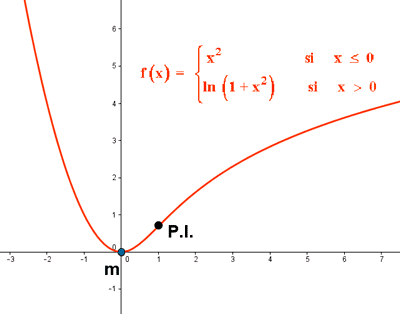
a) Una vez estudiados los distintos trozos de la función, podemos dibujar la gráfica:
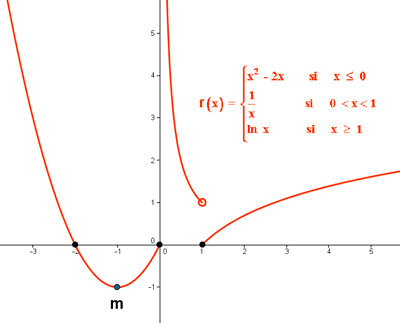
De la gráfica se puede deducir:
b) f(x) es creciente en (-1, 0) ∪ (1, +∞) y decreciente en (-∞, -1) ∪ (0, 1)
c) Los puntos de corte con los ejes son: (-2, 0) , (0, 0) , (1, 0)
SELECTIVIDAD
Sea la función:
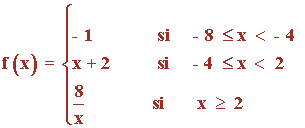
a) Representar gráficamente f(x)
b) Estudiar la continuidad y el crecimiento de f(x)
c) Determinar f-1(1)
d) Obtener la gráfica de | f(x) |
a) Representar gráficamente f(x)
• En el intervalo [-8, -4) la gráfica corresponde con la recta y = -1 .
• En el intervalo [-4, 2) la función es la recta y = x + 2 .
y ' = 1 > 0 ⇒ la gráfica es creciente en dicho intervalo.
• Estudiemos el comportamiento de la función en el intervalo [2, +∞) :
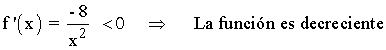
![]()
De esta forma podemos representar la gráfica de la función f(x) :
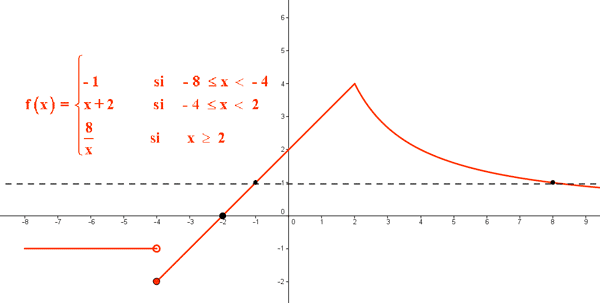
b) Estudiar la continuidad y el crecimiento de f(x)
La función es continua en cada trozo, por lo que vamos a estudiar la continuidad en los puntos de unión: x = -4 y x = 2
• x = -4
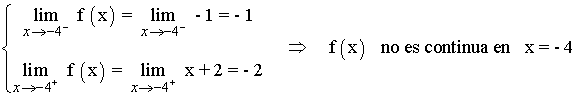
• x = 2
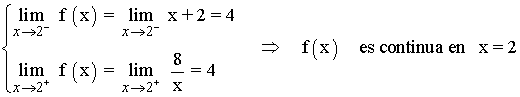
Por lo tanto, f(x) es continua en todo su dominio menos en x = -4
Además, observando la gráfica se deduce que la función es constante en el intervalo [-8, -4) , creciente en el intervalo ([-4, 2) y decreciente en el intervalo [2, +∞)
c) Determinar f-1(1)
Si en la gráfica trazamos la recta y = 1 observamos que corta a la función en dos intervalos:
• [-4, 2) : x + 2 = 1 ⇒ x = - 1
• [2, +∞) : 8/x = 1 ⇒ x = 8
Por lo tanto, tenemos que: f-1(1) = {-1, 8}
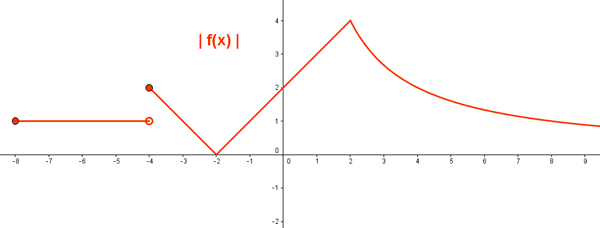
d) Obtener la gráfica de | f(x) |

Estudiamos por separado cada una de las ramas de la función f(x) :
![]()
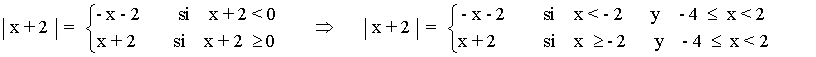
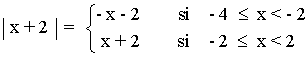
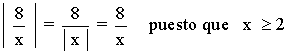
Por lo tanto la función | f(x) | queda definida de la siguiente manera:
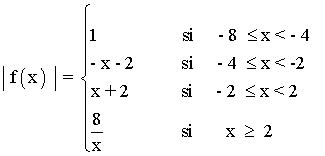
SELECTIVIDAD
Sea la función:
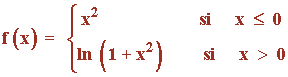
Estudiar la derivabilidad de f(x) , sus intervalos de crecimiento y decrecimiento, sus puntos de inflexión y representar gráficamente.
• Dom(f) = R = (-∞, +∞)
• Im(f) = R = [0, +∞)
La función f(x) es continua y derivable para x > 0 al tratarse de composición de funciones continuas y derivables) y también es continua y derivable para x < 0 al ser una función polinómica.
Por lo tanto tenemos que estudiar la continuidad y derivabilidad en x = 0 :
![]()
![]()
Por lo tanto los límites laterales coinciden y además ocurre que f(0) = 0 , por lo tanto f(x) es continua en x = 0 .
Además, tenemos que:
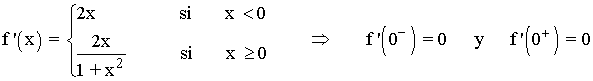
Es decir, la función f(x) es derivable en x = 0 .
• Corte con el eje OX: f(x) = 0
x2 = 0 ⇔ x = 0
ln (1 + x2) = 0 ⇔ 1 + x2 = e0 ⇔ 1 + x2 = 1 ⇔ x2 = 0 ⇔ x = 0
El punto de corte es: (0, 0)
• Corte con el eje OY: f(0)
f(0) = 02 = 0
El punto de corte es: (0, 0)
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
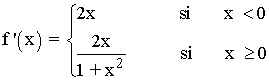
f ' (x) = 0 ⇔ 2x = 0 ⇔ x = 0
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, 0) , (0, +∞)
| Intervalo | (- ∞, 0) | (0, +∞) |
|---|---|---|
| Punto de prueba | f ' (-1) < 0 | f ' (1) > 0 |
| Signo de f ' (x) | - | + |
| Monotonía | Decrece | Crece |
Por el apartado anterior hemos obtenido un único punto que anula a la derivada primera (también llamado punto crítico) x = 0 , vamos a determinar a través de la segunda derivada si se trata de un máximo o de un mínimo.
Hallamos la derivada segunda:
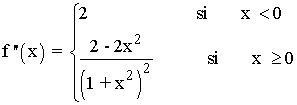
• f '' (0) = 2 > 0 ⇒ Hay un mínimo en x = 0 ⇒ f(0) = 0 ⇒ Min (0, 0)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
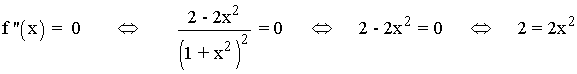
![]()
Como f ''(x) = 2 cuando x < 0 descartamos el valor x = -1 ya que no anula a la segunda derivada.
Por lo tanto tenemos que estudiar la curvatura en los siguientes intervalos: (-∞, 0) , (0, 1) , (1, +∞)
| Intervalo | (-∞, 0) | (0, 1) | (1, +∞) |
|---|---|---|---|
| Punto de prueba | f '' (-1) | f '' (0,5) | f '' (2) |
| Signo de f '' (x) | + | + | - |
| Curvatura | Concava (∪) | Concava (∪) | Convexa (∩) |
Punto de inflexión
Por el apartado anterior sabemos que el punto que anula a la derivada segunda es x = 1.
En este punto la función pasa de concava a convexa, por lo tanto se trata de un punto de inflexión.
f(1) = ln 2 ⇒ (1, ln 2) es un punto de inflexión


 INICIO
INICIO