INICIOFunciones simétricas
Funciones pares
Una función f es simétrica respecto al eje de ordenadas (Y) si verifica que:
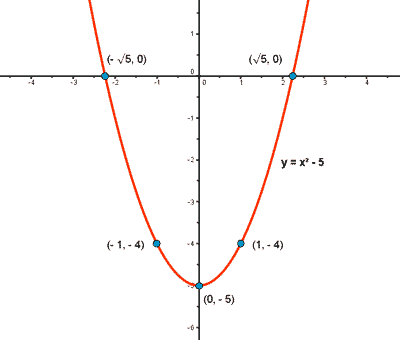
Las funciones simétricas respecto al eje de ordenadas se denominan funciones pares.
f(- x) = (- x)2 - 5 = x2 - 5
f(- x) = f(x)
Por lo tanto se cumple la condición de función par.
Funciones impares
Una función f es simétrica respecto al origen de coordenadas si verifica que:
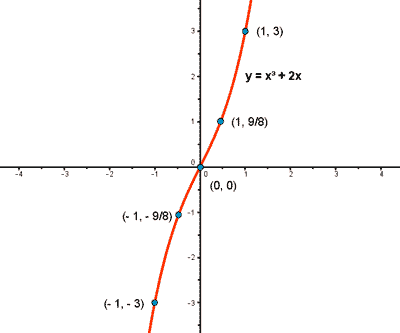
Las funciones simétricas respecto al origen de coordenadas se denominan funciones impares.
f(- x) = (- x)3 + 2·(- x) = - x3 - 2x = - (x3 + 2x)
f(- x) = - f(x)
Por lo tanto se cumple la condición de función impar.
Función que no es par ni impar
La función f(x) = x2 - 3x no es ni par ni impar, puesto que:
f(- x) = (- x)2 - 3·(- x) = x2 + 3x , por lo tanto f(- x) ≠ ± f(x)
