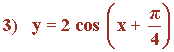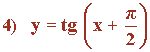Ejercicios de representación de funciones trigonométricas I
Representa las siguientes funciones trigonométricas:
1) y = 2 cos x
2) y = 3 sen (2x)
5) y = 1 - tg(2x)
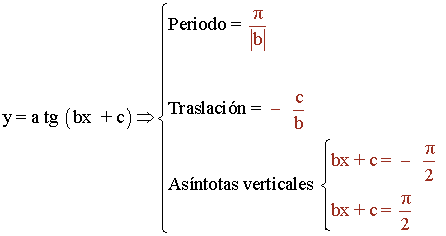
Funciones trigonométricas: periodo, amplitud, asíntotas verticales, dominio e imagen.
| Periodo | Amplitud | Asintotas verticales |
Dominio | Imagen | |
|---|---|---|---|---|---|
| y = sen x | 2π | 1 | No tiene | R | { y∈R | -1 ≤ y ≤ 1 } |
| y = cos x | 2π | 1 | No tiene | R | { y∈R | -1 ≤ y ≤ 1 } |
| y = tg x | π | π/2 (2k + 1) , k∈Z | { x∈R | x ≠ π/2 (2k + 1) } | R | |
| y = cotg x | π | k·π , k∈Z | { x∈R | x ≠k·π } | R | |
| y = sec x | 2π | π/2 (2k + 1) , k∈Z | { x∈R | x ≠ π/2 (2k + 1) } | { y∈R | y ≤ -1 ó y ≥ 1 } | |
| y = cosec x | 2π | k π , k∈Z | { x∈R | x ≠k·π } | { y∈R | y ≤ -1 ó y ≥ 1 } |
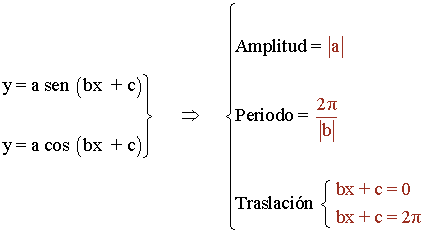
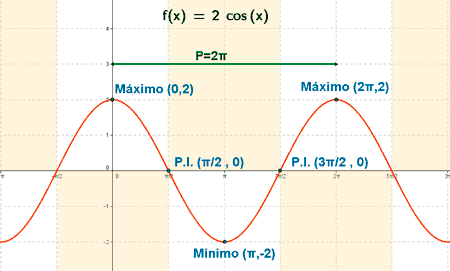
Representa gráficamente la función: y = 2 cos x
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) : [-2 , 2]
Como la función coseno es periódica de período 2π , la función f(x) = 2 cos(x) tiene el mismo período: 2π .
También podemos sacar el período de la función así:
f(x) = 2 cos(x) = 2 cos(x + 2π) = f(x + 2π)
Por tanto haremos el estudio de la función en el intervalo: [0 , 2π )
Periodo, amplitud y traslación:
Podemos calcular el periodo, la amplitud y la traslación de nuestra función como se indica en la primera sección (Resumen):
Amplitud = |2| = 2
Periodo = 2π/1 = 2π
Traslación : x = 0
x = 2π (igual al periodo)
No tiene traslación.
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función trigonométrica.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 2 cos 0 ⇒ y = 2 ⇒ (0 , 2)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 2 cos(x) ⇒ cos(x) = 0 ⇒ x = π/2 ó x = 3π/2
Luego los puntos de corte con el eje X son: (π/2 , 0) , (3π/2 , 0)
Como los puntos de corte con el eje OX son x = π/2 y x =3π/2 , y el período de la función es [0 , 2π ) , estudiaremos el signo en los intervalos: (0, π/2) , (π/2 , 3π/2) , (3π/2 , 2π)
| Intervalo | (0, π/2) | (π/2 , 3π/2) | (3π/2 , 2π) |
|---|---|---|---|
| Punto de prueba | f(π/4) > 0 | f(π) < 0 | f(7π/4) > 0 |
| Signo de f (x) | + | - | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
f(- x) = 2cos(-x) = 2cos(x) = f(x) ⇒ Tiene simetría par.
cos (-x) = cos (x)
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
f ' (x) = 2(-sen x) = - 2 sen (x)= 0 ⇒ sen (x) = 0 ⇒ x = 0 , x = π , x = 2π
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (0, π) , (π, 2π)
| Intervalo | (0 , π) | (π , 2π) |
|---|---|---|
| Punto de prueba | f ' ( π/2) < 0 | f ' (3π/2) > 0 |
| Signo de f ' (x) | - | + |
| Monotonía | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 0 , x = π y x = 2π , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = - 2 cos(x)
• f '' (0) = - 2 < 0 ⇒ Hay un máximo en x = 0 ⇒ f(0) = 2 ⇒ Max (0, 2)
• f '' (π) = 2 > 0 ⇒ Hay un mínimo en x = π ⇒ f(π) = - 2 ⇒ Min (π, - 2)
• f '' (2π) = -2 < 0 ⇒ Hay un máximo en x = 2π ⇒ f(2π) = 2 ⇒ Max (2π, 2)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = - 2 cos(x) = 0 ⇒ cos (x) = 0 ⇒ x = π/2 , x = 3π/2
Tenemos que estudiar los siguientes intervalos: (0, π/2) , ( π/2, 3π/2) , (3π/2 , 2π):
| Intervalo | (0, π/2) | ( π/2, 3π/2) | (3π/2 , 2π) |
|---|---|---|---|
| Punto de prueba | f '' ( π/4) < 0 | f '' ( π) > 0 | f '' (7π/4) < 0 |
| Signo de f '' (x) | - | + | - |
| Curvatura | Convexa (∩) | Concava (∪) | Convexa (∩) |
La función es cóncava hacia arriba o simplemente concava en ( π/2, 3π/2) y concava hacia abajo o convexa en (0, π/2) ∪ (3π/2 , 2π) .
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = π/2 , x = 3π/2 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f ''' (x) = - 2 (- sen(x) ) = 2 sen x
f ''' (π/2) = 2 ≠ 0 ⇒ x = π/2 es la abscisa del punto de inflexión ⇒ f(π/2) = 0 ⇒ Punto inflexión ( π/2, 0)
f ''' (3π/2) = - 2 ≠ 0 ⇒ x = 3π/2 es la abscisa del punto de inflexión ⇒ f(3π/2) = 0 ⇒ Punto inflexión (3π/2, 0)
SELECTIVIDAD
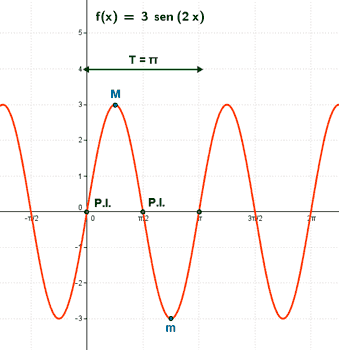
Representa gráficamente la función: y = 3 sen (2x)
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) = [-3 , 3]
Pues sabemos que: -1 < sen (2x)< 1
Y multiplicando por 3: -3 < 3 sen (2x) < 3
Sabemos que la función seno es periódica de periodo T = 2π , es decir: sen x = sen (x + 2π)
Por tanto:
f(x) = 3 sen (2x) = 3 sen (2x + 2π) = 3 sen 2(x + π) = f(x + π)
Luego nuestra función tiene periodo T = π .
Por tanto haremos el estudio de la función en el intervalo: [0 , π )
Periodo, amplitud y traslación:
Podemos calcular el periodo, la amplitud y la traslación de nuestra función como se indica en la primera sección (Resumen):
Amplitud = |3| = 3
Periodo = 2π/2 = π
Traslación : 2x = 0
2x = 2π ⇒ x = π (igual al periodo)
No tiene traslación.
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función trigonométrica.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 3 sen 0 = 0
Luego el punto de corte con el eje Y es: (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 3 sen (2x) ⇒ sen (2x) = 0 ⇒ 2x = kπ k∈Z ⇒ x = kπ/2 k∈Z
Los puntos que están dentro del periodo [0 , π) son:
• k = 0 : x = 0
• k = 1 : x = π/2
Luego los puntos de corte con el eje X son: (0 , 0) , (π/2, 0)
Sabemos que la función seno tiene simetría impar: sen (-x) = - sen(x)
Por tanto:
f(- x) = 3 sen (-2x) = - 3 sen (2x) = - f(x) ⇒ Tiene simetría impar.
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = 3 cos (2x)
f ' (x) = 3 cos (2x) = 0 ⇒ cos (2x) = 0 ⇒ 2x = π/2 + kπ k∈Z ⇒ x = π/4 + k π/2 k∈Z
Los puntos del primer periodo de la función [0 , π) que anulan a la primera derivada son:
• k = 0 : x = π/4 + 0 = π/4
• k = 1 : x = π/4 + π/2 = 3π/4
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (0 , π/4) , (π/4 , 3π/4) , (3π/4 , π)
| Intervalo | (0 , π/4) | (π/4 , 3π/4) | (3π/4 , π) |
|---|---|---|---|
| Punto de prueba | f ' ( π/6) > 0 | f ' (π/2) < 0 | f ' (5π/6) > 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = π/4 y x =3π/4 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = - 3 sen (2x) · 2 = - 6 sen (2x)
• f '' (π/4) = - 6 < 0 ⇒ Hay un máximo en x = π/4 ⇒ f(π/4) = 3 ⇒ Max (π/4, 3)
• f '' (3π/4) = 6 > 0 ⇒ Hay un mínimo en x =3π/4 ⇒ f(3π/4) = - 3 ⇒ Min (3π/4, - 3)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = - 6 sen (2x) = 0 ⇒ sen (2x) = 0 ⇒ 2x =kπ k∈Z ⇒ x = kπ/2 k∈Z
Veamos qué puntos están dentro del primer periodo de la función [0 , π) :
• k = 0 : x = 0
• k = 1 : x = π/2
Por tanto, los puntos que anulan la segunda derivada son: x = 0 , x =π/2
Tenemos que estudiar los siguientes intervalos: (0, π/2) , ( π/2, π)
| Intervalo | (0, π/2) | ( π/2, π) |
|---|---|---|
| Punto de prueba | f '' ( π/4) < 0 | f '' ( 3π/4) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente concava en ( π/2, π) y concava hacia abajo o convexa en el intervalo (0, π/2) .
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = 0 , x = π/2 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f ''' (x) = - 6 cos (2x) · 2 = - 12 cos (2x)
f ''' (0) = - 12 ≠ 0 ⇒ x = 0 es la abscisa del punto de inflexión ⇒ f(0) = 0 ⇒ Punto inflexión (0 , 0)
f ''' (π/2) = 12 ≠ 0 ⇒ x = π/2 es la abscisa del punto de inflexión ⇒ f(π/2) = 0 ⇒ Punto inflexión (π/2, 0)
SELECTIVIDAD
Representa gráficamente la función:
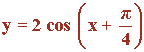
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) = [-2 , 2]
Pues sabemos que: -1 < cos (x + π/4) < 1
Y multiplicando por 2: -2 < 2 cos (x + π/4) < 2
Sabemos que la función coseno es periódica de periodo T = 2π .
Por tanto haremos el estudio de la función en el intervalo: [0 , 2π )
Periodo, amplitud y traslación:
Podemos calcular el periodo, la amplitud y la traslación de nuestra función como se indica en la primera sección (Resumen):
Amplitud = |2| = 2
Periodo = 2π/1 = 2π
Traslación : x + π/4 = 0 ⇒ x = - π/4
x + π/4 = 2π ⇒ x = 7π/4
Tiene una traslación hacia la izquierda paralela al eje OX con una distancia de π/4 .
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función trigonométrica.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 2 cos (π/4) = √2
Luego los puntos de corte con el eje Y son: (0 , √2)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 2 cos (x + π/4) ⇒ x + π/4 = π/2 , x + π/4 = 3π/2 ⇒ x = π/4 , x = 5π/4
Luego los puntos de corte con el eje X son: ( π/4 , 0) , (5π/4, 0)
Sabemos que la función coseno tiene simetría par: cos (-x) = cos (x)
Como nuestra función está desplazada π/4 , presenta el mismo tipo de simetría:
f(- x) = 2 cos (-x + π/4) = 2 cos (x + π/4) = f(x) ⇒ Tiene simetría par.
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = - 2 sen (x + π/4)
f ' (x) = - 2 sen (x + π/4) = 0 ⇒ sen (x + π/4) = 0 ⇒ x + π/4 = kπ k∈Z ⇒ x = - π/4 + kπ k∈Z
Los puntos del primer periodo de la función [0 , 2π) que anulan a la primera derivada son:
• k = 1 : x = - π/4 + π = 3π/4
• k = 2 : x = - π/4 + 2π = 7π/4
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (0 , 3π/4) , (3π/4 , 7π/4) , (7π/4 , 2π)
| Intervalo | (0 , 3π/4) | (3π/4 , 7π/4) | (7π/4 , 2π) |
|---|---|---|---|
| Punto de prueba | f ' ( π/2) < 0 | f ' (π) > 0 | f ' (11π/6) < 0 |
| Signo de f ' (x) | - | + | - |
| Monotonía | Decrece | C rece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 3π/4 y x =7π/4 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = - 2 cos (x + π/4)
• f '' (3π/4) = 2 > 0 ⇒ Hay un mínimo en x = 3π/4 ⇒ f(3π/4) = -2 ⇒ Min (3π/4, -2)
• f '' (7π/4) = -2 < 0 ⇒ Hay un máximo en x =7π/4 ⇒ f(7π/4) = 2 ⇒ Max (7π/4, 2)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = - 2 cos (x + π/4) = 0 ⇒ cos (x + π/4) = 0 ⇒ x = π/4 + kπ k∈Z
Veamos qué puntos están dentro del primer periodo de la función [0 , 2π) :
• k = 0 : x = π/4
• k = 1 : x = π/4 + π = 5π/4
Por tanto, los puntos que anulan la segunda derivada son: x = π/4 , x =5π/4
Tenemos que estudiar los siguientes intervalos: (0, π/4) , ( π/4, 5π/4) , (5π/4 , 2π)
| Intervalo | (0, π/4) | ( π/4, 5π/4) | (5π/4 , 2π) |
|---|---|---|---|
| Punto de prueba | f '' ( π/6) < 0 | f '' ( π) > 0 | f '' (3π/2) < 0 |
| Signo de f '' (x) | - | + | - |
| Curvatura | Convexa (∩) | Concava (∪) | Convexa (∩) |
La función es cóncava hacia arriba o simplemente concava en ( π/4, 5π/4) y concava hacia abajo o convexa en el intervalo (0, π/4) ∪ (5π/4 , 2π) .
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = π/4 , x = 5π/4 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f ''' (x) = - 2 [ - sen (x + π/4) ] = 2 sen (x + π/4)
f ''' (π/4) = 2 ≠ 0 ⇒ x = π/4 es la abscisa del punto de inflexión ⇒ f(π/4) = 0 ⇒ Punto inflexión ( π/4, 0)
f ''' (5π/4) = -2 ≠ 0 ⇒ x = 5π/4 es la abscisa del punto de inflexión ⇒ f(5π/4) = 0 ⇒ Punto inflexión (5π/4, 0)
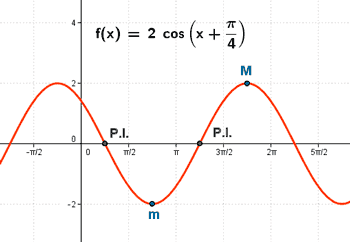
Representa gráficamente la función:
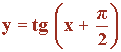
Función trigonométrica.
• Dom(f) = R - { kπ , k ∈ N }
• Im(f) : R
Sabemos que la función tangente es periódica de periodo π , entonces:
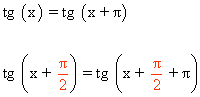
Nuestra función es periódica de periodo π .
Por tanto, haremos el estudio de la función en el intervalo: [0 , π)
Periodo, asíntotas verticales y traslación:
Podemos calcular el periodo, la amplitud y la traslación de nuestra función como se indica en la primera sección (Resumen):
Periodo = π/1 = π
Asíntotas verticales: x + π/2= - π/2 ⇒ x = - π
x + π/2 = π/2 ⇒ x = 0
Traslación : - (π/2)/1 = - π/2
Tiene una traslación hacia la izquierda paralela al eje OX con una distancia de - π/2 .
Continuidad y tipos de discontinuidad
La función es continua en todo su dominio.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 la función y = tg (π/2) no está definida, luego no corta al eje Y.
Puntos de corte con el eje X:
![]()
Para k = 1 tenemos que x = π/2 , luego el punto de corte con el eje X en el primer periodo de la función es: (π/2 , 0)
Como el punto de corte con el eje OX es x = π/2 , y el período de la función es [0 , π ) , estudiaremos el signo en los intervalos: (0, π/2) , (π/2 , π)
| Intervalo | (0, π/2) | (π/2 , π) |
|---|---|---|
| Punto de prueba | f(π/4) < 0 | f(3π/4) > 0 |
| Signo de f (x) | - | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
![]()
Por tanto, la función tiene simetría impar.
Asíntotas
Calculamos los límites laterales en el intervalo [0 , π) :
![]()
Luego las rectas x = 0 y x = π son asíntotas verticales.
Como es una función periódica, no tiene sentido estudiar los límites en el infinito. Por tanto, no tiene asíntotas horizontales ni tampoco oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
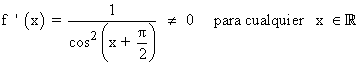
Si la derivada primera no se anula en ningún punto, la función no tiene máximos ni mínimos, y por tanto, la función es creciente en todo el intervalo [0 , π), o bien es decreciente.
Estudiaremos la monontonía en todo el intervalo [0 , π) :
| Intervalo | (0 , π) |
|---|---|
| Punto de prueba | f ' ( π/2) > 0 |
| Signo de f ' (x) | + |
| Monotonía | Crece |
Anteriormente hemos visto que la función no tiene máximos ni mínimos, ya que su primera derivada no se anula.
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
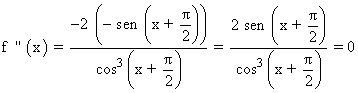
Observamos que será igual a 0 si el numerador es 0 :
![]()
Como estamos en el periodo [0 , π) sólo nos quedamos con el punto de inflexión x = π/2 .
Tenemos que estudiar los siguientes intervalos: (0, π/2) , ( π/2, π)
| Intervalo | (0, π/2) | ( π/2, π) |
|---|---|---|
| Punto de prueba | f '' ( π/4) < 0 | f '' ( 3π/4) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente cóncava en ( π/2, π) y cóncava hacia abajo o convexa en (0, π/2) .
Punto de inflexión
Por el apartado anterior sabemos que el punto que anula a la derivada segunda (dentro de nuestro periodo) es x = π/2 y vamos a determinar a través de la tercera derivada si se trata de un punto de inflexión.
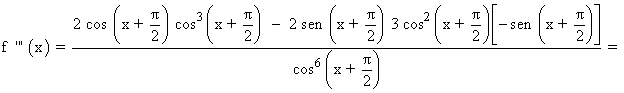
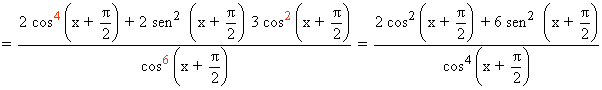
f ''' (π/2) ≠ 0 ⇒ x = π/2 es la abscisa del punto de inflexión ⇒ f(π/2) = 0 ⇒ Punto inflexión ( π/2, 0)
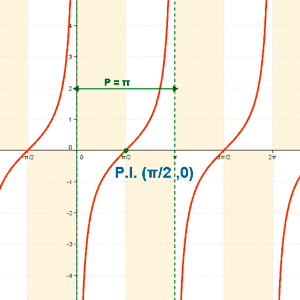
Representa gráficamente la función:
y = 1 - tg(2x)
Función trigonométrica.
• Dom(f) :
Sabemos que la función tg x no está definida si x = π/2
En nuestro caso, la función no estará definida si:
2x = π/2 ⇒ x = π/4
Dom(f) = R - { kπ/4 , k ∈ N }
• Im(f) : R
Sabemos que la función tangente es periódica de periodo π , entonces:
0 ≤ 2x ≤π ⇒ 0 ≤ x ≤ π/2
Nuestra función es periódica de periodo π/2 .
Por tanto, haremos el estudio de la función en el intervalo: [0 ,π/2)
Podemos calcular el periodo de nuestra función como se indica en la primera sección (Resumen):
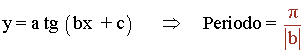
Periodo = π/2
Continuidad y tipos de discontinuidad
La función es continua en todo su dominio.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ f(0) = 1 - tg 0 = 1 ⇒ (0 , 1)
Puntos de corte con el eje X:
Si y = 0 ⇒ 1 - tg (2x) = 0 ⇒ tg(2x) = 1 ⇒ 2x = π/4 ⇒ x = π/8 ⇒ (π/8 , 0)
La función tg x tiene simetría impar: tg (-x) = - tg x
f(-x) = 1 - tg(-2x) = 1 - ( - tg 2x ) = 1 + tg(2x) ≠ f(x)
f(-x) = 1 - tg(-2x) = 1 - ( - tg 2x ) = 1 + tg(2x) ≠ - f(x)
No tiene ni simetría par ni impar.
Asíntotas
El único punto dentro del primer periodo, [0 , π/2) , en el que la función no está definida es el π/4.
Calculamos los límites laterales en dicho punto:

Luego la recta x = π/4 es asíntota vertical.
Como es una función periódica, no tiene sentido estudiar los límites en el infinito. Por tanto, no tiene asíntotas horizontales ni tampoco oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obtenidos:
![]()
Si la derivada primera no se anula en ningún punto, la función no tiene máximos ni mínimos, y por tanto, la función es creciente en todo el intervalo [0 , π), o bien es decreciente.
Estudiaremos la monontonía en el primer periodo de la función [0 , π/2) excepto en aquellos puntos en los que la función no está definida: [0 , π/4) , (π/4 , π/2)
| Intervalo | (0 ,π/4) | (π/4 , π/2) |
|---|---|---|
| Punto de prueba | f ' ( π/6) < 0 | f ' ( π/3) < 0 |
| Signo de f ' (x) | - | - |
| Monotonía | Decrece | Decrece |
Luego la función decrece en todo su dominio.
Anteriormente hemos visto que la función no tiene máximos ni mínimos, ya que su primera derivada no se anula.
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
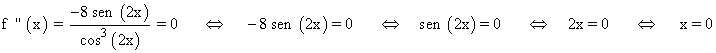
Tenemos que estudiar la curvatura dentro del primer periodo de la función, excepto en aquellos puntos en los que no está definida: (0 , π/4) , ( π/4 , π/2)
| Intervalo | (0 , π/4) | ( π/4 , π/2) |
|---|---|---|
| Punto de prueba | f '' ( π/6) < 0 | f '' ( π/3) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
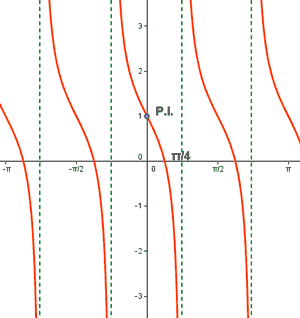
La función es cóncava hacia arriba o simplemente cóncava en ( π/4 , π/2) y cóncava hacia abajo o convexa en (0 , π/4) .
Punto de inflexión
De la tabla anterior se deduce que la función cambia de curvatura en el punto x = π/4 (pasa de ser convexa a ser cóncava) , pero hemos visto que dicho punto es una asíntota de la función. Por tanto, la función no tiene puntos de inflexión en (0 , π/2).
Sin embargo, la segunda derivada se anula en x = 0 , que observamos es un punto de inflexión, ya que hay un cambio de curvatura de cóncava a convexa.


 INICIO
INICIO