Discontinuidad de una función en un punto
Una función es discontinua en un punto a cuando no es continua en el, es decir, cuando no se cumple alguna de las tres condiciones de continuidad.
1) No existe el valor de la función en x = a , es decir, no existe f(a) .
2) No existe el límite de la función en x = a , es decir, no existe el límite de f(x) cuando x tiende a a .
3) Existe f(a) y el límite de f(x) en x = a pero son distintos:
![]()
Discontinuidad evitable
Una discontinuidad en x = a es evitable si existe el límite de la función f(x) en x = a y es finito, pero es distinto de la función en x = a o no existe el valor de la función en x = a .
Esta discontinuidad se llama evitable porque la función se convierte en continua al asignar el valor del límite al valor de la función en x = a :
![]()

![]()
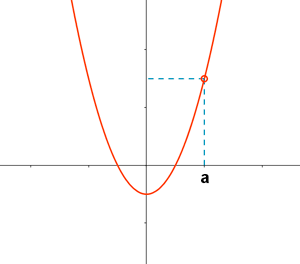
La función no está definida en x = a
Discontinuidad de 1ª especie o de salto
Una discontinuidad en x = a es de 1ª especie o de salto si existen los límites laterales y son distintos, o alguno de ellos es infinito.
Decimos que es de salto finito si los límites laterales son finitos y de salto infinito si alguno de ellos es infinito.
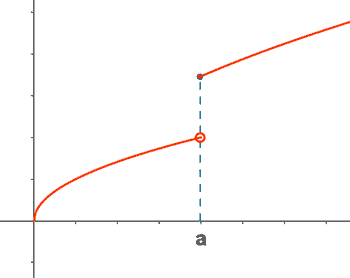
Discontinuidad de salto finito
Este tipo de discontinuidad ocurre cuando no existe el límite de f(x) cuando x tiende a a .
Es decir, aunque existen los límites laterales, estos no coinciden:
![]()
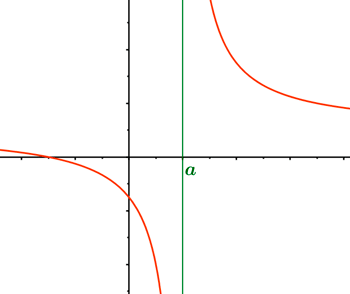
Discontinuidad de salto infinito
Los dos límites laterales en x = a son infinito.
![]()
![]()
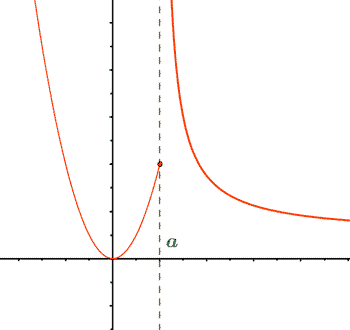
Discontinuidad de salto infinito
Uno de los dos límites laterales en x = a es infinito.
![]()
![]()
Discontinuidad de 2ª especie o dicontinuidad asintótica
Una discontinuidad en x = a es de 2ª especie si uno o los dos límites laterales no existen.
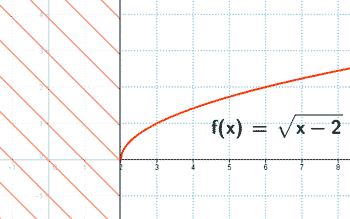
Discontinuidad de segunda especie
![]()
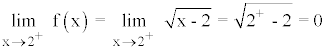
![]()


 INICIO
INICIO
