Ejercicios de representación de funciones polinómicas
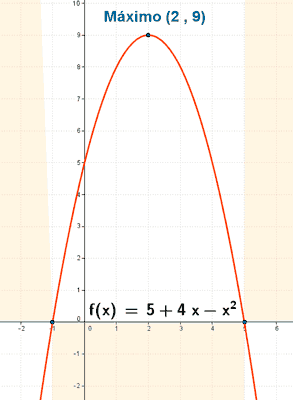
Representa gráficamente la función: y = 5 + 4x - x2
Función polinómica.
• Dom(f) = R = (-∞, +∞)
• Im(f) = R = (-∞, 9)
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función polinómica.
• Corte con el eje OX: f(x) = 0
5 + 4x - x2 = 0 ⇒ resolvemos la ecuación de segundo grado: x = -1 , x = 5
Los puntos de corte son: (-1, 0) y (5, 0)
• Corte con el eje OY: f(0)
f(0) = 5 + 4·0 - 02 = 5
El punto de corte es: (0, 5)
Como los puntos de corte con el eje OX son x = -1 y x = 5 , tenemos que estudiar los siguientes intervalos: (-∞, -1) , (-1, 5) , (5, +∞) :
| Intervalo | (-∞, -1) | (-1, 5) | (5, +∞) |
|---|---|---|---|
| Punto de prueba | f(-2) < 0 | f(0) > 0 | f(6) < 0 |
| Signo de f (x) | - | + | - |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
f(- x) = 5 + 4(-x) - (-x)2 = 5 - 4x - x2 ≠ f(x) ⇒ No es par.
f(- x) = 5 + 4(-x) - (-x)2 = 5 - 4x - x2≠ - f(x) ⇒ No es impar.
No es periódica porque las funciones polinómicas nunca lo son.
Asíntotas
Las funciones polinómicas no tienen asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = 4 - 2x = 0 ⇒ -2x = -4 ⇒ 2x = 4 ⇒ x = 2
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, 2) , (2, +∞)
| Intervalo | (- ∞, 2) | (2, +∞) |
|---|---|---|
| Punto de prueba | f ' (0) > 0 | f ' (3) < 0 |
| Signo de f ' (x) | + | - |
| Monotonía | Crece | Decrece |
Por el apartado anterior hemos obtenido un único punto que anula a la derivada primera (también llamado punto crítico) x = 2 , vamos a determinar a través de la segunda derivada si se trata de un máximo o de un mínimo.
Hallamos la derivada segunda: f '' (x) = - 2
• f '' (2) = - 6 < 0 ⇒ Hay un máximo en x = 2 ⇒ f(2) = 9 ⇒ Max (2, 9)
Como nuestra función es un polinomio de segundo grado el punto máximo obtenido coincide con el vértice de la parábola.
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = - 2 ≠ 0 para cualquier x ∈ R ⇒ no existen puntos de inflexión.
Como la función no tiene puntos de inflexión, la curvatura será igual en todo su dominio.
Veamos qué tipo de curvatura tiene:
| Intervalo | (-∞,+∞) |
|---|---|
| Punto de prueba | f '' (0) = - 2< 0 |
| Signo de f '' (x) | - |
| Curvatura | Convexa (∩) |
La función es cóncava hacia abajo o convexa en todo su dominio.
Punto de inflexión
En el apartado anterior hemos visto que la función no tiene puntos de inflexión.
Podemos comprobarlo también calculando la tercera derivada:
f '''(x) = 0 para cualquier x ∈ R
Como no existe ningún punto x para el que la tercera derivada no se anule, la función no tiene puntos de inflexión.
SELECTIVIDAD
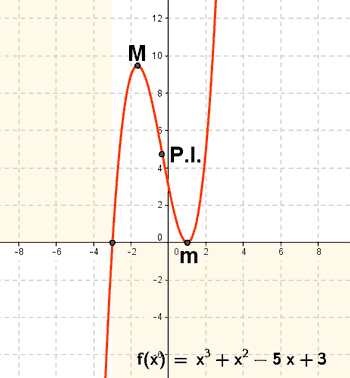
Representa gráficamente la función: y = x3 + x2 - 5x + 3
Función polinómica.
• Dom(f) = R = (-∞, +∞)
• Im(f) = R = (-∞, +∞)
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función polinómica.
• Corte con el eje OX: f(x) = x3 + x2 - 5x + 3 = 0
Intentamos resolver la ecuación aplicando Ruffini con los valores ±1 , ±3 .
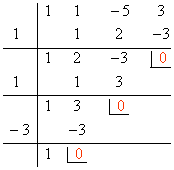
Tenemos dos soluciones: x = 1 (raíz doble) , x = - 3
Los puntos de corte son: (1, 0) y (-3, 0)
• Corte con el eje OY: f(0)
f(0) = 03 + 02 - 5·0 + 3= 3
El punto de corte es: (0, 3)
Como los puntos de corte con el eje OX son x = 1 y x = -3 , tenemos que estudiar los siguientes intervalos: (-∞, -3) , (-3, 1) , (1, +∞) :
| Intervalo | (-∞, -3) | (-3, 1) | (1, +∞) |
|---|---|---|---|
| Punto de prueba | f(-4) < 0 | f(0) > 0 | f(2) > 0 |
| Signo de f (x) | - | + | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
f(- x) =(-x)3 + (-x)2 - 5·(-x) + 3 =- x3 + x2 + 5x + 3 ≠ f(x) ⇒ No es par.
f(- x) = (-x)3 + (-x)2 - 5·(-x) + 3 =- x3 + x2 + 5x + 3≠ - f(x) ⇒ No es impar.
No es periódica porque las funciones polinómicas nunca lo son.
Asíntotas
Las funciones polinómicas no tienen asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = 3x2 + 2x - 5 = 0 ⇒ x = 1 y x = - 5/3
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, - 5/3) , (-5/3 , 1) , (1, +∞)
| Intervalo | (-∞, - 5/3) | (-5/3 , 1) | (1, +∞) |
|---|---|---|---|
| Punto de prueba | f ' (-2) > 0 | f ' (0) < 0 | f ' (2) > 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = -5/3 y x = 1 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = 6x + 2
• f '' (-5/3) = - 8 < 0 ⇒ Hay un máximo en x = -5/3 ⇒ f(-5/3) = 256/27 ⇒ Max (-5/3, 256/27)
• f '' (1) = + 8 > 0 ⇒ Hay un mínimo en x = 1 ⇒ f(1) = 0 ⇒ Min (1, 0)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = 6x + 2 = 0 ⇒ 6x = - 2 ⇒ x = -1/3
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, -1/3) , (-1/3, +∞) :
| Intervalo | (-∞, -1/3) | (-1/3, +∞) |
|---|---|---|
| Punto de prueba | f '' (-1) < 0 | f '' (0) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente concava en el intervalo (-1/3, +∞) y cóncava hacia abajo o convexa en el intervalo (-∞, -1/3) .
Punto de inflexión
Por el apartado anterior sabemos que el punto que anula a la derivada segunda es x = -1/3 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f '' (x) = 6x + 2 = 0 ⇒ 6x = - 2 ⇒ x = -1/3
f ''' (x) = 6 ≠ 0 ⇒ x = -1/3 es la abscisa del punto de inflexión ⇒ f(-1/3) = 88/27 ⇒ Punto inflexión (-1/3, 88/27)
SELECTIVIDAD
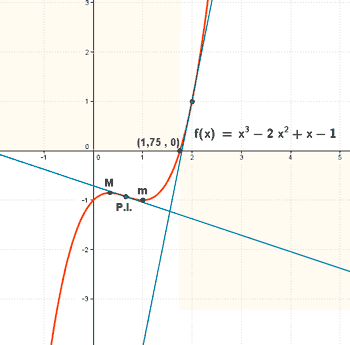
Dibujar la gráfica de la función f(x) = x3 - 2x2 + x - 1 ; hallar los máximos, mínimos y puntos de inflexión, y los puntos de ella en los que la pendiente de la tangente sea 5 .
Función polinómica.
• Dom(f) = R = (-∞, +∞)
• Im(f) = R = (-∞, +∞)
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función polinómica.
• Corte con el eje OX: f(x) = x3 - 2x2 + x - 1 = 0
Para encontrar un punto en el que la función corta al eje OX vamos a intentar aplicar el teorema de Bolzano.
Para ello probamos con distintos puntos para ver el signo de la función:
• Si x = 1 ⇒ f(1) = -1 < 0
• Si x = 2 ⇒ f(2) = 1 > 0
Por el teorema de Bolzano para funciones continuas, tenemos que existe un c ∈ (1 , 2) tal que f(c) = 0 , es decir, la función corta al eje OX en el intervalo (1 , 2) .
• Corte con el eje OY: f(0)
f(0) = 03 - 02 + 0 - 1= - 1
El punto de corte es: (0, - 1)
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = 3x2 - 4x + 1 = 0 ⇒ x = 1 y x = 1/3
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, 1/3) , (1/3 , 1) , (1, +∞)
| Intervalo | (-∞, 1/3) | (1/3, 1) | (1, +∞) |
|---|---|---|---|
| Punto de prueba | f ' (0) > 0 | f ' (1/2) < 0 | f ' (2) > 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 1/3 y x = 1 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = 6x - 4
• f '' (1/3) = -2 < 0 ⇒ Hay un máximo en x = 1/3 ⇒ f(1/3) = -23/27 ⇒ Max (1/3, -23/27)
• f '' (1) = + 2 > 0 ⇒ Hay un mínimo en x = 1 ⇒ f(1) = -1 ⇒ Min (1, -1)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = 6x - 4 = 0 ⇒ 6x = 4 ⇒ x = 2/3
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, 2/3) , (2/3, +∞) :
| Intervalo | (-∞, 2/3) | (2/3, +∞) |
|---|---|---|
| Punto de prueba | f '' (0) < 0 | f '' (1) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente concava en el intervalo (2/3, +∞) y concava hacia abajo o convexa en el intervalo (-∞, 2/3) .
Punto de inflexión
Por el apartado anterior sabemos que el punto que anula a la derivada segunda es x = 2/3 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f '' (x) = 6x - 4 = 0 ⇒ 6x = 4 ⇒ x = 2/3
f ''' (x) = 6 ≠ 0 ⇒ x = 2/3 es la abscisa del punto de inflexión ⇒ f(2/3) = - 25/27 ⇒ Punto inflexión (2/3, - 25/27)
Calculamos los puntos de la función en los que la pendiente de la tangente vale 5:
La pendiente de la tangente de una función se calcula hallando la primera derivada de la función.
Por tanto, la pendiente de la tangente valdrá 5 en aquellos puntos en los que la derivada primera de la función valga 5 .
f(x) = x3 - 2x2 + x - 1
f ' (x) = 3x2 - 4x + 1 = 5 ⇔ 3x2 - 4x + 1 - 5 = 0 ⇔ 3x2 - 4x - 4 = 0
Resolviendo la ecuación de segundo grado obtenemos los puntos que buscamos: x = - 2/3 , x = 2
f(2) = 1
f(-2/3) = -77/27
Luego los puntos son:
![]()
SELECTIVIDAD
Se considera la función f(x) = - x3 + bx2 + x + d .
a) Calcula razonadamente los valores de b y d para que la función f(x) tenga un máximo relativo en el punto (1 , 4) .
b) Suponiendo b = 1 y d = 3 , representa gráficamente la función f(x) en el intervalo [-2 , 2] .
a) Calcula razonadamente los valores de b y d para que la función f(x) tenga un máximo relativo en el punto (1 , 4) .
Como la función tiene que pasar por el punto (1 , 4), se tiene que cumplir que: f(1) = 4
f(1) = - 13 + b·1 + 1 + d = 4 ⇒ - 1 + b + 1 + d = 4 ⇒ b + d = 4
Como la función tiene un máximo relativo en el punto (1 , 4), la derivada primera en dicho punto tiene que ser 0:
f ' (x) = - 3x2 + 2bx + 1
f ' (1) = - 3·12 + 2b·1 + 1 = 0 ⇒ - 3 + 2b + 1 = 0 ⇒ 2b = - 1 + 3 = 2 ⇒ b = 1
Como ya sabemos el valor de b, podemos sustituir en la primera ecuación:
b + d = 4 ⇒ 1 + d = 4 ⇒ d = 3
b) Suponiendo b = 1 y d = 3 , representa gráficamente la función f(x) en el intervalo [-2 , 2] .
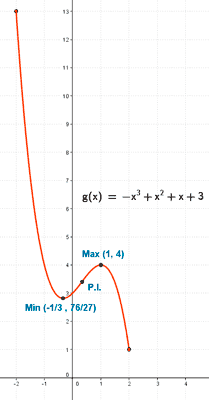
Si b = 1 y d = 3 , tenemos la función: f(x) = - x3 + x2 + x + 3
Para representarla gráficamente en el intervalo [-2 , 2] vamos a seguir los siguientes puntos:
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = - 3x2 + 2x + 1 = 0 ⇒ x = -1/3 , x = 1
Por lo tanto tenemos que estudiar los siguientes intervalos: (-2, -1/3) , (-1/3, 1) , (1 , 2)
| Intervalo | (-2, -1/3) | (-1/3, 1) | (1, 2) |
|---|---|---|---|
| Punto de prueba | f ' (-1) < 0 | f ' (0) > 0 | f ' (3/2) < 0 |
| Signo de f ' (x) | - | + | - |
| Monotonía | Decrece | Crece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = -1/3 y x = 1 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = - 6x + 2
• f '' (-1/3) = 4 > 0 ⇒ Hay un mínimo en x = -1/3 ⇒ f(-1/3) = 76/27 ⇒ Min (-1/3 , 76/27)
• f '' (1) = - 4 < 0 ⇒ Hay un máximo en x = 1 ⇒ f(1) = 4 ⇒ Max (1 , 4)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = - 6x + 2 = 0 ⇔ - 6x = - 2 ⇔ x = 1/3
Por lo tanto tenemos que estudiar los siguientes intervalos: (-2, 1/3) , (1/3, 2) :
| Intervalo | (-2, 1/3) | (1/3, 2) |
|---|---|---|
| Punto de prueba | f '' (0) = -2 > 0 | f '' (1) = -4 < 0 |
| Signo de f '' (x) | + | - |
| Curvatura | Cóncava(∪) | Convexa(∩) |
La función es cóncava hacia abajo o convexa en (1/3, 2) , y cóncava hacia arriba o simplemente cóncava en (-2, 1/3).
Punto de inflexión
Por el apartado anterior sabemos que el punto que anula a la derivada segunda es x = 1/3 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f '' (x) = - 6x + 2 = 0 ⇔ - 6x = - 2 ⇔ x = 1/3
f ''' (x) = -6 ≠ 0 ⇒ x = 1/3 es la abscisa del punto de inflexión ⇒ f(1/3) = 92/27 ⇒ Punto inflexión (1/3, 92/27)
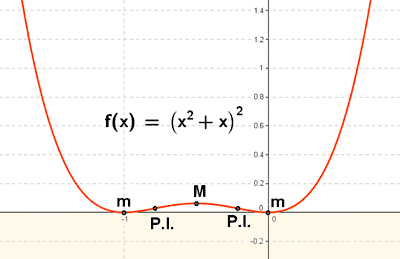
Representa gráficamente la función: y = (x2 + x)2
Función polinómica.
• Dom(f) = R = (-∞, +∞)
• Im(f) = (0, +∞)
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función polinómica.
• Corte con el eje OX: f(x) = 0
(x2 + x)2 = 0 ⇒ x2 + x = 0 ⇒ x(x + 1) = 0 ⇒ x = 0 , x = - 1
Los puntos de corte son: (0, 0) y (-1, 0)
• Corte con el eje OY: f(0)
f(0) = (02 + 0)2= 0
El punto de corte es: (0, 0)
Como los puntos de corte con el eje OX son x = 0 y x = -1 , tenemos que estudiar los siguientes intervalos: (-∞, -1) , (-1, 0) , (0, +∞) :
| Intervalo | (-∞, -1) | (-1, 0) | (0, +∞) |
|---|---|---|---|
| Punto de prueba | f(-2) > 0 | f(-1/2) > 0 | f(1) > 0 |
| Signo de f (x) | + | + | + |
Observamos que nuestra función está elevada al cuadrado, por tanto, siempre será positiva.
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
f(- x) =( (-x)2 - x)2 =(x2 - x)2 ≠ f(x) ⇒ No es par.
f(- x) = ( (-x)2 - x)2 =(x2 - x)2 ≠ - f(x) ⇒ No es impar.
No es periódica porque las funciones polinómicas nunca lo son.
Asíntotas
Las funciones polinómicas no tienen asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = 2(x2 + x)(2x + 1) = 0 ⇒ ⇒ x2 + x = 0 ó 2x + 1 = 0 ⇒ x = 0 , x = -1 y x = -1/2
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, - 1) , (-1 , -1/2) , (-1/2, 0) , (0 , +∞)
| Intervalo | (-∞, - 1) | (-1 , -1/2) | (-1/2, 0) | (0 , +∞) |
|---|---|---|---|---|
| Punto de prueba | f ' (-2) < 0 | f ' (-2/3) > 0 | f ' (1/3) < 0 | f ' (1) > 0 |
| Signo de f ' (x) | - | + | - | + |
| Monotonía | Decrece | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 0 , x = -1 y x = -1/2 vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = 2(2x + 1)(2x + 1) + 2(x2 + x)(2) = 12x2 + 12x + 2
• f '' (0) = 2 > 0 ⇒ Hay un mínimo en x = 0 ⇒ f(0) = 0 ⇒ Min (0, 0)
• f '' (-1) = 2 > 0 ⇒ Hay un mínimo en x = -1 ⇒ f(-1) = 0 ⇒ Min (-1, 0)
• f '' (-1/2) = -1 < 0 ⇒ Hay un máximo en x = -1/2 ⇒ f(-1/2) = 1/16 ⇒ Min (-1/2, 1/16)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = 12x2 + 12x + 2 = 0
![]()
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, -0,79) , (-0,79 , -0,21) , (-0,21 , +∞) :
| Intervalo | (-∞, -0,79) | (-0,79 , -0,21) | (-0,21 , +∞) |
|---|---|---|---|
| Punto de prueba | f '' (-1) > 0 | f '' (-1/2) < 0 | f '' (0) > 0 |
| Signo de f '' (x) | + | - | + |
| Curvatura | Concava (∪) | Convexa(∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente concava en el intervalo (-∞, -0,79)∪(-0,21 , +∞) y cóncava hacia abajo o convexa en el intervalo (-0,79 , -0,21) .
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = -0,79 y x = -0,21 , vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f '''(x) = 24x + 12
f ''' (-0,79) ≠ 0 ⇒ x = -0,79 es la abscisa del punto de inflexión ⇒ f(-0,79) = 0,03 ⇒ Punto inflexión (-0,79 , 0,03)
f ''' (-0,21) ≠ 0 ⇒ x = -0,21 es la abscisa del punto de inflexión ⇒ f(-0,21) = 0,03 ⇒ Punto inflexión (-0,21 , 0,03)
SELECTIVIDAD
Se considera la función de variable real:
![]()
Se pide: crecimiento o decrecimiento, extremos relativos, curvatura, puntos de inflexión y dibujo de su gráfica.
Función polinómica.
• Dom(f) = R = (-∞, +∞)
• Im(f) = (-∞, +∞)
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función polinómica.
• Corte con el eje OX: f(x) = 0
1/12(x5 - 80x) = 0 ⇒ x5 - 80x = 0 ⇒ x(x4 - 80) = 0
![]()
![]()
• Corte con el eje OY: f(0)
f(0) = 1/12(05 - 0)= 0
El punto de corte es: (0, 0)
f(- x) = 1/12 ( (-x)5 - 80(-x) ) = 1/12(- x5 + 80x) ≠ f(x) ⇒ No es par.
f(- x) = 1/12 ( (-x)5 - 80(-x) ) = 1/12(- x5 + 80x) = - 1/12(x5 - 80x) = - f(x) ⇒ Es impar.
La función tiene simetría impar, es decir, es simétrica respecto del origen.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
![]()
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, - 2) , (-2 , 2) , (2, +∞)
| Intervalo | (-∞, - 2) | (-2 , 2) | (2, +∞) |
|---|---|---|---|
| Punto de prueba | f ' (-3) > 0 | f ' (0) < 0 | f ' (3) > 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = -2 y x = 2 vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda:
![]()
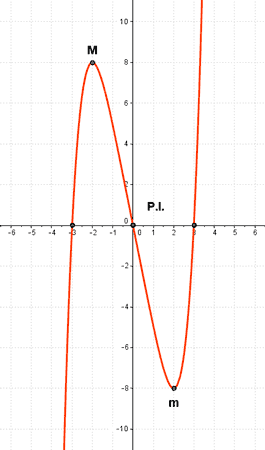
• f '' (-2) < 0 ⇒ Hay un máximo en x = -2 ⇒ f(-2) = 4 ⇒ Max (-2, 8)
• f '' (2) > 0 ⇒ Hay un mínimo en x = 2 ⇒ f(2) = -4 ⇒ Min (2, - 8)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, 0) , (0 , +∞) :
| Intervalo | (-∞, 0) | (0 , +∞) |
|---|---|---|
| Punto de prueba | f '' (-1) < 0 | f '' (1) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente concava en el intervalo (0 , +∞) y cóncava hacia abajo o convexa en el intervalo (-∞, 0) .
Punto de inflexión
Por el apartado anterior sabemos que el único punto que anula a la derivada segunda es x = 0 , vamos a determinar a través de la tercera derivada si se trata de un punto de inflexión.
![]()
f ''' (0) = 0 ⇒ como se anula, calculamos la siguiente derivada
![]()
f (4) (0) = 0 ⇒ como se anula, calculamos la siguiente derivada
![]()
f (5) (0) ≠ 0 ⇒ como estamos en una derivada impar (5) tenemos que x = 0 es la abscisa del punto de inflexión
f(0) = 0 ⇒ Punto inflexión (0 , 0)
Ver regla general para el cáculo del punto de inflexión


 INICIO
INICIO