Representación de funciones logarítmicas
Resumen de las propiedades de la función logaritmo neperiano
| 1 | La función logarítmica es la inversa de la exponencial: y = Ln x ⇔ x = ey |
|---|---|
| 2 | La función y = Ln x tiene por dominio { x ∈ R | x > 0 } y por recorrido R . |
| 3 | La función y = Ln x es continua, creciente e inyectiva en todo su dominio. |
| 4 | La función y = Ln x es convexa o cóncava hacia abajo en todo su dominio. |
| 5 | |
Representa gráficamente la función:
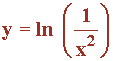
Función logarítmica.
Al tratarse de una función logarítmica tenemos que estudiar los valores que sean mayores que 0 y además los valores que anulan al denominador al ser racional:
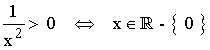
Al estar el denominador elevado al cuadrado, cualquier número menos el 0 cumple la condición:
• Dom(f) = R - {0} = (-∞, 0) ∪ (0, +∞)
Para hallar el recorrido de la función, invertimos las variables y calculamos el dominio de la variable y :
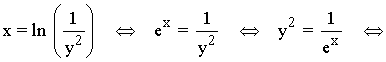
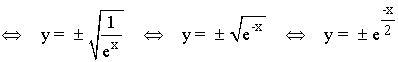
• Im(f) = R = (-∞, +∞)
Continuidad y tipos de discontinuidad
La función es continua en R - {0} , es decir, es discontinua en el punto x = 0
• Corte con el eje OX: f(x) = 0
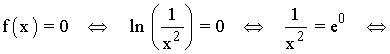
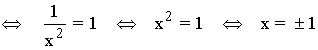
Los puntos de corte son: (-1, 0) y (1, 0)
• Corte con el eje OY: f(0)
La función no está definida en x = 0 , por lo tanto la función no corta al eje OY.
Como los puntos de corte con el eje OX son x = -1 y x = 1 y además la función es discontinua en el punto x = 0 , tenemos que estudiar los siguientes intervalos: (-∞, -1) , (-1, 0) , (0, 1) y (1, +∞) :
| Intervalo | (-∞, -1) | (-1, 0) | (0, 1) | (1, +∞) |
|---|---|---|---|---|
| Punto de prueba | f(-3) < 0 | f(-0,5) > 0 | f(0,5) > 0 | f(3) < 0 |
| Signo de f (x) | - | + | + | - |
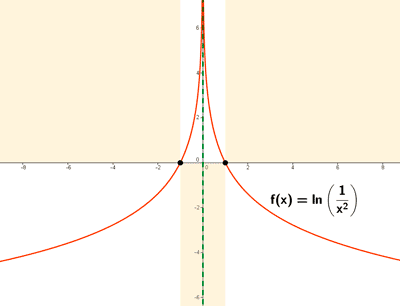
En la gráfica se marcan los puntos de corte con los ejes, los puntos de distintinuidad y las regiones donde no hay curva.
![]()
Por lo tanto la función es simétrica respecto al eje OY .
No es periódica porque las funciones logarítmicas nunca lo son.
Asíntotas
Donde se anula la característica del logarítmo:
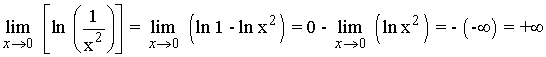
Por las características del logarítmo, sabemos que:
![]()
Es decir, existe una asíntota vertical en x = 0 .
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
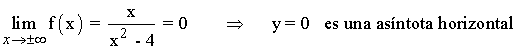
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
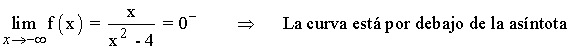
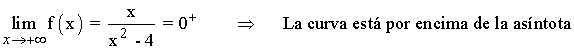
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
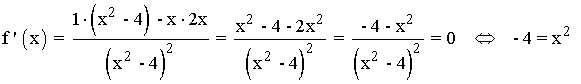
El numerador de la primera derivada no se anula para ningún valor, puesto que x2 ≠ -4 para cualquier valor de x .
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad sin incluir ninguno más puesto que no hay ningún valor que anule a la derivada primera: (-∞, -2) , (-2, 0) , (0, 2) , (2, +∞)
| Intervalo | (-∞, -2) | (-2, 0) | (0, 2) | (2, +∞) |
|---|---|---|---|---|
| Punto de prueba | f ' (-3) < 0 | f ' (-1) < 0 | f ' (1) < 0 | f ' (3) < 0 |
| Signo de f ' (x) | - | - | - | - |
| Monotonía | Decrece | Decrece | Decrece | Decrece |
Por el apartado anterior sabemos que ningún valor anula a la primera derivada, por lo tanto la función no tiene puntos críticos. Es decir, la función no tiene máximos ni mínimos.
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
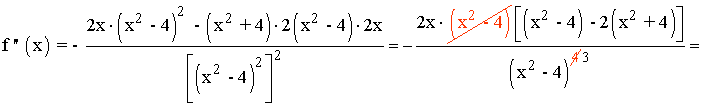
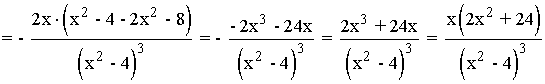
La segunda derivada se anula para x = 0 y 2x2 + 24 = 0
La segunda ecuación no tiene solución real, por lo tanto la segunda derivada solamente se anula para x = 0 .
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad incluyendo el valor que anula a la segunda derivada: (-∞, -2) , (-2, 0) , (0, 2) , (2, +∞)
| Intervalo | (-∞, -2) | (-2, 0) | (0, 2) | (0, +∞) |
|---|---|---|---|---|
| Punto de prueba | f '' (-3) < 0 | f '' (-1) > 0 | f '' (1) < 0 | f '' (3) > 0 |
| Signo de f '' (x) | - | + | - | + |
| Curvatura | Convexa (∩) | Concava (∪) | Convexa (∩) | Concava (∪) |
Punto de inflexión
Por el apartado anterior sabemos que el punto que anula a la derivada segunda es x = 0 y vamos a determinar a través de la tercera derivada si se trata de un punto de inflexión.
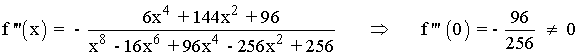
Por lo tanto x = 0 es la abscisa del punto de inflexión ⇒ f(0) = 0 ⇒ Punto inflexión (0, 0)


 INICIO
INICIO

