Ejercicios de representación de funciones racionales I
SELECTIVIDAD
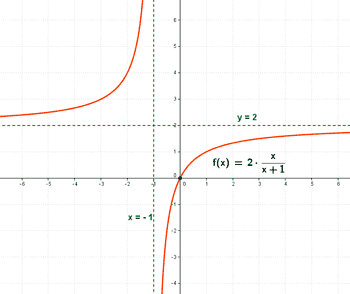
Dibujar la gráfica de la siguiente función indicando su dominio, intervalos de crecimiento y decrecimiento y asíntotas.
![]()
Función racional.
Al tratarse de una función racional tenemos que estudiar los valores que anulan al denominador para hallar el dominio:
x + 1 = 0 ⇔ x = - 1
Dom(f) = R - { - 1}
• Corte con el eje OX: f(x) = 0
![]()
El punto de corte es: (0, 0)
• Corte con el eje OY: f(0)
![]()
El punto de corte es: (0, 0)
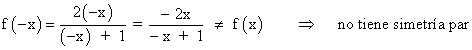
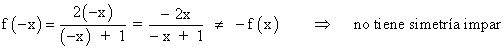
Por tanto la función no tiene simetría.
Asíntotas
Para hallar las asíntotas verticales tenemos que estudiar los valores que anulan al denominador y no anulan al numerador.
x + 1 = 0 ⇔ x = - 1 (este valor no anula al denominador)
Por tanto, la función tiene una asíntota vertical en x = - 1 .
Para estudiar la posición de la curva respecto a la asíntota vertical estudiamos los límites laterales:
![]()
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
![]()
![]()
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
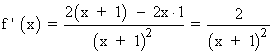
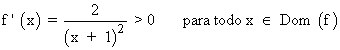
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad: (-∞ , -1) , (- 1 , +∞)
| Intervalo | (-∞ , -1) | (- 1 , +∞) |
|---|---|---|
| Punto de prueba | f ' (-2) > 0 | f ' (0) > 0 |
| Signo de f ' (x) | + | + |
| Monotonía | Crece | Crece |
Hemos visto anteriormente que la primera derivada no se anula en ningún valor, por tanto, la función no tiene máximos ni mínimos.
SELECTIVIDAD
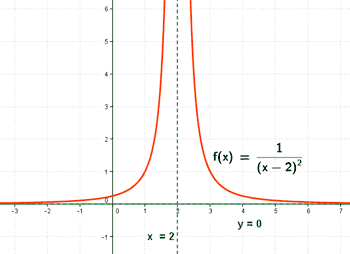
Estudiar y representar gráficamente la función:
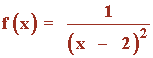
Función racional.
Al tratarse de una función racional tenemos que estudiar los valores que anulan al denominador para hallar el dominio:
(x - 2)2 = 0 ⇔ x - 2 = 0 ⇔ x = 2
Dom(f) = R - {2}
• Corte con el eje OX: f(x) = 0
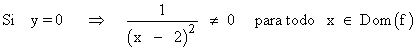
La función no corta al eje OX.
• Corte con el eje OY: f(0)
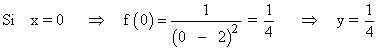
El punto de corte es: (0 , 1/4)
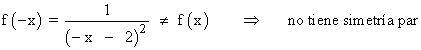
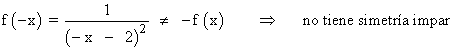
Por tanto la función no tiene simetría.
Asíntotas
Para hallar las asíntotas verticales tenemos que estudiar los valores que anulan al denominador y no anulan al numerador.
(x - 2)2 = 0 ⇔ x - 2 = 0 ⇔ x = 2 (no anula al numerador)
La función tiene una asíntota vertical en x = 2 .
Para estudiar la posición de la curva respecto a la asíntota vertical estudiamos los límites laterales:

Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
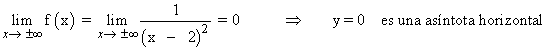
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
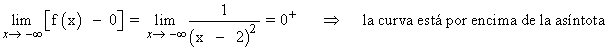
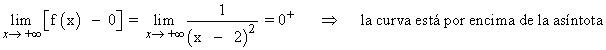
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
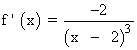
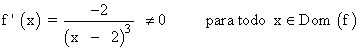
La derivada primera no se anula en ningún punto.
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad: (-∞ , 2) , (2 , +∞)
| Intervalo | (-∞ , 2) | (2 , +∞) |
|---|---|---|
| Punto de prueba | f ' (0) > 0 | f ' (3) < 0 |
| Signo de f ' (x) | + | - |
| Monotonía | Crece | Decrece |
Hemos visto anteriormente que la primera derivada no se anula en ningún valor, por tanto, la función no tiene máximos ni mínimos.
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
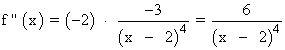
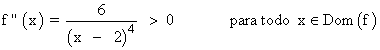
La derivada segunda no se anula en ningún valor.
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad: (-∞, 2) , (2, +∞)
| Intervalo | (-∞, 2) | (2, +∞) |
|---|---|---|
| Punto de prueba | f '' (0) > 0 | f '' (3) > 0 |
| Signo de f '' (x) | + | + |
| Curvatura | Concava (∪) | Concava (∪) |
Observamos que la derivada segunda siempre es positiva, por lo que podemos afirmar directamente que es cóncava en todo su dominio sin realizar la tabla.
Punto de inflexión
En el apartado anterior hemos visto que la segunda derivada no se anula para ningún valor de x, luego la función no tiene puntos de inflexión.
SELECTIVIDAD
Sea la función:
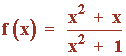
a) Calcula sus asíntotas.
b) Determina sus intervalos de crecimiento y decrecimiento.
c) Calcula sus máximos, mínimos y puntos de inflexión.
d) Dibuja la gráfica de la función con todos los datos obtenidos.
Función racional.
Al tratarse de una función racional tenemos que estudiar los valores que anulan al denominador para hallar el dominio:
Observamos que x2 + 1 > 0 , es decir, no existe ningún valor real que anule al denominador. Por tanto:
Dom(f) = R
• Corte con el eje OX: f(x) = 0
![]()
El punto de corte es: (0, 0) , (-1, 0)
• Corte con el eje OY: f(0)
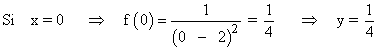
El punto de corte es: (0, 0)
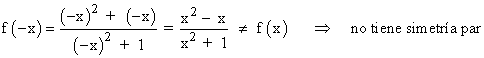
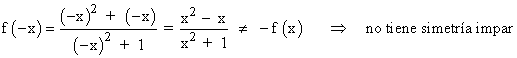
Por tanto la función no tiene simetría.
Asíntotas
Para hallar las asíntotas verticales tenemos que estudiar los valores que anulan al denominador y no anulan al numerador.
Hemos visto que no existen valores reales que anulen al denominador, por tanto, la función no tiene asíntotas verticales.
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
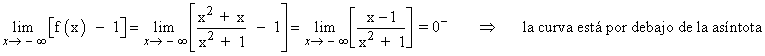
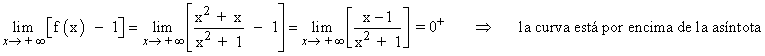
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
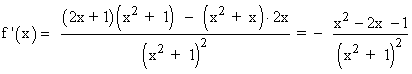
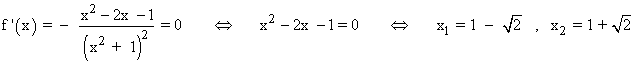
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞ , 1 - √2) , (1 - √2 , 1 + √2) , (1 + √2 , +∞)
| Intervalo | (-∞ , 1 - √2) | (1 - √2 , 1 + √2) | (1 + √2 , +∞) |
|---|---|---|---|
| Punto de prueba | f ' (-1) < 0 | f ' (0) > 0 | f ' (3) < 0 |
| Signo de f ' (x) | - | + | - |
| Monotonía | Decrece | Crece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 1 - √2 y x = 1 + √2 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
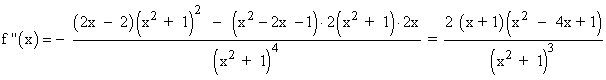
• f '' (1 - √2) > 0 ⇒ Hay un mínimo en x = 1 - √2 ⇒ f(1 - √2) = - 0,21 ⇒ Min (1 - √2, - 0,21)
• f '' (1 + √2) < 0 ⇒ Hay un máximo en x = 1 + √2 ⇒ f(1 + √2) = 1,21 ⇒ Max (1 + √2, 1,21)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
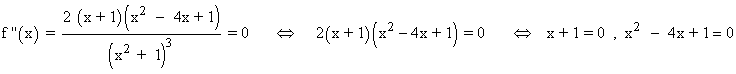
Resolviendo ambas ecuaciones, tenemos que la segunda derivada se anula para: x = -1 , x = 2 - √3 , x = 2 + √3
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, -1) , (-1, 2 - √3) , (2 - √3, 2 + √3) , (2 + √3, +∞)
| Intervalo | (-∞, -1) | (-1, 2 - √3) | (2 - √3, 2 + √3) | (2 + √3, +∞) |
|---|---|---|---|---|
| Punto de prueba | f '' (-2) < 0 | f '' (0) > 0 | f '' (1) < 0 | f '' (4) > 0 |
| Signo de f '' (x) | - | + | - | + |
| Curvatura | Convexa (∩) | Concava (∪) | Convexa (∩) | Concava (∪) |
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = -1 , x = 2 - √3 , x = 2 + √3.
En la tabla anterior hemos comprobado que la función tiene curvatura distinta antes y después de cada uno de dichos puntos (pasa de curvatura convexa a cóncava, y viceversa), por lo que se confirma que son puntos de inflexión.
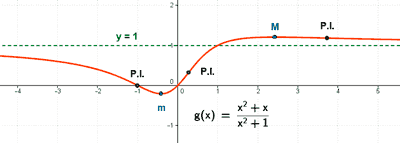
SELECTIVIDAD
Dada la siguiente función:
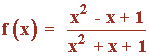
a) Estudia si existen y calcula, cuando sea posible, las asíntotas de la gráfica de f(x)
b) Determina los intervalos de crecimiento y decrecimiento, los extremos relativos y los valores que alcanza en ellos la función f(X)
c) Esboza la gráfica de f(x)
Función racional.
Al tratarse de una función racional tenemos que estudiar los valores que anulan al denominador para hallar el dominio: x2 + x + 1 = 0
La ecuación anterior no tiene soluciones reales, por lo tanto el dominio de la función es toda la recta real.
Dom(f) = R
• Corte con el eje OX: f(x) = 0
![]()
Por lo tanto la función no corta el eje OX .
• Corte con el eje OY: f(0)
![]()
El punto de corte es: (0, 1)
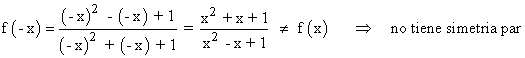
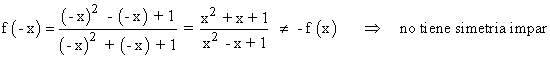
Por tanto la función no tiene simetría.
Asíntotas
Para hallar las asíntotas verticales tenemos que estudiar los valores que anulan al denominador y no anulan al numerador.
Hemos visto que no existen valores reales que anulen al denominador, por tanto, la función no tiene asíntotas verticales.
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
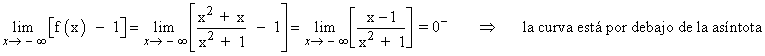
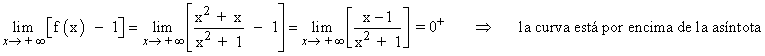
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
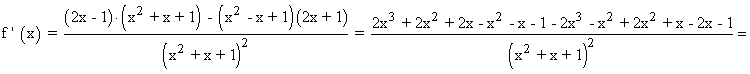
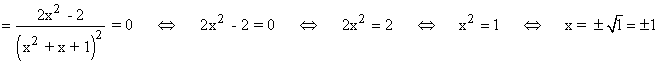
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad: (-∞ , -1) , (-1 , 1) , (1 , +∞)
| Intervalo | (-∞ , -1) | (-1 , 1) | (1 , +∞) |
|---|---|---|---|
| Punto de prueba | f ' (-2) > 0 | f ' (0) < 0 | f ' (2) < 0 |
| Signo de f ' (x) | + | - | + |
| Monotonía | Crece | Decrece | Crece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = -1 y x = +1.
• x = - 1 : la función crece en (-∞ , -1) y decrece en (-1 , +1) , por tanto tiene que ser un máximo relativo.
f(-1) = 3 ⇒ Máximo (-1, 3)
• x = +1 : la función decrece en (-1 , +1) y crece en (+1 , +∞) , por tanto tiene que ser un mínimo relativo.
f(+1) = 1/3 ⇒ Máximo (+1, 1/3)
SELECTIVIDAD
Dada la siguiente función, determinar razonadamente:
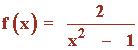
a) El dominio.
b) Los puntos de corte con los ejes de coordenadas.
c) Las ecuaciones de sus asíntotas, si es que las tiene.
d) Intervalos de crecimiento y de decrecimiento. Máximos y mínimos relativos.
e) Su representación gráfica.
Función racional.
Al tratarse de una función racional tenemos que estudiar los valores que anulan al denominador para hallar el dominio:
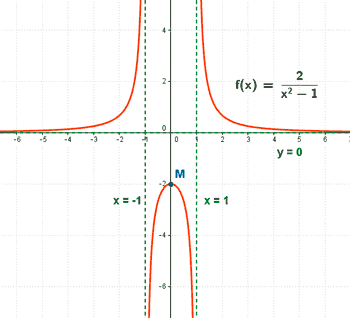
x2 - 1 = 0 ⇔ x2 = 1 ⇔ x = ± 1
Dom(f) = R - {-1 , +1}
• Corte con el eje OX: f(x) = 0
![]()
La función no corta al eje OX.
• Corte con el eje OY: f(0)
![]()
El punto de corte es: (0, -2)
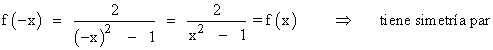
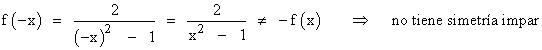
Por tanto la función es simétrica respecto del eje de ordenadas OY.
Asíntotas
Para hallar las asíntotas verticales tenemos que estudiar los valores que anulan al denominador y no anulan al numerador.
x2 - 1 = 0 ⇔ x2 = 1 ⇔ x = ± 1 (el numerador no se anula en dichos puntos)
La función tiene dos asíntotas verticales: x = -1 , x = 1
Para estudiar la posición de la curva respecto a la asíntota vertical estudiamos los límites laterales:
![]()
![]()
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
![]()
![]()
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
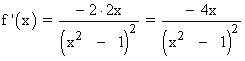
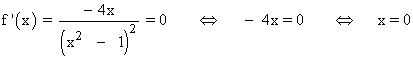
Por lo tanto tenemos que estudiar los siguientes intervalos de discontinuidad: (-∞ , -1) , (-1 , 0) , (0 , 1) , (1 , +∞)
| Intervalo | (-∞ , -1) | (-1 , 0) | (0 , 1) | (1 , +∞) |
|---|---|---|---|---|
| Punto de prueba | f ' (-2) > 0 | f ' (-1/2) > 0 | f ' (1/2) < 0 | f ' (2) < 0 |
| Signo de f ' (x) | + | + | - | - |
| Monotonía | Crece | Crece | Decrece | Decrece |
Por el apartado anterior sabemos que el único punto crítico o punto que anula a la derivada primera es x = 0. Observamos que la función cambia su monotonía en dicho punto (pasa de ser creciente a ser decreciente), por lo que x = 0 es un máximo relativo de la función.
SELECTIVIDAD
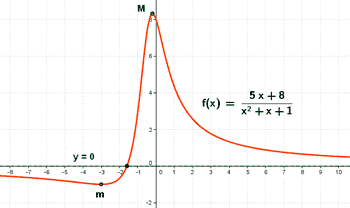
Calcula para la siguiente función:
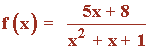
a) Su dominio, corte con los ejes, intervalos de crecimiento y decrecimiento, máximos y mínimos relativos.
b) Sus asíntotas.
c) Representación gráfica.
Función racional.
Al tratarse de una función racional tenemos que estudiar los valores que anulan al denominador para hallar el dominio.
Observamos que x2 + x + 1 > 0 , es decir, no existe ningún valor real que anule al denominador. Por tanto:
Dom(f) = R
• Corte con el eje OX: f(x) = 0
![]()
El punto de corte es: (-8/5 , 0)
• Corte con el eje OY: f(0)
![]()
El punto de corte es: (0, 8)
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
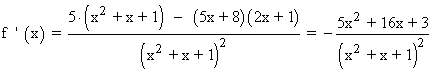
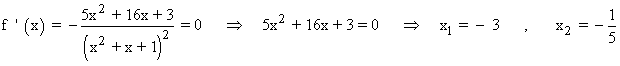
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, -3) , (-3, -1/5) , (-1/5, +∞)
| Intervalo | (-∞, -3) | (-3, -1/5) | (-1/5, +∞) |
|---|---|---|---|
| Punto de prueba | f ' (-4) < 0 | f ' (-1) > 0 | f ' (0) < 0 |
| Signo de f ' (x) | - | + | - |
| Monotonía | Decrece | Crece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = - 3 y x = -1/5 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
• x = - 3 : la función decrece en (-∞ , -3) y crece en (-3 , -1/5) , por tanto tiene que ser un mínimo relativo.
• x = -1/5 : la función crece en (-3 , -1/5) y decrece en (-1/5 , +∞) , por tanto tiene que ser un máximo relativo.
Asíntotas
Para hallar las asíntotas verticales tenemos que estudiar los valores que anulan al denominador y no anulan al numerador.
Pero hemos visto anteriormente que el denominador no se anula para ningún valor real, por tanto, la función no tiene asíntotas verticales.
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
![]()
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
![]()
![]()
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.


 INICIO
INICIO