Ejercicios de representación de funciones con valor absoluto
Sea la función: f(x) = | x | + | x - 2 |
a) Expresa f(x) como una función definida a trozos
b) Dibuja la gráfica de f(x)
c) Escribe el intervalo abierto de la recta real formado por los puntos en los que f(x) es derivable y se anula su derivada
a) Expresa la función f(x) como una función definida a trozos
Estudiamos cada valor absoluto por separado:
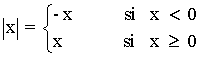
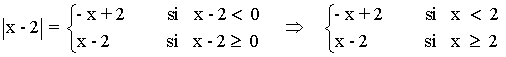
A continuación, estudiamos la suma de los valores de |x| y |x - 2| en los tres intervalos que se generan: (-∞ 0) , (0, 2) y (2, +∞) .
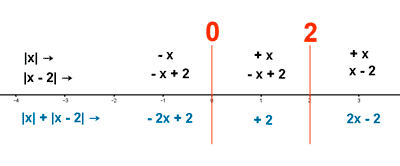
Por lo tanto la función queda definida de la siguiente forma:
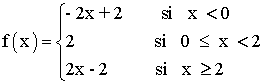
b) Dibuja la gráfica de f(x).
Las funciones que definen a f son polinómicas, por lo que son continuas en todo R , y en particular, lo son en sus intervalos de definición.
Estudiamos la continuidad de f en los puntos de unión: x = 0 , x = 2
• x = 0
f(0) = 2
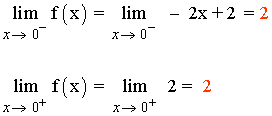
Como los límites laterales coinciden, el límite cuando x → 0 existe y además:
![]()
Luego la función es continua en x = 0 .
• x = 2
f(2) = 2·2 - 2 = 2
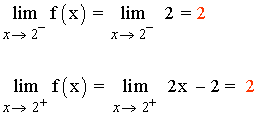
Como los límites laterales coinciden, el límite cuando x → 2 existe y además:
![]()
Luego la función es continua en x = 2 .
Por tanto, la función f es continua en todo R .
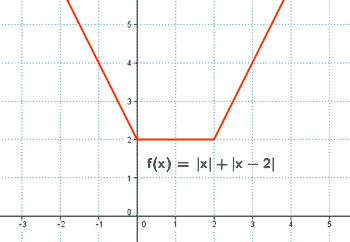
c) Escribe el intervalo abierto de la recta real formado por los puntos en los que f(x) es derivable y se anula su derivada.
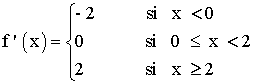
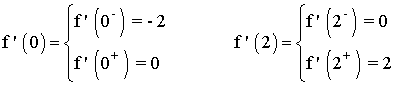
Por lo tanto f(x) es derivable en toda la recta real exceptuando los puntos x = 0 y x = 2 , es decir f(x) es derivable en R - {0, 2} .
Por otra parte, tenemos que f(x) sea derivable y f ' (x) = 0 en el intervalo (0, 2).
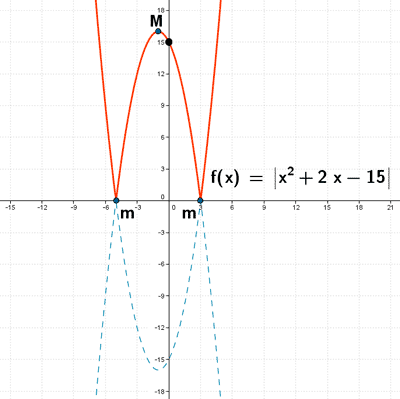
Sea la función: f(x) = | x2 + 2x - 15 |
a) Expresa f(x) como una función definida a trozos
b) Dibuja la gráfica de f(x)
c) Determina los puntos en que no es derivable la función
a) Expresa la función f(x) como una función definida a trozos
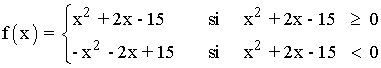
Para definir la función, tenemos que resolver la siguiente ecuación: x2 + 2x - 15 = 0
Las raíces de la ecuación son x = 3 y x = -5 , es decir, tenemos que estudiar como se comporta la función en los siguientes intervalos: (-∞, -5) , (-5, 3) y (3, +∞)
| Intervalo | (-∞, -5) | (-5, 3) | (3, +∞) |
|---|---|---|---|
| Punto de prueba | f(-6) > 0 | f(0) < 0 | f(4) > 0 |
| Signo de f (x) | + | - | + |
Por lo tanto la función queda definida de la siguiente forma:
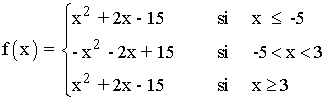
b) Dibuja la gráfica de f(x).
Las funciones que definen a f son polinómicas, por lo que son continuas en todo R , y en particular, lo son en sus intervalos de definición.
A continuación vamos a calcular los puntos de corte:
• Corte con el eje OX: f(x) = 0
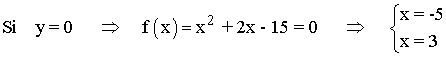
Los puntos de corte son: (-5, 0) y (3, 0)
• Corte con el eje OY: f(0)
![]()
El punto de corte es: (0, 15)
Además, la función tiene un eje de simetría para x = - b / 2a . Es decir, x = -1 .
Para x = -1 tenemos que f(-1) = 16 . Por lo tanto el vértice es el punto V (-1, 16) .
c) Determina los puntos en que no es derivable la función.
La función es continua y derivable al tratarse de funciones polinómicas, por lo que tenemos que estudiar únicamente los puntos de unión.
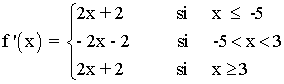
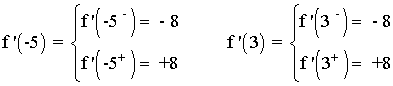
Por lo tanto f(x) es derivable en toda la recta real exceptuando los puntos x = -5 y x = 3 , es decir f(x) es derivable en R - {-5, 3} .
SELECTIVIDAD
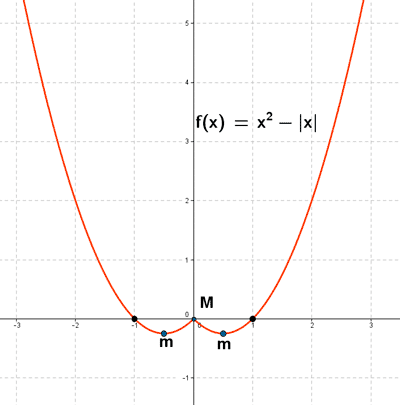
Sea la función: f(x) = x2 - | x |
a) Estudia la derivabilidad de f(x)
b) Determina los intervalos de crecimiento y decrecimiento de f(x)
c) Calcula los extremos relativos de f(x)
d) Representa la función
a) Estudia la derivabilidad de f(x)
Para estudiar la derivabilidad de la función, en primer lugar vamos a expresarla como una función a trozos:
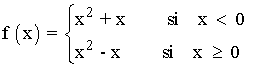
Al tratarse de funciones polinómicas, son continuas y derivables en todo su dominio, por lo tanto únicamente estudiamos el punto de unión x = 0 :
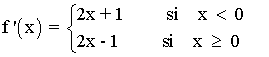
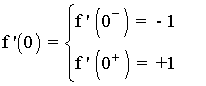
Por lo tanto, la función es continua en todo R y derivable en R - {0}
b) Determina los intervalos de crecimiento y decrecimiento de f(x)
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
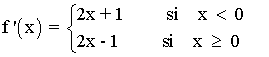
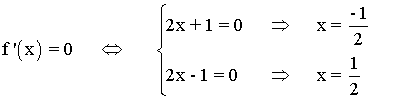
Por lo tanto tenemos que estudiar los siguientes intervalos (incluyendo el punto de unión de las dos ramas de la función): (-∞ , -1/2) , (-1/2 , 0), (0 , 1/2) , (1/2 , +∞)
| Intervalo | (-∞ , -1/2) | (-1/2, 0) | (0, 1/2) | (1/2 , +∞) |
|---|---|---|---|---|
| Punto de prueba | f ' (-1) < 0 | f ' (-1/4) > 0 | f ' (1/4) > 0 | f ' (1) > 0 |
| Signo de f ' (x) | - | + | - | + |
| Monotonía | Decrece | Crece | Decrece | Crece |
c) Calcula los extremos relativos de f(x)
Hemos visto anteriormente que la primera derivada se anula en x = -1/2 y x = 1/2.
Además, estudiamos también el punto x = 0 al cambiar la función de rama en dicho punto:
• x = -1/2 : La función pasa de decreciente a creciente ⇒ Min (-1/2, -1/4)
• x = +1/2 : La función pasa de decreciente a creciente ⇒ Min (+1/2, -1/4)
• x = 0 : La función pasa de creciente a decreciente ⇒ Max (0, 0)
La función es continua en x = 0 pero no es derivable. Además, antes de x = 0 la función crece y despues decrece, por lo tanto la función presenta un máximo relativo en el punto (0, 0), en el que no es derivable.
d) Representa la función
SELECTIVIDAD
Sea la función: f(x) = x | x - 4 |
a) Estudia la continuidad de f(x)
b) Estudia la derivabilidad en x = 4
c) Representa la función
a) Estudia la continuidad de f(x)
Definimos la función f por trozos:
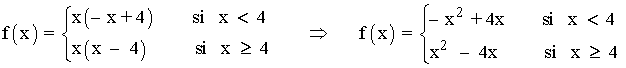
Las funciones que definen a f son polinómicas, por lo que son continuas en todo R y particular, lo son en sus respectivos intervalos de definición. Por tanto, la función f es continua en: (-∞ , 4) ∪ (4 , ∞)
Veamos la continuidad en el punto de unión: x = 4
x = 4
f(4) = 42 - 4·4 = 0
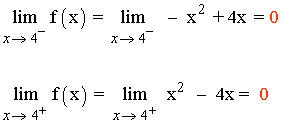
Como los límites laterales coinciden, el límite cuando x → 4 existe y además:
![]()
Luego la función f es continua en todo R .
b) Estudia la derivabilidad en x = 4
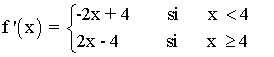
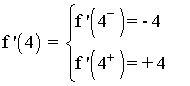
Por lo tanto la función no es derivable en x = 4 .
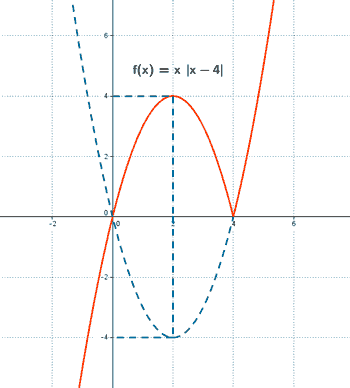
c) Representa la función
Hallamos los puntos de corte con los ejes:
• Si x = 0 : y = f(0) ⇒ y = 0 ⇒ (0 , 0)
• Si y = 0 : - x2 + 4x = 0 ⇒ x(- x + 4) = 0 ⇒ x = 0 ó x = 4 ⇒ (0 , 0) , (4 , 0)
x2 - 4x = 0 ⇒ x(x - 4) = 0 ⇒ x = 0 ó x = 4 ⇒ (0 , 0) , (4 , 0)
Ambas ramas de f son funciones polinómicas de segundo grado, por lo que son parábolas. Para dibujarlas vamos a calcular sus respectivos vértices:
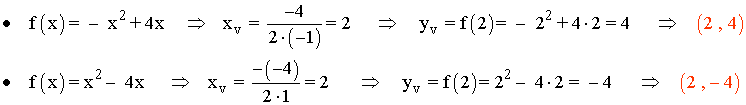
SELECTIVIDAD
Sea la función:
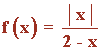
a) Indica el dominio de la función
b) Indica las asíntotas y su posición relativa
c) Indica los intervalos de crecimiento y decrecimiento
d) Representa la función
a) Indica el dominio de la función
Antes de nada, definimos la función f por trozos:
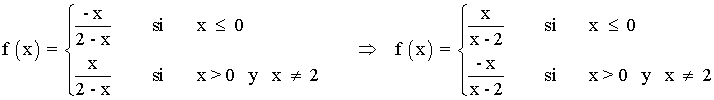
Las funciones que definen a f son racionales, por lo que son continuas excepto en los puntos que se anula el denominador. Por tanto, la función f es continua en: (-∞ , 2) ∪ (2 , ∞)
Dom (f) = R - {2}
b) Indica las asíntotas y su posición relativa
• Asíntotas verticales:
La recta x = 2 es una asíntota vertical, puesto que se verifica que:
![]()
• Asíntotas horizontales:
Para calcular las asíntotas horizontales tenemos que calcular el límite en el infinito:
![]()
![]()
• Asíntotas horizontales:
Como la función tiene asíntotas horizontales, no puede tener asíntotas oblicuas.
c) Indica los intervalos de crecimiento y decrecimiento
Para calcular los intervalos de crecimiento y decrecimiento tenemos que calcular la primera derivada e igualarla a 0.
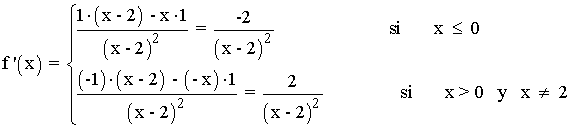
Como la primera derivada no se anula, estudiamos los intervalos definidos por los puntos de discontinuidad y donde la función cambia de trozo o rama: x = 0 y x = 2
| Intervalo | (-∞, 0) | (0, 2) | (2, +∞) |
|---|---|---|---|
| Punto de prueba | f ' (-1) < 0 | f ' (1) > 0 | f ' (3) > 0 |
| Signo de f ' (x) | - | + | + |
| Monotonía | Decrece | Crece | Crece |
Como la función es continua en x = 0 (pero no derivable) y en dicho punto cambia de decreciente a creciente, la función tiene un mínimo relativo en el punto (0, 0) .
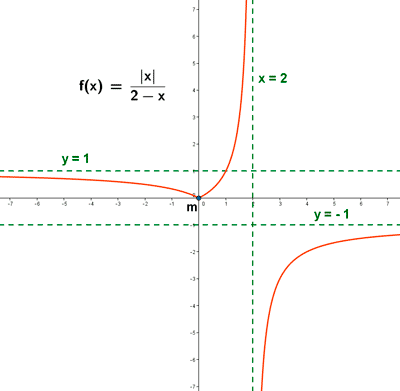
d) Representa la función
SELECTIVIDAD
Sea la función: f(x) = x2 + | x - 2 |
a) Estudia la continuidad de f(x)
b) Estudia la derivabilidad en x = 2
c) Representa la función
a) Estudia la continuidad de f(x)
Definimos la función f por trozos:
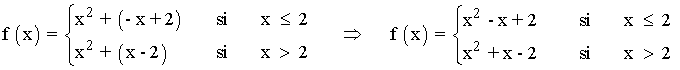
Las funciones que definen a f son polinómicas, por lo que son continuas en todo R y particular, lo son en sus respectivos intervalos de definición.
Veamos la continuidad en el punto de unión: x = 2
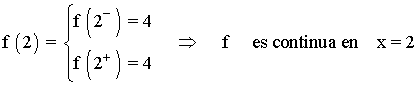
Es decir, la función es continua en x =2 , por lo tanto es continua en toda la recta real: Dom(f) = R
b) Estudia la derivabilidad en x = 2
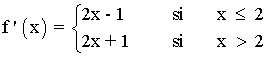
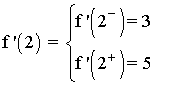
Por lo tanto la función no es derivable en x = 2 .
c) Representa la función
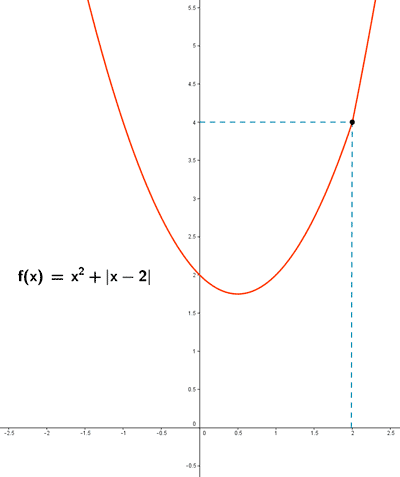
SELECTIVIDAD
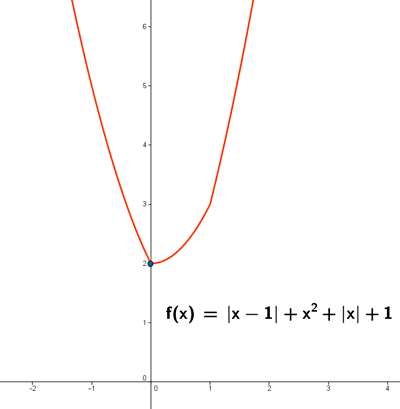
Sea la función: f(x) = | x - 1 | + x2 + | x | + 1
a) Expresa f(x) como una función definida a trozos
b) Estudia la derivabilidad en x = 0 y x = 1
c) Representa la función
a) Expresa f(x) como una función definida a trozos
Al tratarse de una función definida como la suma de sumandos con valor absoluto, tenemos que estudiar los intervalos determinados por las soluciones de dichos sumandos:
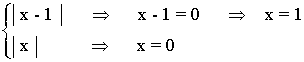
| Intervalo | (-∞, 0) | (0, 1) | (1, +∞) |
|---|---|---|---|
| |x - 1| | - x + 1 | - x + 1 | x - 1 |
| x2 | x2 | x2 | x2 |
| |x| | -x | +x | +x |
| +1 | +1 | +1 | +1 |
| |x - 1|+x2+|x|+1 | x2 - 2x + 2 | x2 + 2 | x2 + 2x |
Por lo tanto, nuestra función queda definida de la siguiente manera:
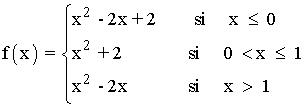
b) Estudia la derivabilidad en x = 0 y x = 1
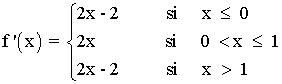
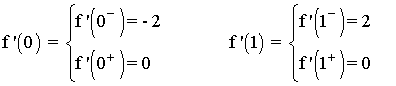
Al no coincidir los límites laterales, tenemos que la función no es derivable en x = 0 y tampoco en x = 1
c) Representa la función
SELECTIVIDAD
Sea la función:
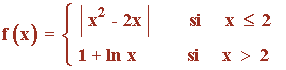
a) Expresa f(x) como una función definida a trozos
b) Estudia los intervalos de crecimiento y decrecimiento
c) Estudia la curvatura de la función f(x)
d) Representa gráficamente la función f(x)
e) Obtener la gráfica de y = f(x+2)
a) Expresa f(x) como una función definida a trozos
Una de las ramas de la función posee un valor absoluto, así que hay que estudiar los intervalos determinados por las soluciones de dichos sumandos:
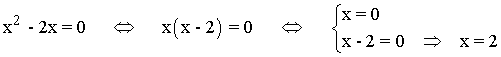
Por lo tanto, la primera rama de la función se expresa de la siguiente manera:
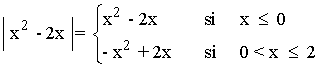
Es decir, la función original se define a trozos de la siguiente manera:
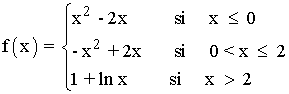
b) Estudia los intervalos de crecimiento y decrecimiento
Para estudiar la monotonía de la función vamos a diferenciar los intervalos de definición:
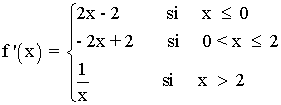
• (-∞, 0) ⇒ f ' (x) = 0 ⇔ 2x - 2 = 0 ⇔ 2x = 2 ⇔ x = 1∉ (-∞, 0)
• (0, 2) ⇒ f ' (x) = 0 ⇔ - 2x + 2 = 0 ⇔ 2x = 2 ⇔ x = 1
• (2, +∞) ⇒ f ' (x) = 1/x ≠ 0 para cualquier valor de x
Por lo tanto, tenemos que estudiar el signo de la primera derivada en los siguientes intervalos: (-∞, 0) . (0, 1) , (1, 2) y (2, +∞)
| Intervalo | (-∞, 0) | (0, 1) | (1, 2) | (2, +∞) |
|---|---|---|---|---|
| Punto de prueba | f ' (-1) < 0 | f ' (0,5) > 0 | f ' (1,5) < 0 | f ' (3) > 0 |
| Signo de f ' (x) | - | + | - | + |
| Monotonía | Decrece | Crece | Decrece | Crece |
La función es continua en x = 0 y pasa de decreciente a creciente, por lo tanto, existe un mínimo relativo en (0, 0) .
La función es continua en x = 1 y cambia de creciente a decreciente, luego existe un máximo relativo en (1, 1) .
c) Estudia la curvatura de la función f(x)
Para estudiar la curvatura tenemos que igualar la segunda derivada a 0.
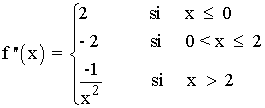
• (-∞, 0) ⇒ f '' (x) > 0 para cualquier valor de x
• (0, 2) ⇒ f '' (x) < 0 para cualquier valor de x
• (2, +∞) ⇒ f '' (x) < 0 para cualquier valor de x
Como la segunda derivada no se anula para ningún valor, estudiamos los siguientes intervalos: (-8, 0) . (0, 2) y (2, +8)
| Intervalo | (-∞, 0) | (0, 2) | (2, +∞) |
|---|---|---|---|
| Punto de prueba | f '' (-1) > 0 | f ' (1) < 0 | f ' (3) < 0 |
| Signo de f '' (x) | + | - | - |
| Curvatura | Cóncava (∪) | Convexa (∩) | <Convexa (∩) |
d) Representa gráficamente la función f(x)
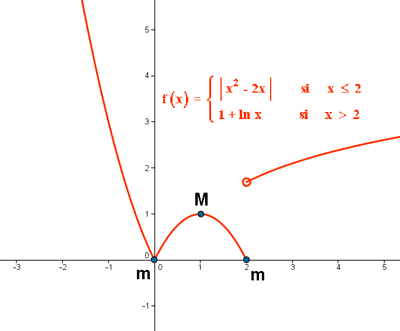
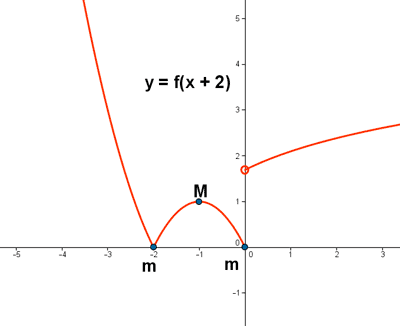
e) Obtener la gráfica de y = f(x+2)
La función y = f(x + 2) es una traslación de la función y = f(x) dos unidades hacia la izquierda.


 INICIO
INICIO