Asíntotas oblicuas
Asíntotas oblicuas lineales
Una función f(x) tiene una asíntota oblicua en y = mx + n si:
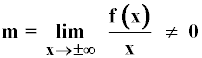
![]()
Para conocer la posición de la curva respecto de la asíntota oblicua se hallan:
![]()
Asíntotas oblicuas:
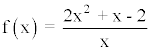
Para hallar las asíntotas oblicuas calculamos:
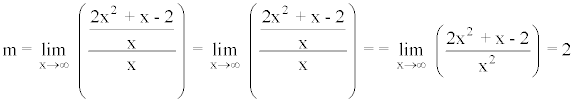
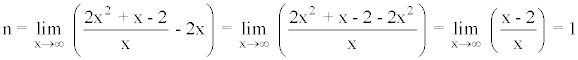
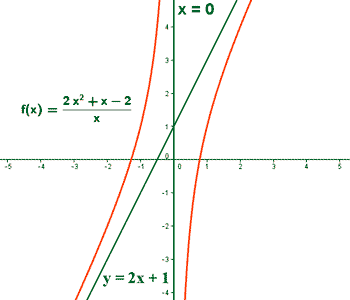
Calculamos la posición de la curva respecto a la asíntota oblicua:
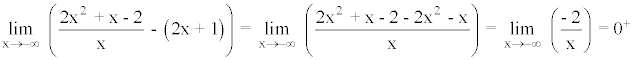
La curva está encima de la asíntota oblicua.
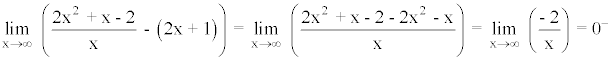
La curva está por debajo de la asíntota oblicua.
Método general para hallar las asíntotas oblicuas
Para hallar una asíntota oblicua se hace la división del numerador entre el denominador, siendo el cociente la fórmula de la asíntota.
Caso I: Asíntota oblicua lineal
Si grado de P(x) - grado de Q(x) = 1
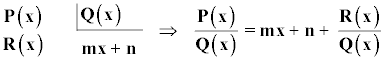
La recta y = mx + n es asíntota oblicua si se cumple alguna de la siguientes condiciones:
![]()
Para calcular la posición de la curva respecto de las asíntotas oblicuas, hallamos:
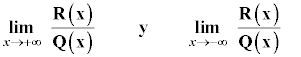
Si el límite da 0+ (cero por la derecha) la gráfica de la función se encuentra por encima de la asíntota. Si el límite da 0- (cero por la izquierda) la gráfica de la función se encuentra por debajo de la asíntota.
Podemos calcular la asíntota oblicua del ejemplo anterior por este método:
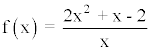
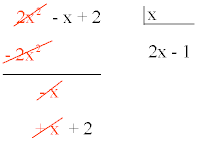
Por lo tanto, la asíntota oblicua es: y = 2x - 1
Caso II: Asíntota oblicua no lineal o ramas parabólicas
Si grado de P(x) - grado de Q(x) ≥ 2
En este caso hay una asíntota oblicua no lineal o rama parabólica, donde se cumple que:
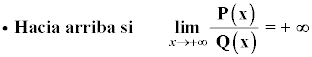
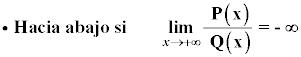
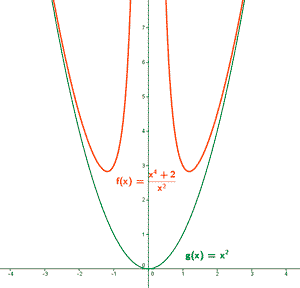
• Asíntota oblicua:
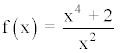
Para calcular la asíntota realizamos la división entre el numerador y el denominador:
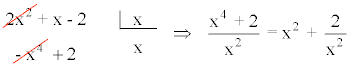
Por lo tanto, existe una rama parabólica (asíntota oblicua no lineal): y = x2
Resumen
Una función racional puede tener asíntotas verticales, horizontales y oblicuas:
1) Tiene tantas asíntotas verticales como raíces reales distintas tenga el denominador y que no lo sean del numerador.
2) Tiene una asíntota horizontal si el grado del numerador es menor o igual que el del denominador.
3) Tiene una asíntota oblicua si el grado del numerador es uno más que el del denominador.
4) Tiene una rama parabólica (asíntota oblicua no lineal) si el grado del numerador es 2 o más que el del denominador.
Una función racional puede tener varias asíntotas verticales, y a lo sumo una horizontal u oblicua. Si la tiene horizontal, no la tiene oblicua y viceversa.


 INICIO
INICIO
