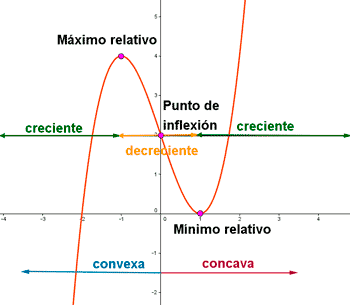
Concavidad y convexidad y puntos de inflexión
Una función derivable se dice que es cóncava hacia arriba o simplemente concava (∪) en x = a si la recta tangente a la gráfica de la función en ese punto está por debajo de ella.
Una función derivable se dice que es cóncava hacia abajo o convexa (∩) en x = a si la recta tangente a la gráfica de la función en ese punto está por encima de ella.
El punto (a, f(a)) es un punto de inflexión de la función f(x) si la función cambia de curvatura, es decir, pasa de ser concava a convexa o viceversa.
Criterio de concavidad y convexidad
Si la función f(x) es derivable dos veces en el intervalo (a, b) :
• f(x) es concava hacia arriba o concava en (a, b) ⇔ f '' (x) > 0 en todo x∈(a, b)
• f(x) es concava hacia abajo o convexa en (a, b) ⇔ f '' (x) < 0 en todo x∈(a, b)
• f(x) es lineal en (a, b) ⇔ f '' (x) = 0 en todo x∈(a, b)
Criterio de inflexión
Si (a, f(a)) es un punto de inflexión de f(x) , derivable dos veces, entonces f '' (a) = 0 y f ''' (a) ≠ 0 .
Procedimiento para hallar la concavidad y convexidad
Estudia los intervalos de concavidad y convexidad de la siguiente función: f(x) = x3 - 3x + 2
1) Se hallan los puntos que anulan a la segunda derivada.
Calculamos la segunda derivada de la función.
f ' (x) = 3x2 - 3 ⇒ f '' (x) = 6x
A continuación calculamos las raíces de la segunda derivada.
6x = 0 ⇔ x = 0
Por lo tanto la segunda derivada se anula en x = 0 .
2) Se hallan las discontinuidades.
La función f(x) es continua en todo R, luego no tiene discontinuidades.
3) Se representan en la recta real los puntos que anulan a la segunda derivada y las discontinuidades.
Se prueba un punto de cada uno de los intervalos de la segunda derivada. Solamente se considera el signo.
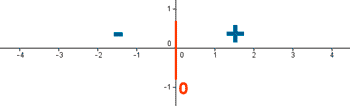
• f '' (-1) = -6 < 0
• f '' (+1) = +6 > 0
4) Se escriben los intervalos de concavidad y convexidad:
• Si f '' (x) > 0 es concava.
• Si f '' (x) < 0 es convexa.
En nuestro caso tenemos que:
• f(x) es concava en el intervalo (0, +∞)
• f(x) es convexa en el intervalo (-∞, 0)
Procedimiento para hallar los puntos de inflexión
1) Se calcula la segunda derivada: f '' (x)
Calculamos la segunda derivada de la función.
f ' (x) = 3x2 - 3 ⇒ f '' (x) = 6x
2) Se resuelve la ecuación: f '' (x) = 0
A continuación calculamos las raíces de la segunda derivada.
6x = 0 ⇔ x = 0
Por lo tanto la segunda derivada se anula en x = 0 .
3) Se sustituye las raíces de la segunda derivada en la función inicial y se obtienen los posibles puntos de inflexión.
f(0) = 2
4) Se halla la tercera derivada: f ''' (x)
Se sustituyen las abscisas de los posibles puntos de inflexión en la tercera derivada:
Si f ''' (x) ≠ 0 son puntos de inflexión.
f ''' (x) = 6 ≠ 0 ⇒ El punto (0, 2) es un punto de inflexión.


 INICIO
INICIO

