Funciones crecientes y decrecientes
Una función f(x) es creciente sobre un intervalo si para cualesquiera dos números x1 y x2 en el intervalo, x1 < x2 implica que f(x1) < f(x2) .
Una función f(x) es decreciente sobre un intervalo si para cualesquiera dos números x1 y x2 en el intervalo, x1 < x2 implica que f(x1) > f(x2) .
Criterio de crecimiento y decrecimiento
Sea f(x) una función que es continua en el intervalo [a, b] y derivable en el intervalo abierto (a, b) . Entonces ocurre que:
1) Si f ' (x) > 0 para todo x ∈(a, b) , entonces f(x) es creciente en el intervalo [a, b] .
2) Si f ' (x) < 0 para todo x ∈(a, b) , entonces f(x) es decreciente en el intervalo [a, b] .
3) Si f ' (x) = 0 para todo x ∈(a, b) , entonces f(x) es constante en el intervalo [a, b] .
Un punto crítico o singular es un punto en el que la primera derivada se anula. Un punto crítico puede ser un máximo o un mínimo relativo o un punto de inflexión.
Procedimiento para hallar el crecimiento y decrecimiento de una función
Estudia los intervalos de crecimiento y decrecimiento de la siguiente función: f(x) = x3 - 3x + 2
1) Se hallan los puntos críticos, es decir, los puntos que anulan a la primera derivada.
Calculamos la primera derivada de la función.
f ' (x) = 3x2 - 3
A continuación calculamos las raíces de la primera derivada.
3x2 - 3 = 0 ⇔ 3x2 = 3 ⇔ x2 = 1 ⇔ x = ±1
Por lo tanto la primera derivada se anula en x = -1 y x = 1 .
2) Se hallan las discontinuidades.
La función f(x) es continua en todo R, luego no tiene discontinuidades.
3) Se representan en la recta real los puntos críticos y las discontinuidades.
Se prueba un punto de cada uno de los intervalos de la primera derivada. Solamente se considera el signo.
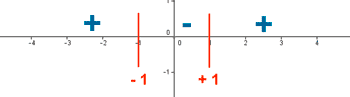
• f ' (-2) = 3·(-2)2 - 3 = 12 - 3 = 9 > 0
• f ' (0) = 3·02 - 3 = - 3 < 0
• f ' (+2) = 3·(+2)2 - 3 = 12 - 3 = 9 > 0
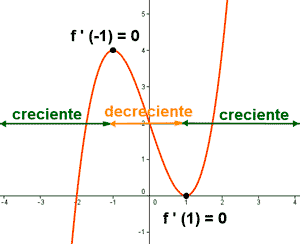
4) Se escriben los intervalos de crecimiento: f ' (x) > 0 en el intervalo (-∞, -1) ∪ (1, +∞)
Se escriben los intervalos de decrecimiento: f ' (x) < 0 en el intervalo (-1, 1)


 INICIO
INICIO

