Problemas resueltos sobre edades
1) Cuatro hermanos tienen juntos 50 años. Hallar sus edades respectivas sabiendo que cada uno tiene 3 años más que el que le sigue en edad.
Sea x la edad del primer hermano.
El segundo hermano tendrá: x + 3
El tercero tendrá: x + 3 + 3 = x + 6
El cuarto tendrá: x + 3 + 3 + 3 = x + 9
La suma de las cuatro edades es 50, luego:
x + (x + 3) + (x + 6) + (x + 9) = 50
Resolvemos la ecuación:
x + (x + 3) + (x + 6) + (x + 9) = 50 ⇔ 4x + 18 = 50 ⇔ 4x = 32 ⇔ x = 8
Si el primer hermano tiene x = 8 años los demás tendrán: 11 , 14 , 17
2) En una familia la suma de las edades de los 4 hijos es 65 años. ¿Cuál es la edad de cada uno si el mayor tiene 3 años más que el segundo, el segundo 4 años más que el tercero, y éste 2 más que el pequeño?
Sea x la edad del hijo menor (cuarto hijo).
El tercero tiene 2 años más que el cuarto: x + 2
El segundo tiene 4 años más que el tercero: (x + 2) + 4 = x + 6
El primero tiene 3 años más que el segundo: (x + 6) + 3 = x + 9
La suma de las cuatro edades es 65, luego:
x + (x + 2) + (x + 6) + (x + 9) = 65
Resolvemos:
x + (x + 2) + (x + 6) + (x + 9) = 65 ⇔ 4x + 17 = 65 ⇔ 4x = 48 ⇔ x = 12
Si x = 12 ⇒ x + 2 = 14 , x + 6 = 18 , x + 9 = 21
Las edades son 12, 14, 18 y 21.
1) La edad de Pedro es el doble de la edad de Luis y dentro de 6 años será de 5/3. ¿Cuáles son sus edades?
Llamaremos a la edad de Luis 'x'.
Edades actuales Dentro de 6 años
Pedro 2x 2x + 6
Luis x x + 6
Planteamos la ecuación:
![]()
La resolvemos:
3(2x + 6) = 5(x + 6) ⇔ 6x + 18 = 5x + 30 ⇔ 6x - 5x = 30 - 18 ⇔ x = 12
Si Luis tiene x = 12 años ⇒ Pedro tiene 2x = 2·12 = 24 años.
Luis tiene 12 y Pedro tiene 24 años.
2) La edad de Salvador es triple que la de su hijo Francisco, y hace 6 años sólo era el doble. Calcular la edad actual de cada uno.
Sean x la edad de Francisco.
Edades actuales Hace 6 años
Salvador 3x 3x - 6
Francisco x x - 6
Hace 6 años, la edad de Salvador era el doble de la de su hijo, luego:
3x - 6 = 2(x - 6)
Resolvemos la ecuación:
3x - 6 = 2(x - 6) ⇒ 3x - 6 = 2x - 12 ⇒ 3x - 2x = - 12 + 6 ⇒ x = - 6
No es posible tener una edad negativa, y como ésta es la única solución de la ecuación, el problema no tiene solución. Por tanto, es imposible que se cumplan las condiciones del problema.
1) La edad actual de Marta es el triple de la de su hijo Juan. Halla las edades de ambos sabiendo que dentro de 16 años la madre tendrá doble edad que el hijo.
Sea x la edad de Marta e y la edad de su hijo Juan.
Edades actuales Dentro de 6 años
Marta x x + 16
Juan y y + 16
La edad de Marta, x , es el triple de la de su hijo: x = 3y
Dentro de 16 años, la madre tendrá doble edad que su hijo: (x + 16) = 2(y + 16)
Reuniendo ambas ecuaciones tenemos el siguiente sistema:
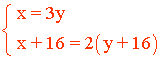
Lo resolvemos por el método de sustitución, pues ya tenemos la variable x despejada en la primera ecuación. Primero simplificamos la segunda ecuación, después, sustituimos por x = 3y:
x + 16 = 2(y + 16) ⇒ x + 16 = 2y + 32 ⇒ x - 2y = 32 - 16 ⇒ x - 2y = 16
x - 2y = 16 ⇒ 3y - 2y = 16 ⇒ y = 16
Si y = 16 ⇒ x = 3y = 3·16 = 48
Por tanto, Marta tiene 48 años y su hijo Juan 16.
2) Hace 5 años la edad de Alicia era el triple de la de Claudia, y dentro de 5 años sólo será el doble. ¿Qué edad tiene cada uno de ellos?
Sean x e y las edades de Alicia y Claudia respectivamente.
Edades actuales Hace 5 años Dentro de 5 años
Alicia x x - 5 x + 5
Claudia y y - 5 y + 5
Planteamos el sistema con dos ecuaciones:
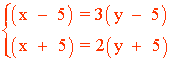
Antes de resolverlo simplificamos el sistema:
(x - 5) = 3(y - 5) ⇒ x - 5 = 3y - 15 ⇒ x - 3y = - 10
(x + 5) = 2(y + 5) ⇒ x + 5 = 2y + 10 ⇒ x - 2y = 5
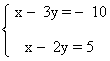
Resolvemos el sistema por el método de reducción; a la primera ecuación le restamos la segunda:
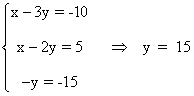
Si y = 15 , despejando la variable x en la segunda ecuación tenemos: x - 2y = 5 ⇒ x = 5 + 2y = 5 + 2·15 = 35
Luego Alicia tiene 35 y Claudia tiene 15.
La suma de las edades de un padre y sus dos hijos es 73 años. Dentro de 10 años la edad del padre será el doble de la edad del hijo menor. Hace 12 años la edad del hijo mayor era el doble de la edad de su hermano. ¿Cuál es la edad actual de cada uno?
Sean x , y , z las edades del padre, del hijo mayor y del hijo menor, respectivamente.
Edades actuales Dentro de 10 años Hace 12 años
Padre x x + 10 x - 12
Hijo mayor y y + 10 y - 12
Hijo menor z z + 10 z - 12
La suma de sus edades es 73: x + y + z = 73
Dentro de 10 años el padre tendrá el doble de edad que su hijo menor: (x + 10) = 2(z + 10)
Hace 12 años, el hermano mayor tenía el doble de edad que su hermano: (y - 12) = 2(z - 12)
Reuniendo las ecuaciones:
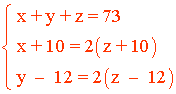
Simplificando el sistema obtenemos el siguiente:
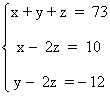
Despejamos las variables x e y en la segunda y tercera ecuación respectivamente, y después sustituimos en la primera:
x - 2z = 10 ⇔ x = 10 + 2z
y - 2z = -12 ⇔ y = 2z - 12
x + y + z = 73 ⇒ (10 + 2z) + (2z - 12) + z = 73 ⇒ 5z - 2 = 73 ⇒ 5z = 75 ⇒ z = 15
Si z = 15 ⇒ x = 10 + 2z = 10 + 2·15 = 40
Si z = 15 ⇒ y = 2z - 12 = 2·15 - 12 = 18
Por tanto, el padre tiene 40 años, su hijo mayor 18 y su hijo menor 15.


 INICIO
INICIO