Problemas resueltos de trabajo
Planteamiento general de un problema de trabajo:
Supongamos que tenemos 2 obreros y un trabajo a realizar.
• En una hora, el primer obrero hace 1/t1 del trabajo.
• En una hora, el segundo obrero hace 1/t2 del trabajo.
En una hora, los dos obreros juntos habrán hecho 1/T:
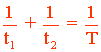
Dos obreros necesitan 18 días para terminar juntos una obra. Sabiendo que separados, uno de ellos necesita 15 días más que el otro, averiguar cuánto tiempo invertirá cada obrero en terminar la obra trabajando por separado.
Sea t1 = x los días que necesita el primer obrero. Entonces, en un día habrá hecho: 1/t1 = 1/x
Si el segundo tarda 15 días más que el primero: x + 15
Por tanto, en un día habrá hecho: 1/(x + 15)
Por otro lado, si entre los dos obreros tardan en hacer la obra 18 días, en un día harán: 1/18
Aplicamos la fórmula general a los datos que tenemos:
![]()
Resolvemos la ecuación aplicando: m.c.m.(x, x + 15) = x(x + 15)
![]()
Quitamos denominadores:
18 (x + 15 + x ) = x(x + 15) ⇔ 18(2x + 15) = x2 + 15x ⇔ 36x + 270 = x2 + 15x ⇔ x2 - 21x - 270 = 0
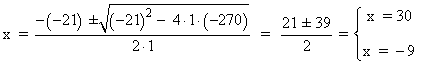
Descartamos x = -9 , ya que el tiempo no puede ser negativo.
Luego si x = 30, entonces: x + 15 = 45
El primer obrero tarda 30 días y el segundo 45 días.
Dos obreros tienen que hacer una obra. Haciendo cada uno la mitad tardan 25/2 horas, pero trabajando juntos hacen el trabajao en 6 horas. ¿Cuánto tardaría uno solo en hacer toda la obra?
Sea t1 = x el tiempo que tarda el primer obrero en hacer la obra completa. En una hora hará: 1/t1 = 1/x
Pero si hace la mitad de la obra, tardará: x/2
Sea t2 = y el tiempo que tarda el segundo obrero en hacer la obra completa. En una hora hará: 1/t2 = 1/y
Pero si hace la mitad de la obra, tardará: y/2
Si trabajan la mitad de la obra, tenemos la ecuación:
![]()
Si hacen la obra completa tardan 1/6 horas, por tanto:
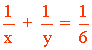
Sustituimos por y = 25 - x y resolvemos:
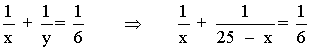
Aplicamos: m.c.m.(x, 25 - x) = x(25 - x)
![]()
![]()
![]()
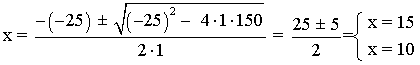
Si x = 15 ⇒ y = 25 - x = 10
Si x = 10 ⇒ y = 25 - 10 = 15
Tardarán 15 horas y 10 horas respectivamente.


 INICIO
INICIO