Problemas resueltos sobre Cifras
Hallar un número de dos cifras, tal que si se invierte el orden de éstas, el número que resulta se diferencia del primitivo en 18 unidades. Las cifras del número que se pide suman 12 unidades.
Llamaremos a dichas cifras 'x' e 'y' , por lo que el número que buscamos será xy.
Las cifras suman 12 unidades: x + y = 12
El número xy está formado por y unidades y x decenas.
Sabemos que las x decenas son 10·x unidades.
Por tanto, podemos escribir el número xy como: y + 10x unidades
El problema nos dice que si invertimos el orden de las cifras, el número resultante se diferencia del original en 18 unidades, esto es:
Invertimos las cifras: xy = y + 10x ⇒ yx = x + 10y
Su diferencia es 18: xy - yx = 18 ⇔ (y + 10x) - (x + 10y) = 18
Tenemos el siguiente sistema de ecuaciones:
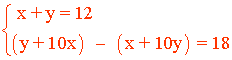
Lo resolvemos mediante el método de sustitución.
Despejamos x en la primera ecuación y sustituimos en la segunda:
x + y = 12 ⇔ x = 12 - y
(y + 10x) - (x + 10y) = 18 ⇔ y + 10x - x - 10y = 18 ⇔ 9x - 9y = 18 ⇔ dividimos entre 9, x - y = 2
x - y = 2 ⇔ (12 - y) - y = 2 ⇔ 12 - y - y = 2 ⇔ - 2y = - 10 ⇔ y = 5
Si y = 5 ⇒ x = 12 - y = 12 - 5 = 7
El número que buscamos es: xy = 75
Hallar un número de dos cifras sabiendo que la suma de éstas es 10 y que el doble del número que resulta de invertir las cifras supera en una unidad a dicho número.
Sea 'x' la cifra de las decenas del número buscado.
Sea 'y' la cifra de las unidades del número buscado.
La suma de dichas cifras es 10: x + y = 10
Entonces, el número puede escribirse: xy = 10x + y
Si invertimos las cifras tenemos: yx = 10y + x
El doble del número con las cifras invertidas supera en una unidad al número original: 2yx = xy + 1 ⇔ 2(10y + x) = (10x + y) + 1
Reuniendo ambas ecuaciones tenemos el siguiente sistema:
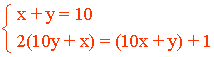
Lo resolvemos por el método de sustitución: despejamos la variable x en la primera ecuación y sustituimos en la segunda:
x + y = 10 ⇔ x = 10 - y
2(10y + x) = (10x + y) + 1 ⇔ 20y + 2x = 10x + y + 1 ⇔ 19y - 8x = 1
19y - 8x = 1 ⇒ 19y - 8(10 - y) = 1 ⇒ 19y - 80 + 8y = 1 ⇒ 27y = 81 ⇒ y = 3
Si y = 3 ⇒ x = 10 - y = 10 - 3 = 7
El número que buscamos es: xy = 73
La suma de las tres cifras de un número es 16. La suma de la primera y tercera es igual a la segunda; y si se permutan entre si las cifras de las unidades y de las decenas, el número resultante es 27 unidades menor que el propuesto. ¿Cuál es éste?
Sea xyz el número que buscamos. Tiene z unidades, y decenas y x centenas.Por tanto, podemos escribirlo como: xyz = z + 10y + 100x
La suma de las tres cifras es 16: x + y + z = 16
La suma de la primera y la tercera es la segunda: z + x = y
Permutamos las cifras de las unidades y de las decenas: xzy = y + 10z + 100x
El número resultante es 27 unidades menor que el original: xzy = xyz - 27 ⇔ (y + 10z + 100x) = (z + 10y + 100x) - 27
Reuniendo las tres ecuaciones tenemos el siguiente sistema:
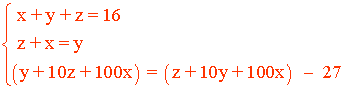
Simplificamos el sistema:
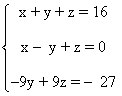
Vamos a aplicar el método de reducción en las dos primeras ecuaciones, le restamos a la primera la segunda ecuación:
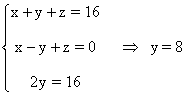
Si y = 8 , por la tercera ecuación del sistema tenemos:
-9y + 9z = -27 ⇒ -9·8 + 9z = -27 ⇒ 9z = -27 + 72 ⇒ 9z = 45 ⇒ z = 5
Si y = 8 , z = 5 , despejando la variable x en la segunda ecuación tenemos:
x - y + z = 0 ⇒ x = y - z = 8 - 5 = 3
Luego el número que buscamos es: xyz = 385
Se tienen dos factores en un producto, uno de ellos posee dos cifras, si a este factor se le disminuye la suma de sus cifras, el producto total se reduce a la mitad ¿Cuál es este factor?
Sea xy el factor de dos cifras, y z el segundo factor del producto.
Reducir el primer factor en la suma de sus cifras es: xy - (x + y)
El producto entre los nuevos factores reduce a la mitad el producto original, es decir:
![]()
Eliminamos z en ambos miembros de la igualdad, ya que es factor común en ellos; y "pasamos" el 2 multiplicando al otro miembro (o lo que es lo mismo, multiplicamos por 2 en ambos miembros):
2 [xy - (x + y)] = xy ⇔ 2xy - 2(x - y) = xy 2xy - xy = 2(x + y) ⇔ xy = 2(x + y)
Sabemos que xy es un número con y unidades y x decenas, por tanto: xy = 10x + y
Sustituimos el valor de xy en la primera ecuación:
xy = 2(x + y) ⇒ 10x + y = 2x + 2y ⇒ 8x = y
Como y es un dígito, debe ser un número entre 0 y 9.
Si x = 2 ⇒ 8x = y ⇒ 8·2 = 16 = y , no puede ser. Tampoco será válido para un valor de x mayor que 2.
Si x = 1 ⇒ 8x = y ⇒ 8·1 = 8 = y , sí es válido.
El primer factor es: xy = 18


 INICIO
INICIO