Problemas resueltos de móviles
- 1. Móviles con el mismo sentido
- 2. Móviles con sentidos opuestos
- 3. Móviles con retraso en el tiempo
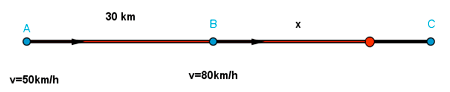
Dos coches salen al mismo tiempo. El primero sale desde un punto A y el segundo desde un punto B, y se dirigen hacia un punto C en la misma dirección. Sabiendo que la distancia de A a B es 30 Km, y que el primer coche va a 80 Km/h y el segundo a 50 km/h, ¿a qué distancia de B se encontrarán? ¿qué tiempo tardarán en encontrarse?
La ecuación del movimiento rectilíneo uniforme es:
e = espacio recorrido
e = v · t v = velocidad
t = tiempo
El primer coche va desde A hasta C, por lo que recorrerá una distancia de: 30 + x
Sustituyendo por los datos que sabemos en la ecuación del movimiento: 30 + x = 80 · t
Para el caso del segundo coche, sabemos que va desde B hasta C, por lo que la distancia recorrida es x. Sustituyendo: x = 50 · t
Por tanto, tenemos el siguiente sistema de ecuaciones:
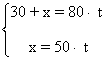
Resolveremos el sistema mediante el método de igualación.
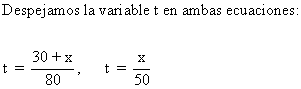
Igualamos ambas ecuaciones y calculamos x:
(30 + x)/80 = x/50 ⇔ 50 (30 + x) = 80x ⇔ 1500 + 50x = 80x ⇔ 1500 = 30x ⇔ x = 50 Km
La distancia entre el punto B y el punto C es 50 Km.
Como x = 50 Km ⇒ t = x/50 = 50/50 = 1 h
Tardan 1 hora en encontrarse.
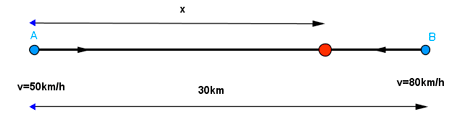
Dos coches salen al mismo tiempo en sentidos opuestos. El primero sale desde un punto A y el segundo desde un punto B, y se dirigen uno al encuentro del otro. Sabiendo que distancia entre A y B es de 30 Km, y que el primer coche va a una velocidad de 80 Km/h y el segundo a 50 Km/h, ¿a qué distancia se encontrarán? ¿cuánto tardarán en encontrarse?
La ecuación del movimiento rectilíneo uniforme es:
e = espacio recorrido
e = v · t v = velocidad
t = tiempo
El primer coche recorre una distancia x a una velocidad de 80 Km/h.
Sustituyendo por los datos que sabemos en la ecuación del movimiento: x = 80 · t
Si el primer coche recorre x kilómetros, el segundo recorrerá: 30 - x
Por tanto, el segundo recorre 30 - x kilómetros a 50 Km/h. Sustituyendo: 30 - x = 50 · t
Nos queda el siguiente sistema de ecuaciones lineales:
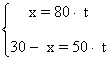
Lo resolvemos mediante el método de igualación.
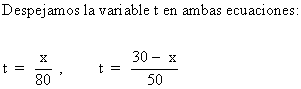
Igualamos y calculamos x:
x/80 = (30 - x)/50 ⇔ 50x = 80 (30 - x) ⇔ 50x = 2400 - 80x ⇔ 50x + 80x = 2400 ⇔ 130x = 2400 ⇔ x = 18,23 Km
Se encuentran a 18,23 Km de A.
Si x = 18,23 Km ⇒ t = x/80 = 18,23/80 = 0,227875 h
Calculamos cuántos minutos y segundos son 0,227875 horas:
Si 1 hora tiene 60 minutos, entonces: 0,227875 · 60 = 13,6725 min.
Si 1 minuto tiene 60 segundos, entonces: 0,6725 · 60 = 40,35 seg.
Se encontrarán trascurridos: 13 min 40 seg.
Dos coches están situados en un punto A. El primero de ellos sale a una velocidad de 50 Km/h. Media hora mas tarde sale el segundo a 80 Km/h en el mismo sentido. ¿En qué punto alcanzará el segundo coche al primero? ¿cuánto tardará en alcanzarlo?
La ecuación del movimiento rectilíneo uniforme es:
e = espacio recorrido
e = v · t v = velocidad
t = tiempo
Puesto que ambos salen desde el mismo punto, la distancia que recorrerán hasta encontrarse será la misma. La llamaremos 'x'.
El primer coche recorre una distancia x en un tiempo t y a una velocidad de 50 Km/h, luego: x = 50 · t
Ahora, si el primer coche se mueve durante un tiempo t, el segundo se moverá durante: t - (1/2)
Por tanto, el segundo coche recorre x kilómetros en un tiempo t - 1/2 y a una velocidad de 80 Km/h, es decir: x = 80 (t - 1/2)
Tenemos el siguiente sistema a resolver:
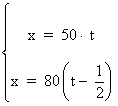
Lo resolvemos mediante el método de igualación.
50 · t = 80(t - (1/2)) ⇔ 50t = 80t - 40 ⇔ 40 = 80t - 50t ⇔ 40 = 30t ⇔ t = 1,33 h
0,3 · 60 = 19,9 min
El segundo coche tardará: 1 h 20 min
Si t = 1,3 h ⇒ x = 50t = 66,6 km
Ambos coches recorrerán: 66,6 km


 INICIO
INICIO