Ejercicios resueltos de ecuaciones de segundo grado
- 1. Completas
- 2. Incompletas
- 3. Ecuaciones
- 4. Racionales
- 5. Con literales
- 6. Propiedades
- 7. II
- 8. III
Ejercicios de ecuaciones completas de segundo grado:
1) x2 - 5x + 6 = 0
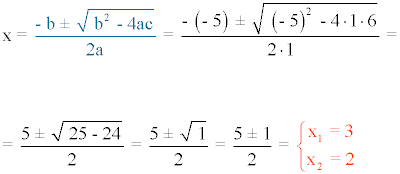
2) x2 + 10x + 25 = 0
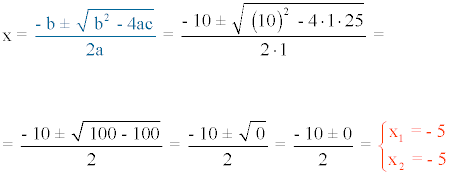
3) x2 + 2x + 2 = 0
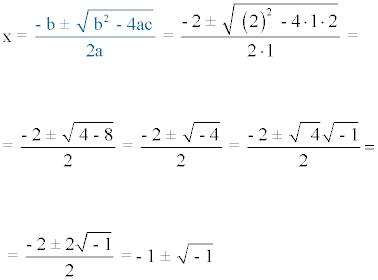
Por lo tanto, la ecuación no tiene soluciones reales.
4) 5x2 - 9x + 4 = 0
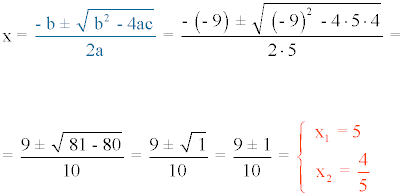
5) x2 + 3x + 1 = 0
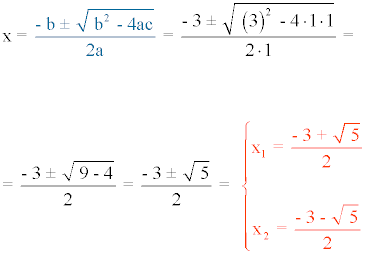
Ejercicios de ecuaciones incompletas de segundo grado:
A) ax2 + bx + c = 0 cuando c = 0
1) x2 + x = 0
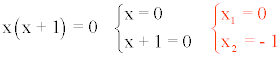
2) 4x2 + 12x - 9 = - 9
4x2 + 12x - 9 + 9 = 0
4x2 + 12x = 0
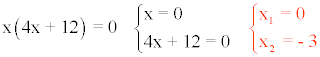
B) ax2 + bx + c = 0 cuando b = 0
3) x2 - 3 = 0
x2 = 3
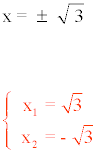
4) 4x2 - 25 = 0
4x2 = 25
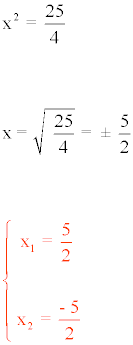
Resuelve las siguientes ecuaciones:
1) (x + 6) (x - 6) - 8 = 1 - 4x
x2 - 36 - 8 = 1 - 4x
x2 + 4x - 45 = 0
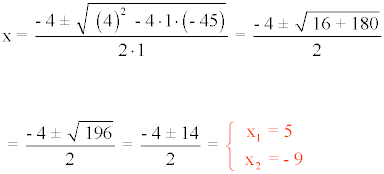
2) (2 - x) (5x + 1) - (3 + x) (x - 1) + 8x2 - 15x + 3 = 0
10x + 2 - 5x2 - x - 3x + 3 - x2 + x + 8x2 - 15x + 3 = 0
2x2 - 8x + 8 = 0
x2 - 4x + 4 = 0
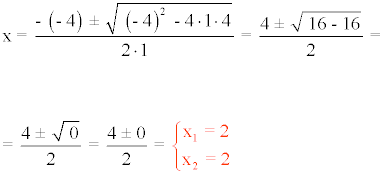
3) (x + 2) (x - 3) - x(2x + 1) + 6x = 0
x2 - 3x + 2x - 6 - 2x2 - x + 6x = 0
- x2 + 4x - 6 = 0
x2 - 4x + 6 = 0
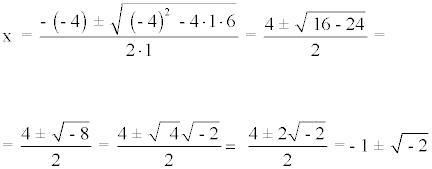
Por lo tanto, la ecuación no tiene soluciones reales.
4) x(x - 1)(x + 1) = 8[(x - 1) + x + (x + 1)]
x (x - 1)(x + 1) = 8 [ x - 1 + x + x + 1 ] ⇔ x (x2 - 1) = 8 · (3x) ⇔ x (x2 - 1) - 24x = 0 ⇔ x ( x2 - 25) = 0
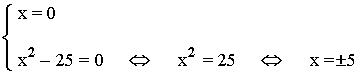
5) (18 - x)2 = (16 - x)2 + (9 - x)2
(18 - x)2 = (16 - x)2 + (9 - x)2 ⇔ 324 - 36x + x2 = 256 - 32x + x2 + 81 - 18x + x2 ⇔ x2 - 14x + 13 = 0
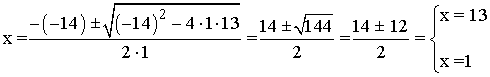
6) (x + 2)3 - x3 = 56
(x + 2)3 - x3 = 56 ⇒ (x3 + 6x2 + 12x + 8) - x3 = 56 ⇒ 6x2 + 12x + 8 = 56
6x2 + 12x - 48 = 0 ⇒ x2 + 2x - 8 = 0
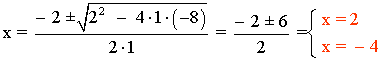
Ejercicios de ecuaciones racionales de segundo grado:
![]()
m.c.m. (3, x) = 3x
Para hacerlo de forma rápida dividimos el m.c.m. entre el denominador
y multiplicamos por el numerador en cada término.
3x2 + 3 = 10x
3x2 - 10x + 3 = 0
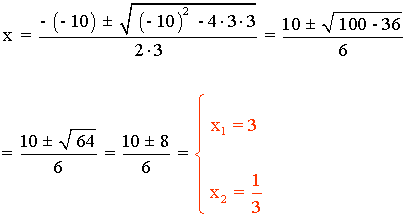
![]()
m.c.m. (x - 1, x + 2, x + 1) = (x - 1) (x + 2) (x + 1)
Para hacerlo de forma rápida dividimos el m.c.m. entre el denominador
y multiplicamos por el numerador en cada término.
6(x + 2)(x + 1) - 10(x - 1)(x + 1) = 4(x - 1)(x + 2)
6x2 + 18x + 12 - 10x2 + 10 = 4x2 + 4x - 8
- 8x2 + 14x + 30 = 0
4x2 - 7x - 15 = 0
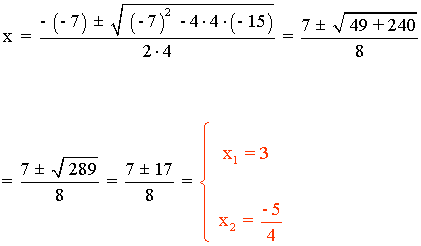
Ejercicios de ecuaciones de segundo grado con literales:
En estas ecuaciones las incógnitas se representan con las letras x , y , z.
Mientras que las letras a , b , c , m , n se utilizan como constantes.
1) x2 - 7ax + 12a2 = 0
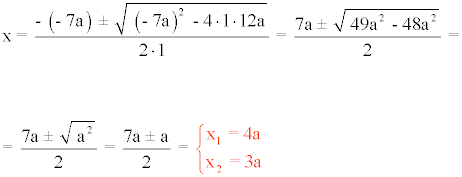
2) x2 - (a + b)x + ab = 0
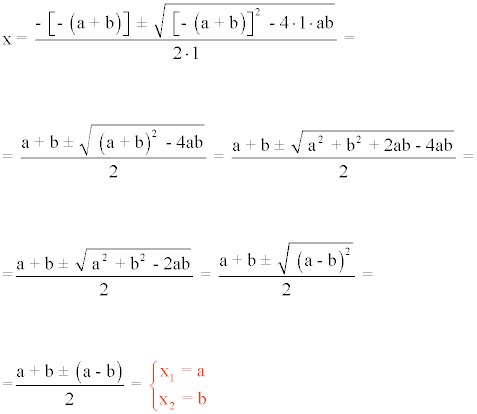
![]()
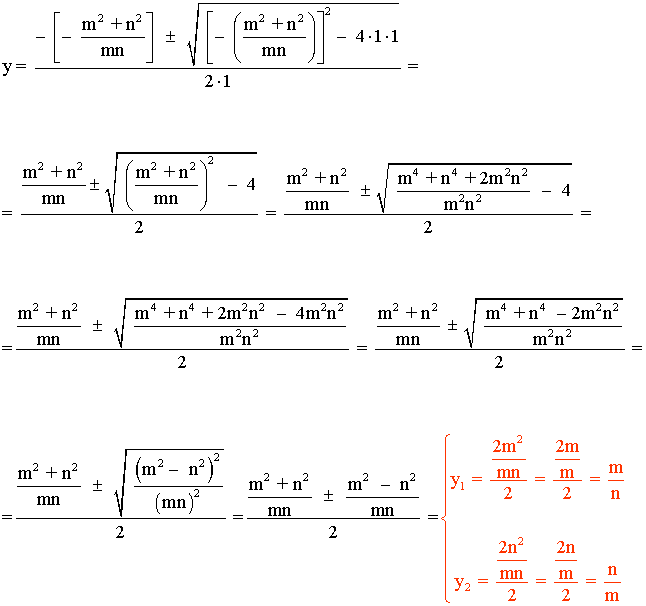
![]()
m.c.m. (b, a + b, x) = b (a+b) x
Para hacerlo de forma rápida dividimos el m.c.m. entre el denominador
y multiplicamos por el numerador en cada término.
x2 + ab = (a + b)x
x2 - (a + b)x + ab = 0
Esta ecuación es la misma del apartado 2)
Es decir, x1 = a y x2 = b
Propiedades de ecuaciones de segundo grado:
1) Calcula m para que x2 + mx + 25 = 0 tenga una solución.
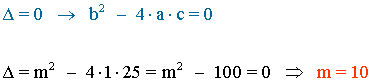
2) Calcula n para que x2 - 4x + n = 0 no tenga soluciones.
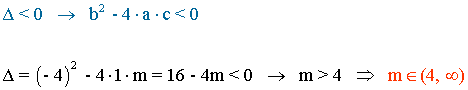
3) Calcula m para que mx2 + 8x + 5 = 0 tenga dos soluciones.
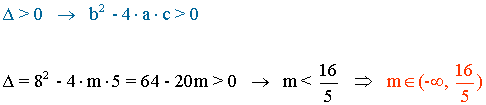
4) En las siguientes ecuaciones hallar la suma y producto de las raíces:
ax2 + bx + c = 0
![]()
![]()
![]()
a) x2 + 10x + 9 = 0
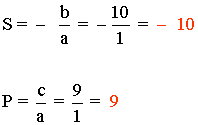
b) x2 - 8x + 7 = 0
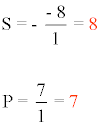
5) Forma las ecuaciones de segundo grado que tengan por raíces:
a) x1 = 3 y x2 = 4
S = 3 + 4 = 7
P = 3 · 4 = 12
Por lo tanto la ecuación es:
x2 - 7x + 12 = 0
También podemos encontrar la ecuación de segundo grado factorizando:
(x - 3) (x - 4) = x2 - 7x + 12 = 0
b) x1 = - 1 y x2 = 5
S = - 1 + 5 = 4
P = (- 1) · 5 = - 5
Por lo tanto la ecuación es:
x2 - 4x - 5 = 0
También podemos encontrar la ecuación de segundo grado factorizando:
(x + 1) (x - 5) = x2 - 4x - 5 = 0
c) x1 = - 20 y x2 = - 2
S = - 20 - 2 = - 22
P = (- 20) · (- 2) = 40
Por lo tanto la ecuación es:
x2 + 22x + 40 = 0
También podemos encontrar la ecuación de segundo grado factorizando:
(x + 20) (x + 2) = x2 + 22x + 40 = 0
d) x1 = 5 y x2 = 1/5
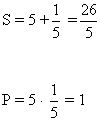
Por lo tanto la ecuación es:
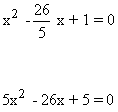
También podemos encontrar la ecuación de segundo grado factorizando:
![]()
Propiedades de ecuaciones de segundo grado:
1) Hallar dos números que tengan:
a) Por suma - 3 y por producto - 28.
Los números buscados son las ráices de la ecuación:
x2 + 3x - 28 = 0
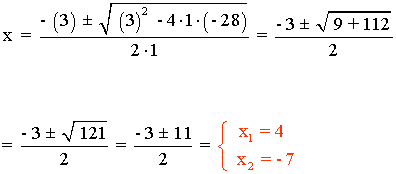
b) Por suma - 8 y por producto 12.
Los números buscados son las ráices de la ecuación:
x2 + 8x + 12 = 0
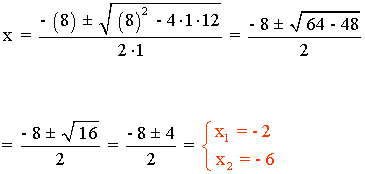
2) En la ecuación x2 + Kx - 28 = 0 , hallar el valor
de K sabiendo que una de las raíces es - 7.
K = x1 + x2 y - 28 = x1·x2
Por lo tanto: - 28 = (- 7)·x2
De aquí obtenemos que, x2 = 4
Y por lo tanto, K = - 7 + 4 = -3
Luego la solución es: K = - 3
3) En la ecuación K(x2 - 5x + 1) - 6(x+2) + 4(K - x) - 65 = 0 ,
hallar el valor de K sabiendo que una de sus raíces es x = - 2.
Como x = 2 es una raíz, satisface la ecuación anterior.
K·[(- 2)2 - 5·(- 2) + 1] - 6·[(- 2) + 2] + 4·[K - (- 2)] - 65 = 0
15K + 4(K + 2) - 65 = 0
15K + 4K + 8 - 65 = 0
19K = 57
Por lo tanto, K = 3
Propiedades de ecuaciones de segundo grado:
1) Hallar m para que las raíces de x2 - 6mx + 9m2 = 0 sean iguales.
Para que las raíces sean iguales el discriminante de la ecuación debe ser igual a 0.
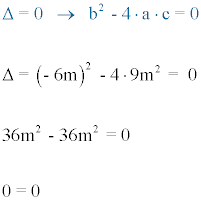
Por lo tanto cualquier valor real de m lo cumple.
2) Hallar m para que las raíces de x2 - (m + 1)x + 2m + 3 = 0 difieran en 4 unidades.
S = x1 + x2 = x1 + (x1 + 4)
2·x1 + 4 = m + 1
P = x1 · x2 = x1·(x1 + 4)
x12 + 4x1 = 2m + 3
Por lo tanto tenemos el siguiente sistema:
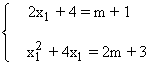
De la primera ecuación obtenemos que:
![]()
Sustituyendo en la segunda ecuación obtenemos:
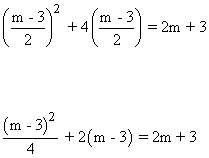
m.c.m. (1, 4) = 4
Dividiendo el m.c.m. entre el denominador y multiplicando
por el numerador en cada término llegamos a:
(m - 3)2 + 8(m - 3) = 4(2m + 3)
m2 - 6m + 9 + 8m - 24 = 8m + 12
m2 - 6m - 27 = 0
A continuación resolvemos la ecuación de segundo grado:
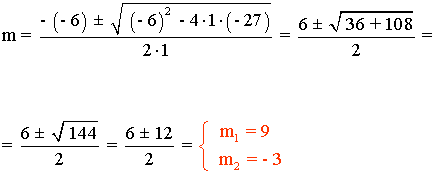
También podemos encontrar la solución factorizando:
(x - x1) [x - (x1 + 4)] = x2 - (m + 1)x + 2m + 3
(x - x1) (x - x1 - 4) = x2 - (m + 1)x + 2m + 3
x2 - x·x1 - 4x - x·x1 + x12 + 4·x1 = x2 - (m + 1)x + 2m + 3
x2 - (2x1 + 4)x + (x12 + 4·x1) = x2 - (m + 1)x + 2m + 3
Igualando los coeficientes de cada término de la ecuación de segundo grado obtenemos:
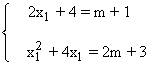
Es decir, el mismo sistema de ecuaciones que con el método anterior.
3) Calcula m para que la ecuación x2 - 8mx + m + 1 = 0 tenga una raíz el triple de la otra.
Si una raíz es el triple de la otra, entonces: x1 = x y x2 = 3x
S = x + 3x = 8m
P = x · 3x = m + 1
Por lo tanto tenemos el siguiente sistema de ecuaciones:
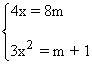
De la primera ecuación obtenemos que:
x = 2m
Si sustituimos el valor de x en la segunda ecuación resulta:
3 · (2m)2 = m + 1
12m2 - m - 1 = 0
A continuación resolvemos la ecuación de segundo grado para resolver el problema.
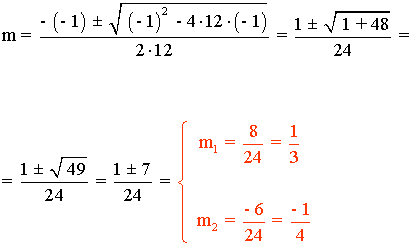


 INICIO
INICIO