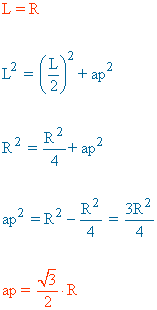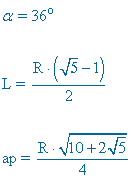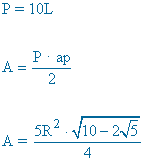Ejercicios resueltos de polígonos
| Polígono | Lados | Ángulo central (β) | Ángulo interior (α) | Suma de ángulos interiores (Si ) | Número de diagonales (ND ) |
|---|---|---|---|---|---|
| Pentágono | 5 | ||||
| Hexágono | 6 | ||||
| Octógono | 8 | ||||
| Dodecágono | 12 | ||||
| n lados | n |
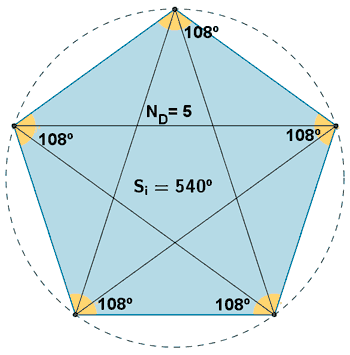
Polígonos regulares de n lados inscritos en una circunferencia
| Nombre | Dibujo | Lado y apotema | Perímetro y área |
|---|---|---|---|
| Triángulo | 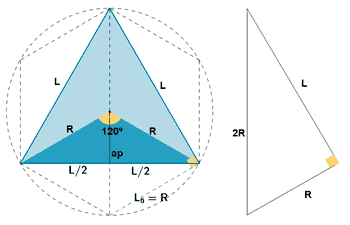 |
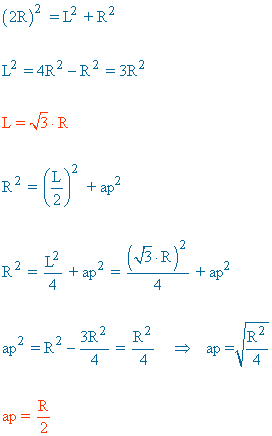 |
ap = apotema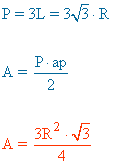 |
| Cuadrado | 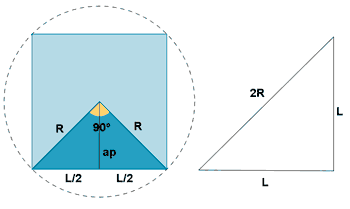 |
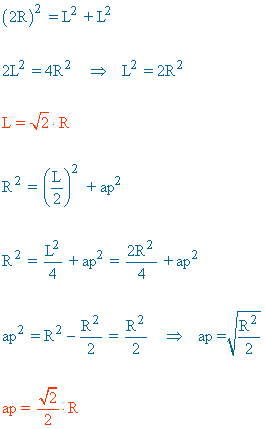 |
ap = apotema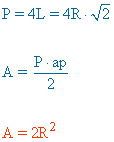 |
| Hexágono | 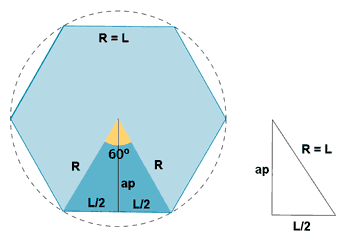 |
|
ap = apotema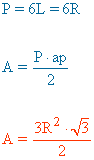 |
| Nombre | Dibujo | Lado y apotema | Perímetro y área |
|---|---|---|---|
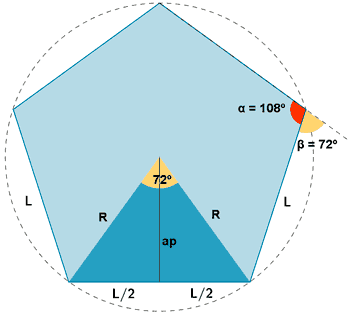
| Pentágono | 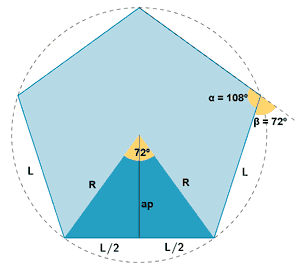 |
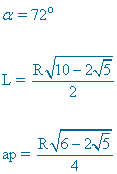 |
ap = apotema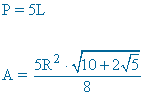 |
| Octógono | 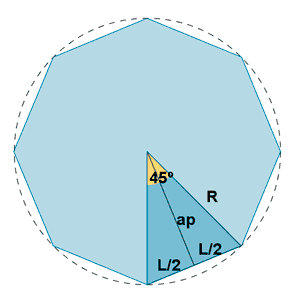 |
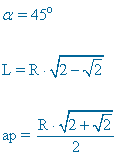 |
ap = apotema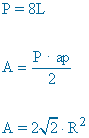 |
| Decágono | 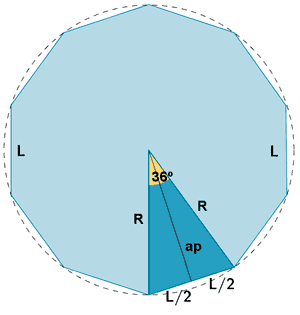 |
|
ap = apotema
|
Polígonos regulares de n lados circunscritos en una circunferencia
| Nombre | Dibujo | Lado y apotema | Perímetro y área |
|---|---|---|---|
| Triángulo | 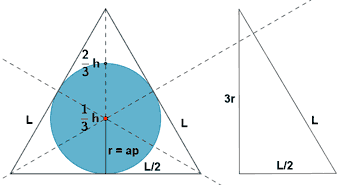 |
ap = apotema = r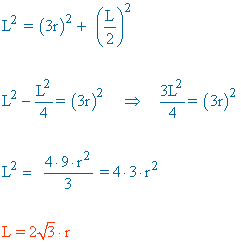 |
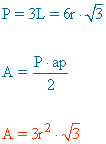 |
| Cuadrado | 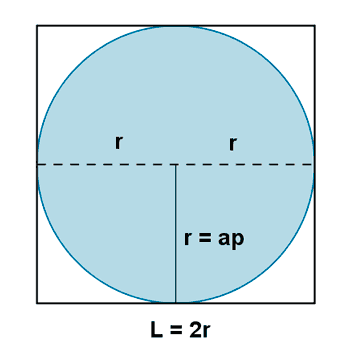 |
ap = apotema = r |
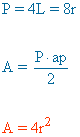 |
| Hexágono | 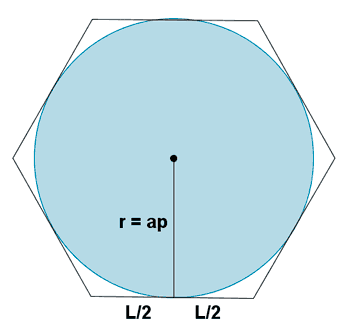 |
ap = apotema = r |
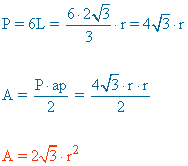 |
Polígonos irregulares
| Nombre | Dibujo | Perímetro | Área |
|---|---|---|---|
| Polígono irregular | 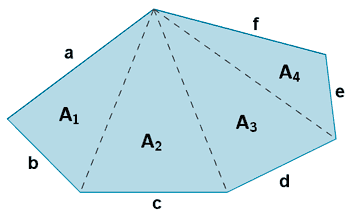 |
P = a+b+c+d+e+f | A = A1+A2+A3+A4 |
1 ) Hallar la fórmula del área de un triángulo equilátero en función del lado a y su altura.
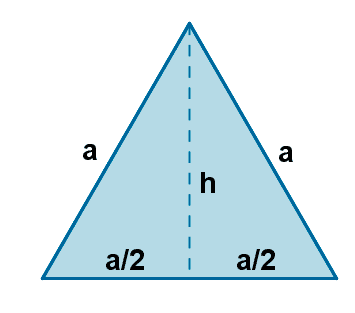
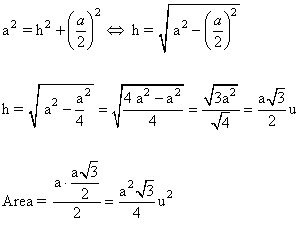
2 ) Calcular el lado y la apotema de un triángulo equilatero circunscrito en una circunferencia de 6 cm de radio.
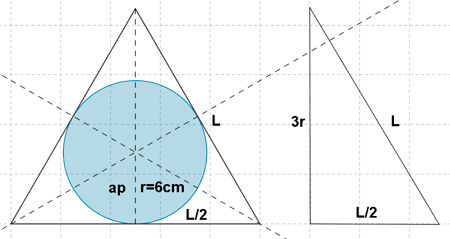
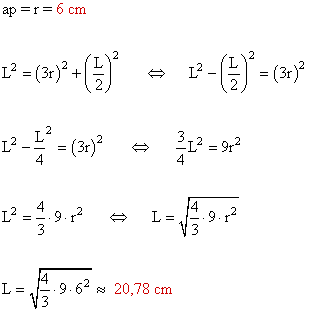
3 ) Hallar el área comprendida entre las circunferencias circunscrita e inscrita a un triángulo equilátero de 18√3 cm de perímetro.
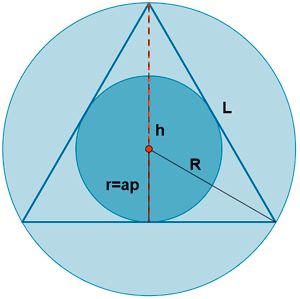
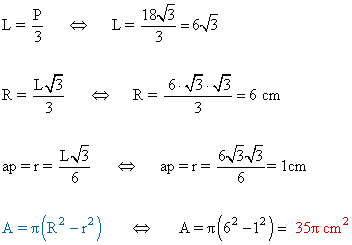
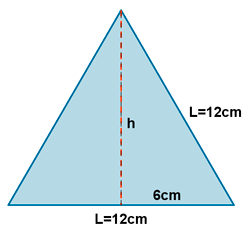
4 ) En un triángulo equilatero cuyo lado mide 12 cm, calcular:
a) La longitud de sus medianas.
b) El radio de la circunferencia inscrita.
c) El radio de la circunferencia circunscrita.
En los triángulos equiláteros, las medianas, alturas, mediatrices y bisectrices coinciden.
a )
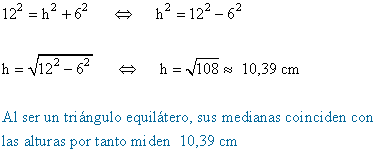
b )
Sabemos que el baricentro de un triángulo está a 2/3 h de distancia del vértice y a 1/3 h de distancia del lado ( Como el triángulo es equilátero, las medianas coinciden con las alturas).
Como sabemos que el triángulo es equilátero conocemos que el incentro coincide con el baricentro, por tanto el radio de la circunferencia inscrita es 1/3 h.
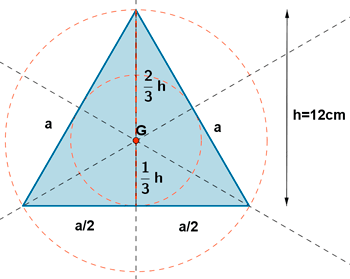
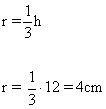
c )
Con el mismo razonamiento del apartado b y como baricentro coincide con el circuncentro y estamos a su vez en un triángulo rectángulo el radio de la circunferencia circunscrita vale 2/3 h.

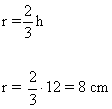
5 ) Calcula el lado y la apotema de un cuadrado circunscrito en una circunferencia de 3 cm de radio.
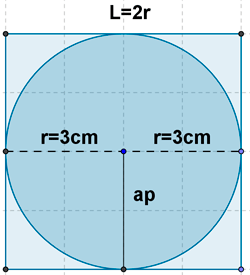
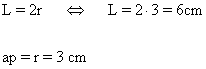
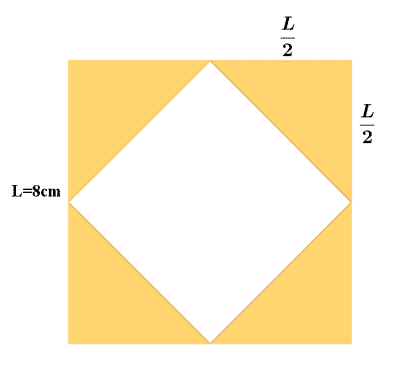
6 ) Calcular el perímetro y el área de las siguientes figuras coloreadas.
a )
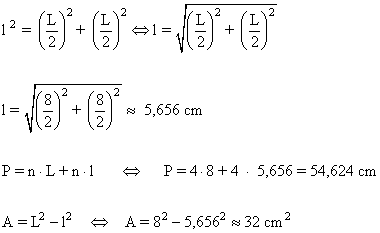
b )
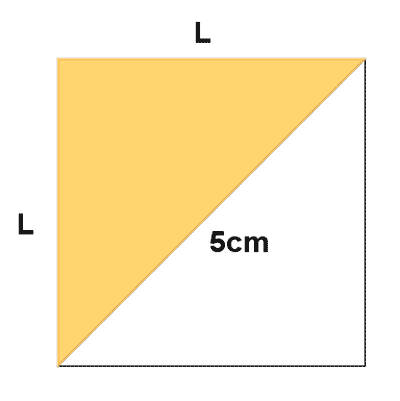
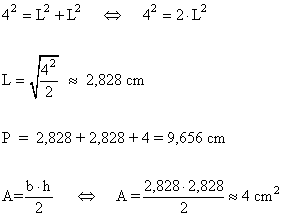
7 ) Calcular el área coloreada de las siguientes figuras.
a )
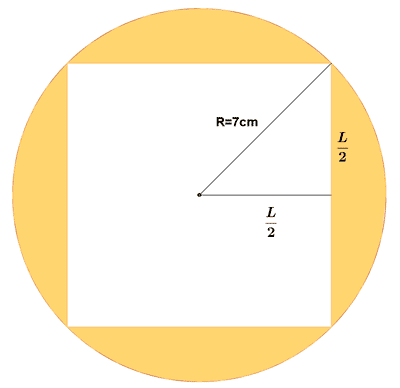
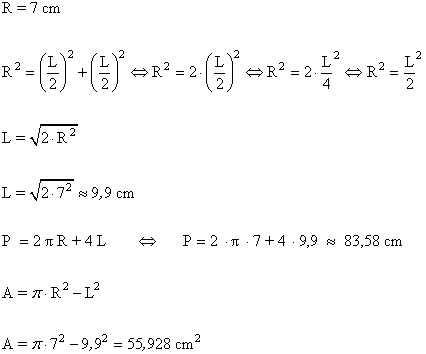
b )
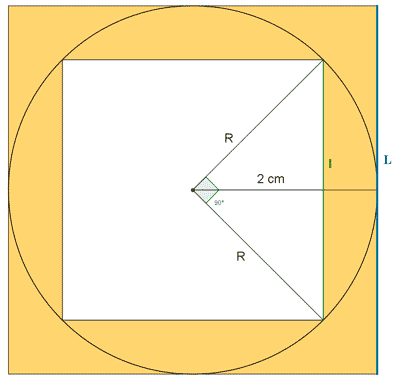
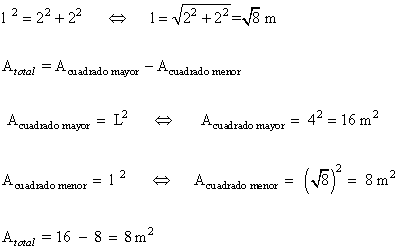
8 ) Calcula el lado y la apotema de un cuadrado inscrito en una circunferencia de 5 cm de radio.

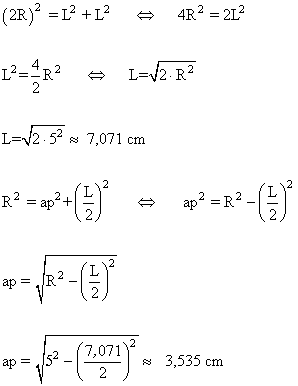
9 ) Calcular el lado y la apotema de un triángulo equilatero inscrito en una circunferencia de 8 cm de radio.
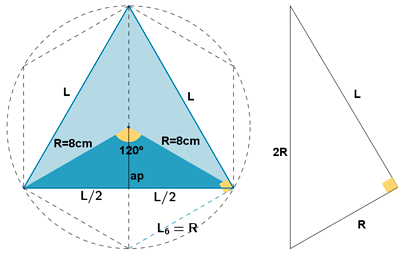
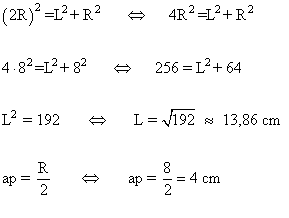
10 ) Calcula la apotema de un hexagono inscrito en una circunferencia de 7 cm de radio.

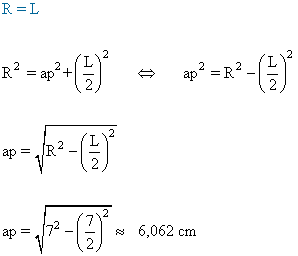
11 ) Calcular el perímetro y el área de las siguientes figuras.
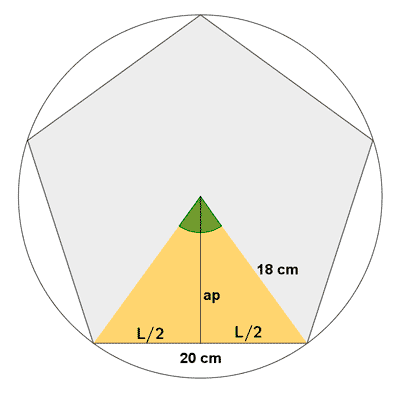
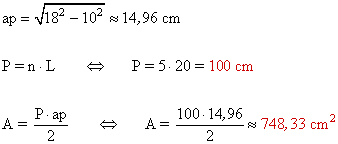
12 ) Calcular el perímetro y el área de las siguientes figuras.
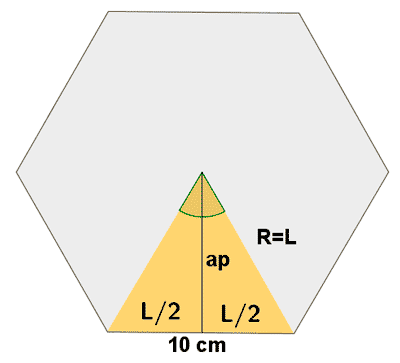
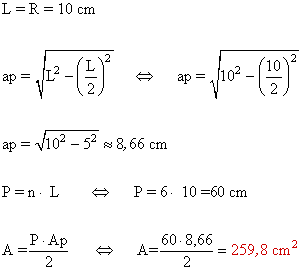
13 ) Calcular el perímetro y el área de las siguientes figuras.
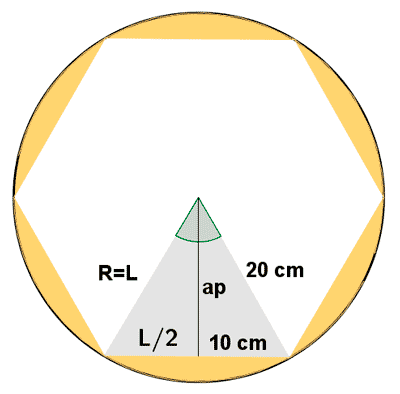
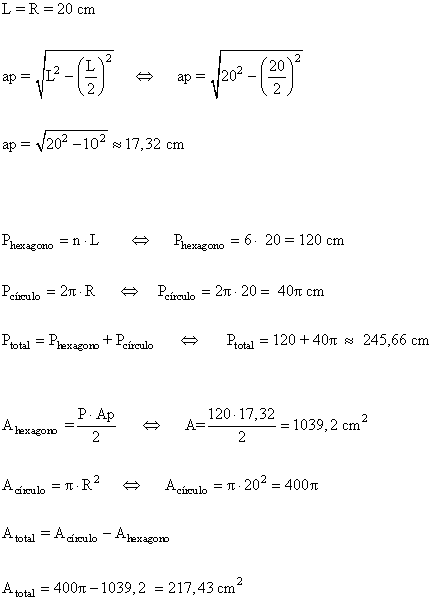
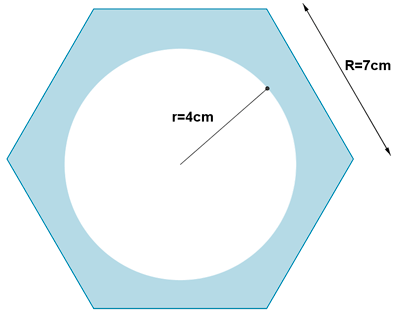
14 ) Calcula el área y el perímetro de la siguiente figura.
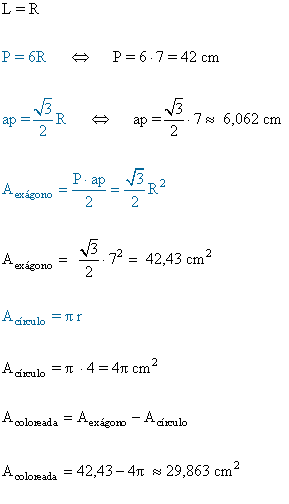
15 ) En un triángulo isósceles inscrito en una circunferencia conocemos su diámetro (D = 5 m) y la altura del triángulo (h = 4 m). Halla cuanto mide la base del triángulo.
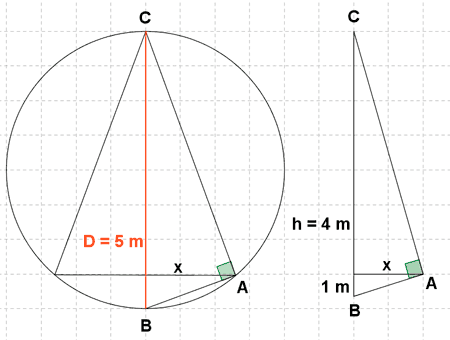
El triángulo ABC es rectángulo en A porque un lado es un diámetro y el lado opuesto está inscrito en la circunferencia.
Aplicando el teorema de la altura tenemos que:
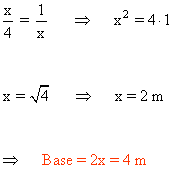
16 ) Se tiene un rectángulo inscrito en una circunferencia. Sabiendo que el diámetro de la circunferencia es de 6 metros y que la altura del rectángulo es h = 5 m, halla cuánto mide la base del rectángulo.
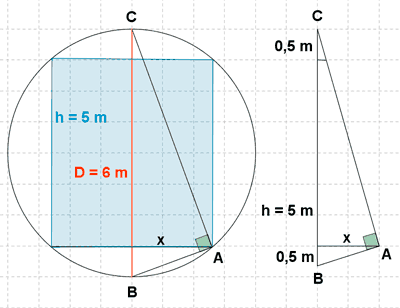
El triángulo ABC es rectángulo en A porque un lado es un diámetro y el lado opuesto está inscrito en la circunferencia. Aplicando el teorema de la altura tenemos que:
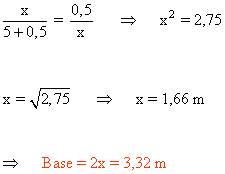


 INICIO
INICIO