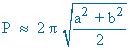Ejercicios resueltos de figuras circulares
Perímetro y área de figuras circulares
| Nombre | Dibujo | Perímetro | Área |
|---|---|---|---|
| Círculo | 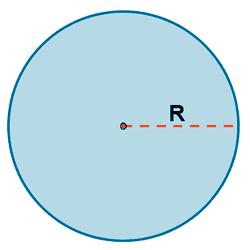 |
L = 2π·R | A = π·R2 |
| Sector circular |
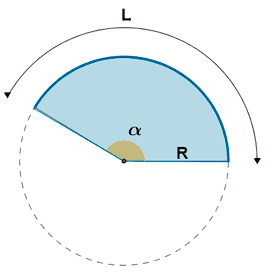 |
P = 2R + L α en grados: α en radianes: L = R α |
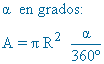 |
| Triángulo circular | 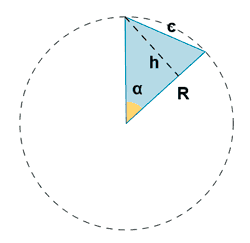 |
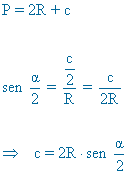 |
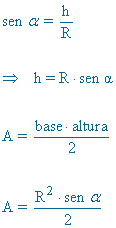 |
| Segmento circular | 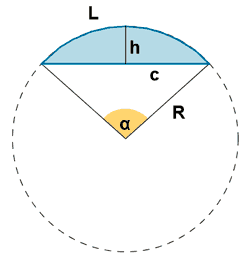 |
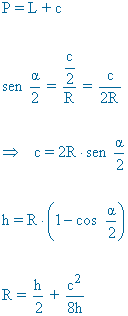 |
Área segmento circular = area sector circular - área triángulo circular 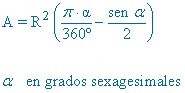 |
| Corona circular |
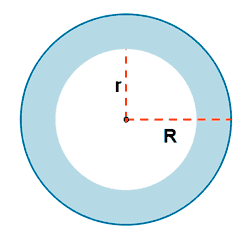 |
P = 2π·R + 2π·r · P = 2p·(R + r) |
A = π·(R2 - r2) |
| Trapecio circular | 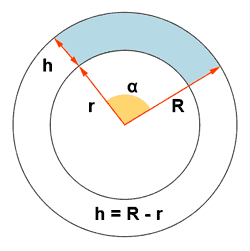 |
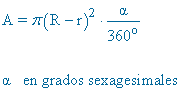 |
|
| Elipse | 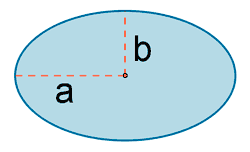 |
Valor aproximado:
|
A = π·a·b |
| Segmento de parábola | 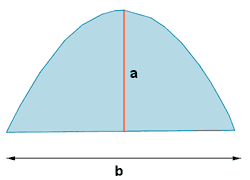 |
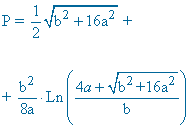 |
1-a ) Una cuerda está a 8 cm de distancia del centro de una circunferencia de 18 cm de radio. Halla la longitud de la cuerda.
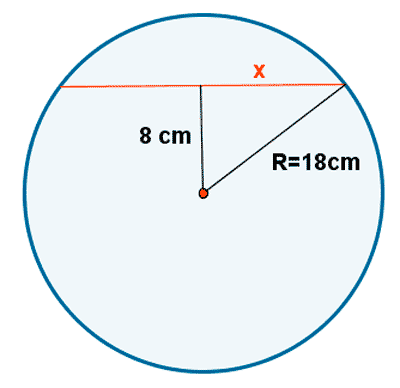
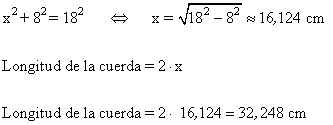
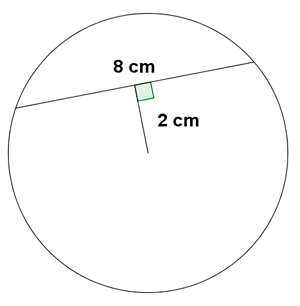
1-b ) Calcular el radio de una circunferencia que tiene una cuerda de 8 cm de longitud. La distancia desde la cuerda hasta el centro de la circunferencia es de 2 cm. ¿Cúal será la longitud de una cuerda cuya distancia al centro es de 2,5 cm?
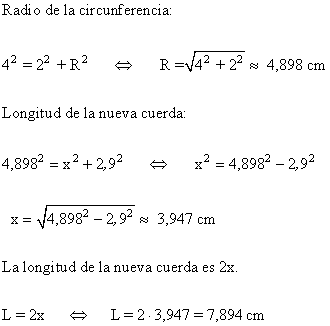
2) Se va a perforar un túnel por el que circulará un vagón de 3m de ancho y 2m de alto. ¿Qué diámetro mínimo tendrá la sección del túnel?.
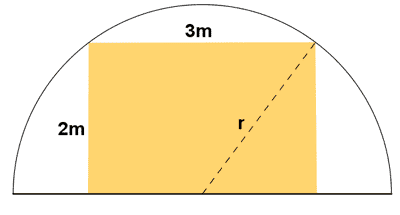
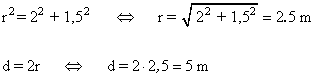
3 ) En un círculo de 40 cm de diametro trazamos una cuerda que dista del centro una distancia de 6 cm. Hallar el área del cuadrilatero que se forma al juntar los extremos de la cuerda con los del diametro paralelos a ella.

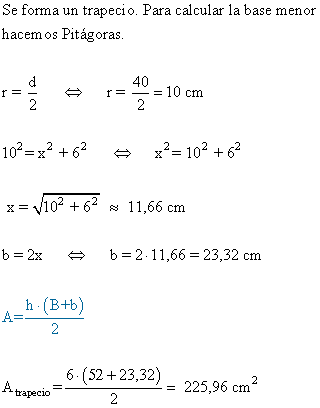
4-a ) Desde cierto punto A que dista 35 cm del centro de una circunferencia de radio 25 cm, se traza una tangente. Calcular la distancia desde A hasta el punto de tangencia
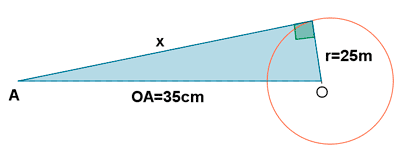
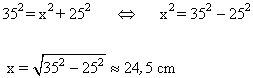
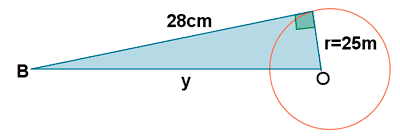
4-b ) Realizamos otra tangente desde otro punto B y al medir la distancia de P al punto de tangencia obtenemos 28 cm. ¿Cúal es la distancia de B al centro de la circunferencia?
![]()
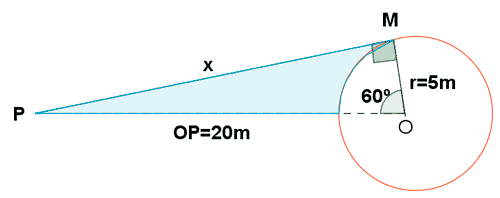
5 ) Calcular:
a) La longitud de x
b) El área de la parte coloreada.
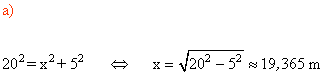
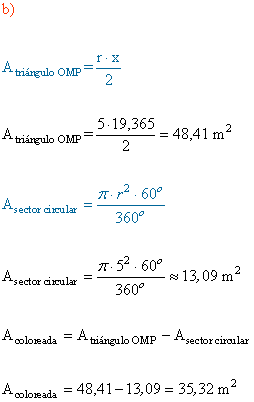
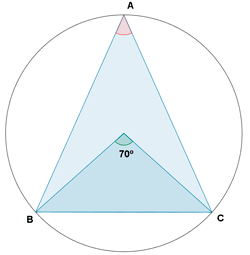
6-a ) Tenemos un triángulo ABC el cual es isósceles donde AB=BC. Calcular cuanto miden los ángulos de ese triángulo.
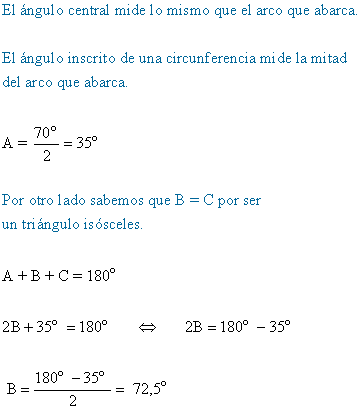
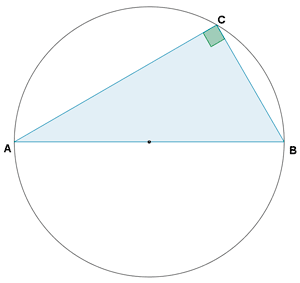
6-b ) Al dibujar un triángulo ABC inscrito en una circunferencia, de modo que sus vértices A y B sean extremos de un diámetro y el arco BC sea la sexta parte de la circunferencia. ¿Cúanto miden los ángulos de ese triángulo?

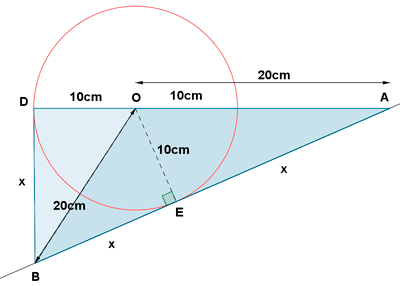
7 ) De la siguiente figura se conoce:
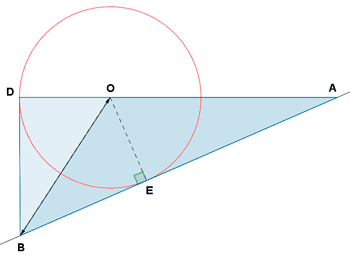
a ) Radio: 10cm
b ) OA = OB = 20 cm
c ) AB es tangente a la circunferencia en E.
d ) BD es tangente a la circunferencia en D.
Calcula el perímetro y el área de los triángulos ABQ y AOB.
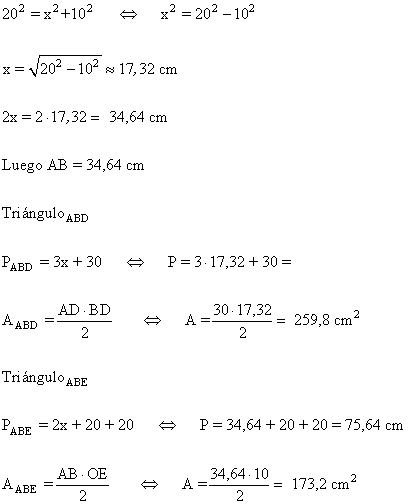
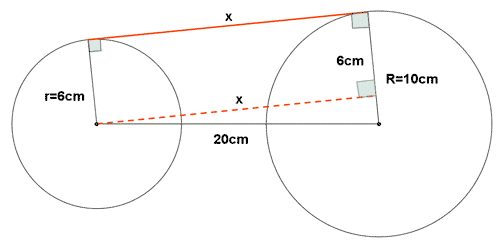
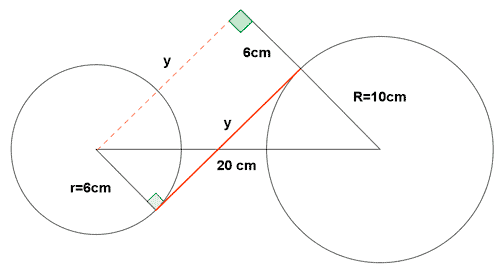
8 ) Los radios de dos circunfderencias son r= 6 cm y R = 10 cm. La distancia entre sus centros es de 20 m. Halla las longitudes de los segmentos de tangente común externa e interna.
![]()
![]()
9 ) El segmento de la tangente común exterior de dos circunferencias mide 20 cm y sus radios son r= 8 cm y R=12cm. Averigua si las circunferencias son secantes o exteriores.
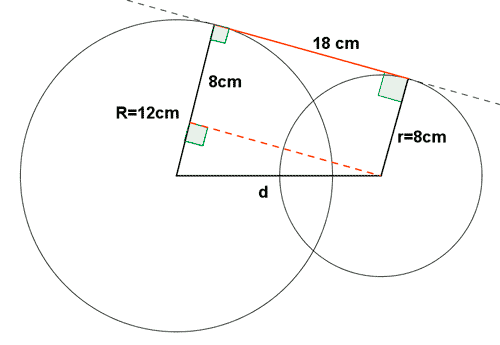
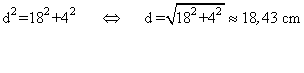
La suma de R + r > d
12 + 8 = 20 cm > 18,43 cm
Por tanto, las circunferencias son secantes.
10 ) Dibuja dos circunferencias O y O' tangentes exteriormente y de radios 10 cm y 28 cm, respectivamente. Traza una tangente común y llama P y Q a los puntos de tangencia.
a ) ¿Cómo son entre sí los radios OP y O'Q? ¿ Qué cuadrilatero es la figura OO'PQ?
b? Determina el perímetro y el área de cuadrilátero OO'PQ
a )
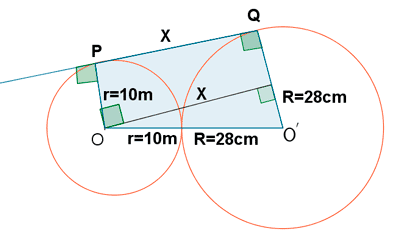
Los radios OP y O'Q son paralelos entre si. La figura OO'PQ es un trapecio rectángulo.
b )
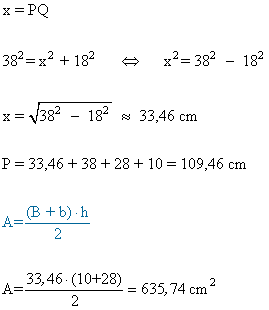
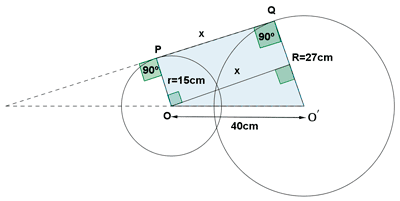
11 ) Dibujar dos circunferencias secantes de radio 15 cm y 27 cm. Traza una tangente común y llamar P y Q a los puntos de tangencia.
Calcula el perímetro y el área del cuadrilatero OO'PQ sabiendo que la distancia entre los centros OO' es 40 cm
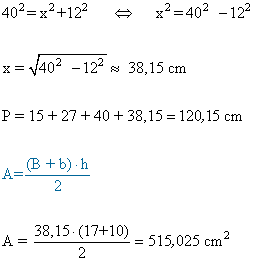
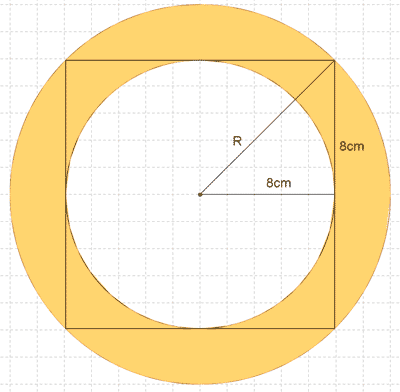
12 ) Calcular el perímetro y el área de las siguientes figuras coloreadas.
a )
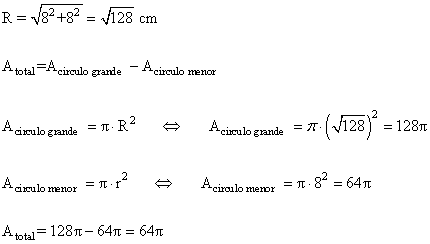
b )
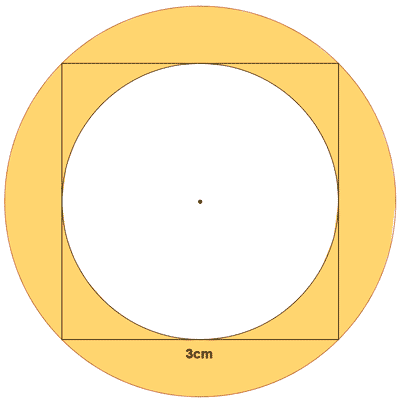
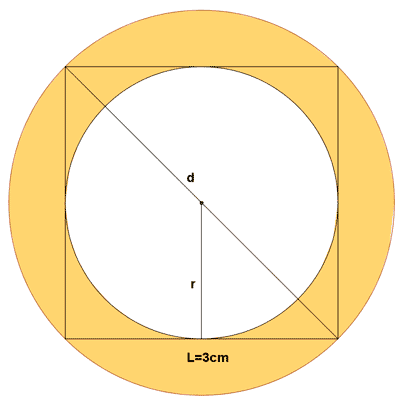
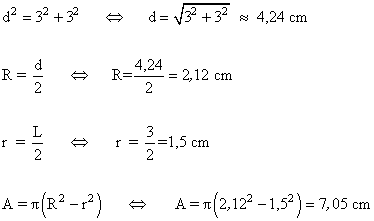
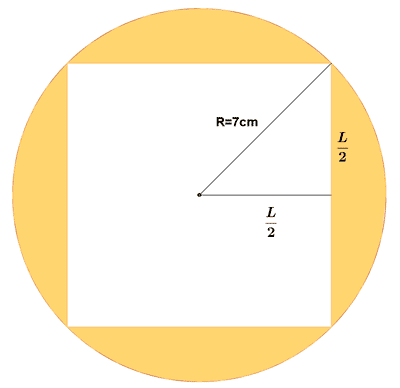
13 ) Calcular el área coloreada de las siguientes figuras.
a)
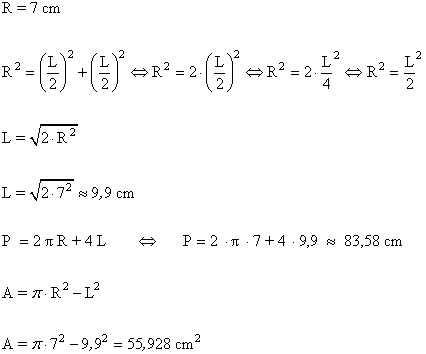
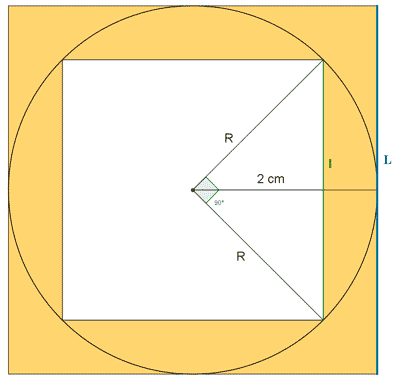
b )
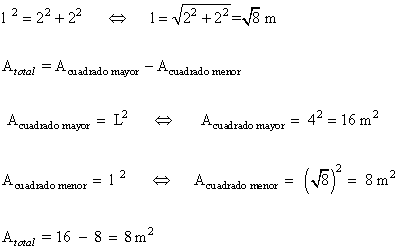
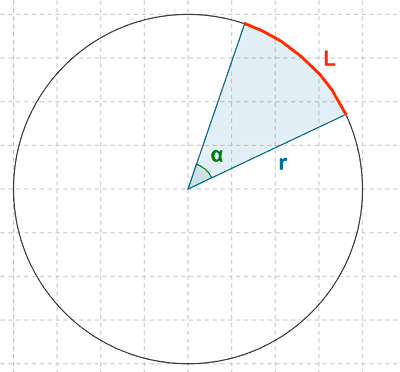
14 ) Hallar la medida en radianes de un ángulo central contenido por un arco de 35 cm en una circunferencia de radio 5 cm.
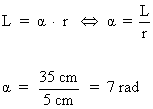
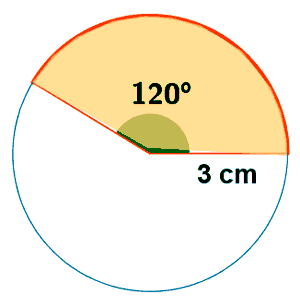
15 ) Determina el área de un sector circular que abarca un ángulo de 120º y tiene un radio de 3 cm.
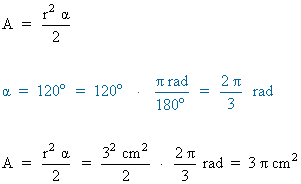
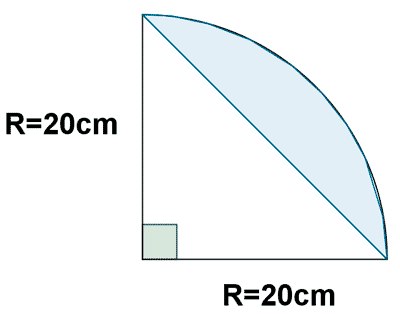
16 ) Calcula el área de un segmento circular de 90º de amplitud en un círculo de 20 cm de radio.
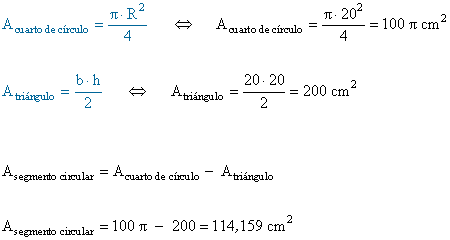


 INICIO
INICIO