Ejercicios resueltos de poliedros irregulares
Área y volumen de los poliedros irregulares
(cuerpos geométricos limitados por polígonos)
| Dibujo | Área | Volumen | |
|---|---|---|---|
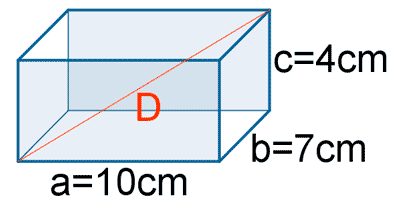
| Ortoedro | 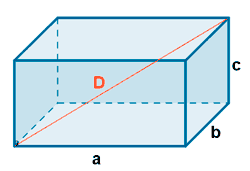 |
A t = 2·(a·b + a·c + b·c) |
V = a·b·c |
| Cuña | 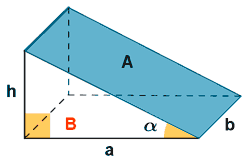 |
A = área cara superior AB = área base A = AB sec α |
|
| Prisma triangular | 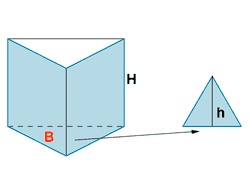 |
AL = PB·h AT = AL + 2·AB |
ap = apotema PB = perímetro de la base AL = área lateral AB = área base AT = área total |
| Prisma cuadrangular | 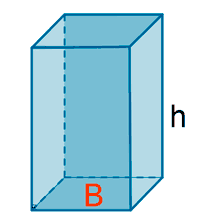 |
AL = PB·h
AT = AL + 2·AB |
|
| Prisma pengatonal | 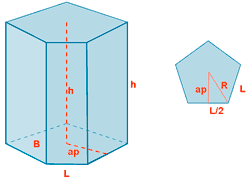 |
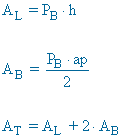 |
|
| Prisma hexagonal | 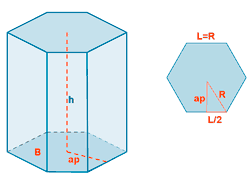 |
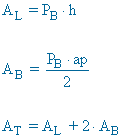 |
|
| Pirámide cuadrangular | 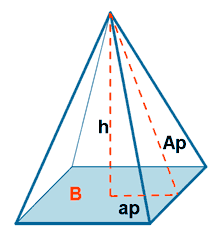 |
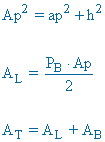 |
PB = perímetro base
|
| Pirámide pentagonal | 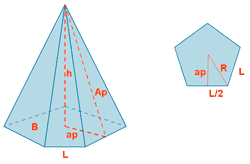 |
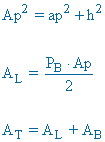 |
|
| Pirámide hexagonal | 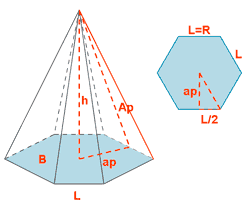 |
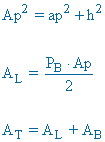 |
|
| Tronco de piramide cuadrangular | 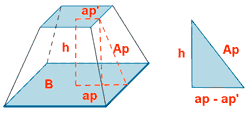 |
P = perímetro base mayor p = perímetro base menor 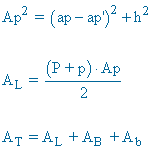 |
Ap = apotema tronco |
| Tronco de piramide hexagonal | 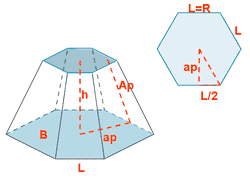 |
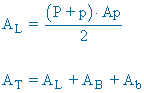 |
1 ) Calcula el área y el volumen de un ortoedro cuyas arisata miden 10 cm, 7cm y 4 cm.
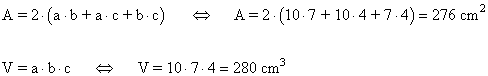
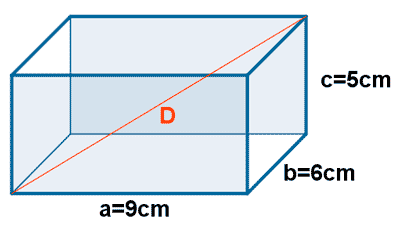
2 ) Calcula la diagonal del ortoedro cuyas aristas miden 9 cm, 6 cm y 5 cm.
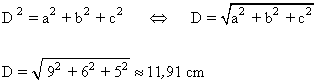
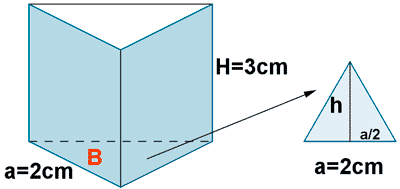
3 ) Calcula el área y el volumen de un prisma recto de altura 3 m y que tiene por base un triángulo equilatero de 2 m de arista.
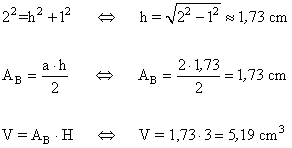
4 ) Calcula el área y el volumen de un prisma cuadrangular el el que su la arista de la base mide 4 dm y su altura es de 11 dm.
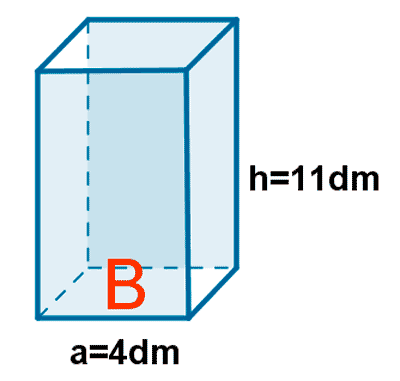
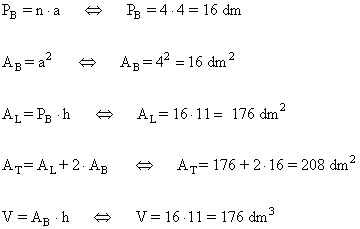
5 ) Calcula el área y el volumen de un prisma hexagonal en el que la arista de la base mide 14 m y su altura es de 27 m.
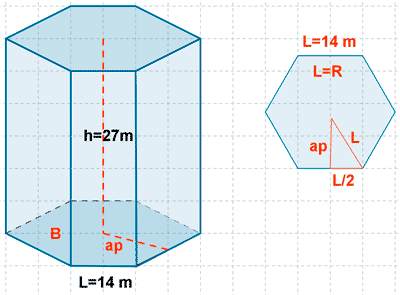
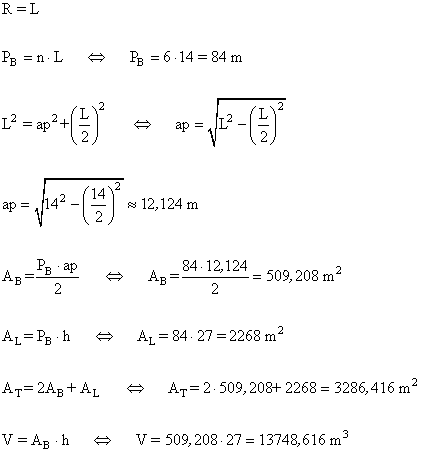
6 ) Calcular la altura de una piramide cuadrangular de apotema lateral 12 cm y la base tiene una arista de 10 cm.
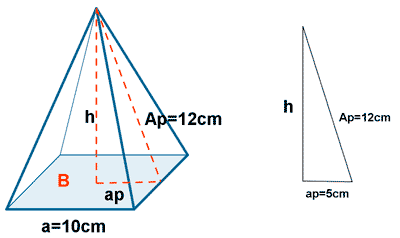
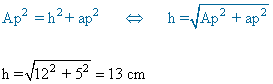
7 ) Calcula el área y el volumen de una pirámide cuadrangular cuya base tiene 4 cm de arista y una altura de 6 cm.
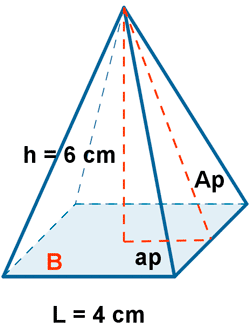
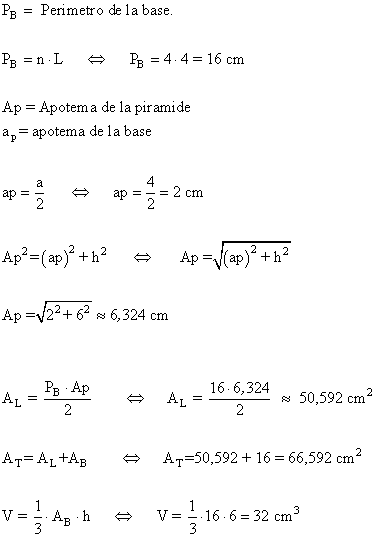
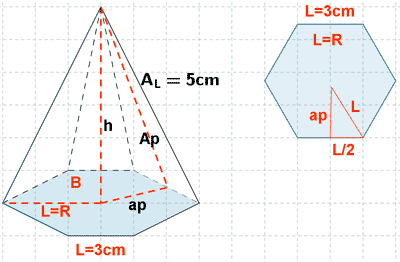
8 ) Hallar el área y el volumen de una piramide hexagonal en la que la arista de la base mide 3 cm y la arista lateral 5 cm.
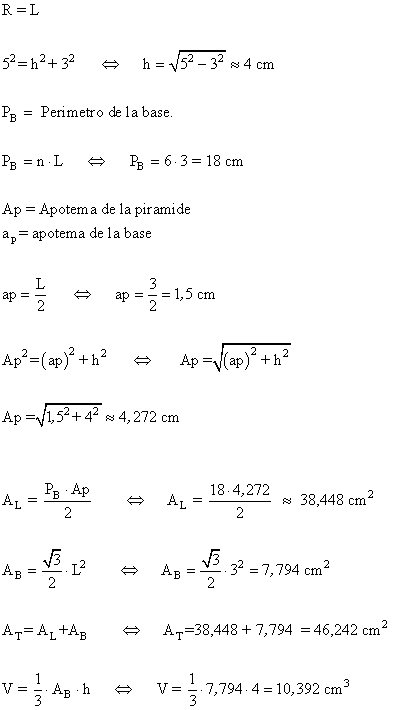
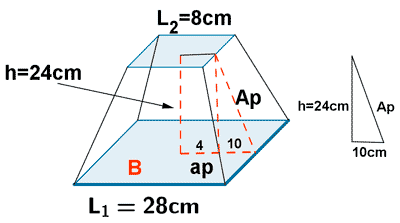
9 ) Haz el digujo y halla el área y el volumen de un tronco de pirámide cuadrada en el que la arista de la base mayor mide 28 cm, la arista de la base menor 8 cm y la altura 24 cm.
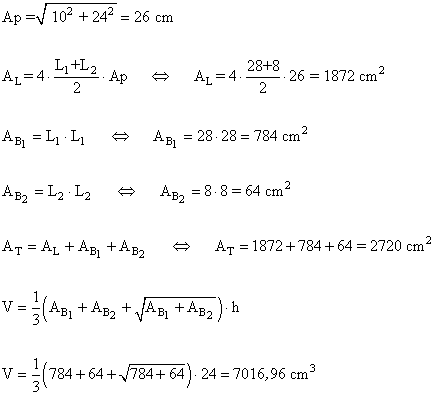
10) Calcula el volumen del tronco de pirámide de la figura.
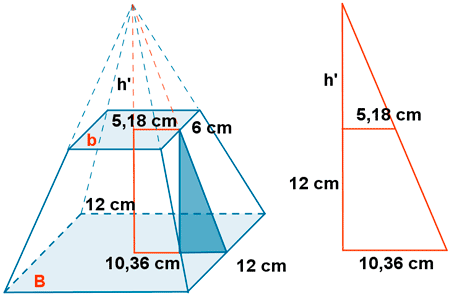

11 ) Calcular el volumen de la siguiente figura.
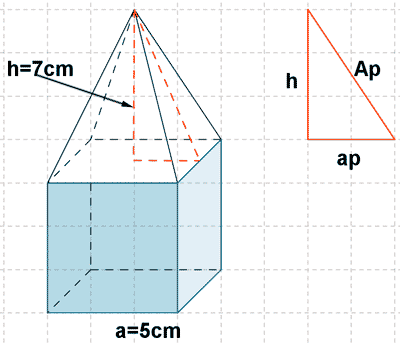
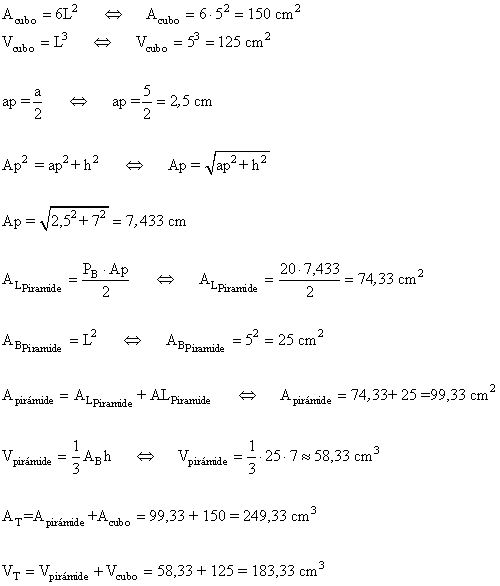


 INICIO
INICIO