Límite de una sucesión.
Representación gráfica de algunas sucesiones.
Ejemplo 1:
Si en la expresión ![]() sustituimos n por 1, 2, 3,..., 100, ..., 1000 ... Se obtienen los siguientes resultados:
sustituimos n por 1, 2, 3,..., 100, ..., 1000 ... Se obtienen los siguientes resultados:
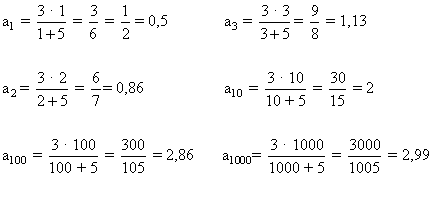
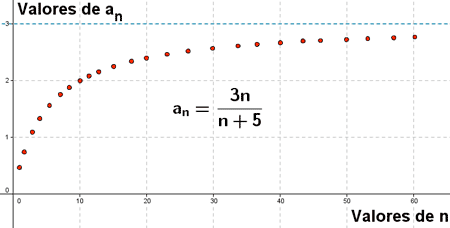
Los elementos de la sucesión se acercan cada vez más a 5, por tanto lo expresamos:
![]()
Ejemplo 2:
Si en la expresión 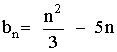 sustituimos n por 1, 2, 3,..., 100, ..., 1000 ... Se obtienen los siguientes resultados:
sustituimos n por 1, 2, 3,..., 100, ..., 1000 ... Se obtienen los siguientes resultados:
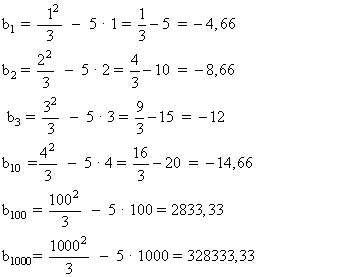
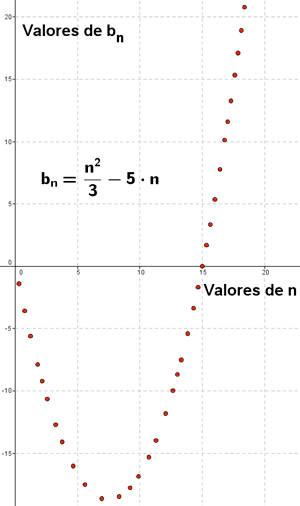
Los elementos de la sucesión, aunque al principio decrecen, después se hacen cada vez más grandes, por tanto lo expresamos:
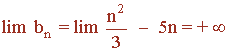
Ejemplo 3:
Si en la ![]() expresión sustituimos n por 1, 2, 3,..., 100, ..., 1000 ... Se obtienen los siguientes resultados:
expresión sustituimos n por 1, 2, 3,..., 100, ..., 1000 ... Se obtienen los siguientes resultados:
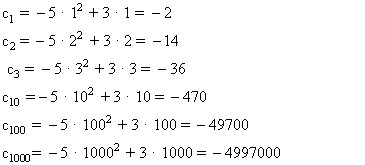
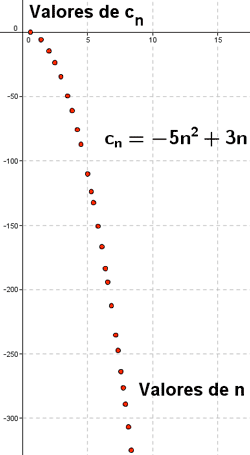
Los elementos de la sucesión se hacen cada vez más pequeños, por tanto lo expresamos:
![]()
Sucesiones que no tienen límite.
Ejemplo 4:
La sucesión ![]() :
:
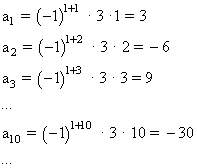
Esta sucesión no se acerca a ningún número ni tiende a +∞ porque los términos pares son negativos ni a -∞ porque los términos impares son positivos, por tanto no tiene límite. Se llaman sucesiones oscilantes.
Resumen de límite de sucesiones.
| Sucesión | Límite de la sucesión |
|---|---|
| Que la sucesión se acerque a un número L | |
| Que la sucesión crezca superando cualquier número | |
| Que decrezca por debajo de cualquier número | |
| Que oscile |
Sucesiones convergentes y divergentes.
Una sucesión se dice que es convergente cuando el límite de la sucesión es un número real.
Se dice que una sucesión es divergente cuando no tiene límite o tienden a infinito.
Ejemplo 5:
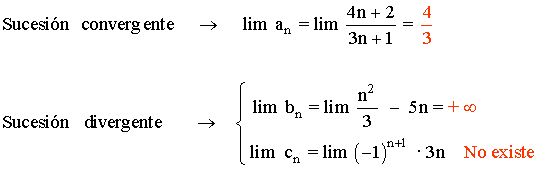
Propiedades de los límites de las sucesiones convergentes.
Ejemplos:
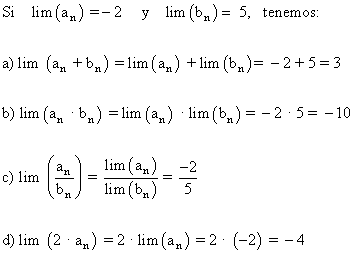
| Operación | Propiedades |
|---|---|
| Suma | |
| Diferencia | |
| Producto | |
| Cociente | 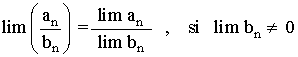 |
| Producto por un número real |


 INICIO
INICIO

