Problemas resueltos de progresiones aritméticas.
1) Tres números en progresión aritmética tienen por suma 33 y su producto es 1232. Halla dichos números.
2) ¿Cuántos términos hay que sumar de la progresión aritmética { 2, 6, 10, 14, .. } para obtener como resultado 288 ?
3) La suma de n términos naturales tomados a partir del 17 es 3024. ¿Cuántos terminos hemos sumado?
4) Se consideran 15 términos de una progresión aritmética. La diferencia entre el primer y último término es 14 y, además, la suma del sexto y el décimo término es 50. Halla el valor de los extremos ( primer y último término ).
5) La suma de 13 términos de una progresión aritmética es 429. Teniendo en cuenta que la diferencia de los extremos es 48, ¿cuáles son los términos de dicha progresión?
6) Las longitudes de los tres lados de un triángulo rectángulo están en progresión aritmética y suman 36 metros. ¿Cuánto mide cada lado?
7) Los tres lados de un triángulo forman una progresión aritmética de razón d. Expresar en función de d el valor de cada uno de ellos. Se supone un triángulo rectángulo.
8) Las longitudes de los lados de un triángulo de 30 cm de perímetro están en progresión aritmética de diferencia cuatro. ¿Cuánto miden los lados del triángulo?
9) Los cinco ángulos de un pentágono forman una progresión aritmética de razón 15º. Determinarlos.
10) Los seis ángulos de un hexágono están en progresión aritmética. Sabiendo que la diferencia entre el mayor y el menor es 50º, calcula el valor de cada ángulo.
11) Halla las dimensiones de un ortoedro sabiendo que están en progresión aritmética, que suman 33 m y que el volumen del ortoedro es 1056 m 3.
1) Tres números en progresión aritmética tienen por suma 33 y su producto es 1232. Halla dichos números.
Sean los números n - d , d y n + d :
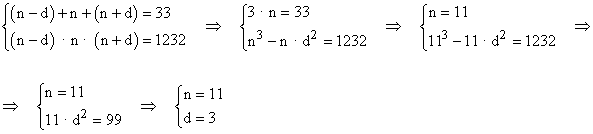
Luego los números son : 8 , 11 y 14
2) ¿Cuántos términos hay que sumar de la progresión aritmética { 2, 6, 10, 14, .. } para obtener como resultado 288 ?
De esta progresión aritmética, a1 = 2 y d = 4, por lo que el término general es an = 2 + ( n - 1 ) · 4.
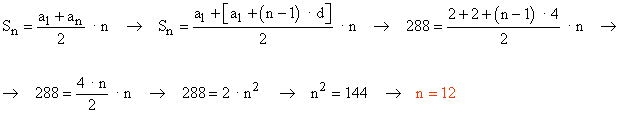
3) La suma de n términos naturales tomados a partir del 17 es 3024. ¿Cuántos terminos hemos sumado?
Como la progresión aritmética está formada por número naturales consecutivos, la diferencia es d = 1.
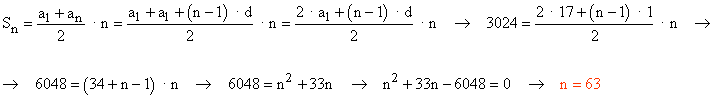
4) Se consideran 15 términos de una progresión aritmética. La diferencia entre el primer y último término es 14 y, además, la suma del sexto y el décimo término es 50. Halla el valor de los extremos ( primer y último término ).
Del enunciado deducimos :
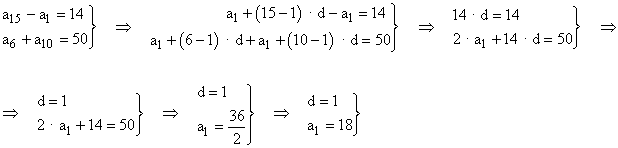
Calculamos por último a15 :
a15 = a1 + ( 15 - 1 ) · 1 = 18 + 14 = 32
Los términos pedidos son : a1 = 18 y a15 = 32
5) La suma de 13 términos de una progresión aritmética es 429. Teniendo en cuenta que la diferencia de los extremos es 48, ¿cuáles son los términos de dicha progresión?
Por los datos del enunciado tenemos que :
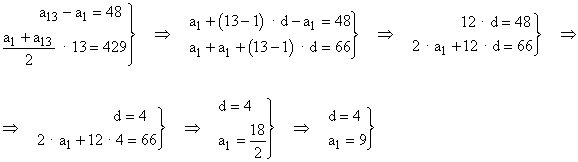
Los términos de la progresión son : 9 , 13 , 17 , 21 , 25 , 29 , 33 , 37 , 41 , 45 , 49 , 53 , 57 .
6) Las longitudes de los tres lados de un triángulo rectángulo están en progresión aritmética y suman 36 metros. ¿Cuánto mide cada lado?
Definiremos los catetos por x y x - d ; la hipotenusa será x + d
Del enunciado tenemos que :
x - d + x + x + d = 36 → 3 · x = 36 → x = 12
Aplicando el teorema de pitágoras podemos encontrar el valor de d :
( 12 - d ) 2 + 12 2 = ( 12 + d ) 2 → 144 + d 2 - 24 · d + 144 = 144 + d 2 + 24 · d → 48 · d = 144 → d = 3
Las medidas de los lados del triángulo son : 9 , 12 , 15 .
7) Los tres lados de un triángulo forman una progresión aritmética de razón d. Expresar en función de d el valor de cada uno de ellos. Se supone un triángulo rectángulo.
Llamamos a los catetos x y x - d y a la hipotenusa x + d . Aplicando el teorema de Pitágoras tenemos que :
( x + d ) 2 = x 2 + ( x - d ) 2 → x 2 + 2 · x · d + d 2 = x 2 + x 2 - 2 · x · d + d 2 → x 2 - 4 · x · d = 0 → x · ( x - 4 · d ) = 0 → x = 4 · d
Los lados del triángulo son : 3d , 4d , 5d
8) Las longitudes de los lados de un triángulo de 30 cm de perímetro están en progresión aritmética de diferencia cuatro. ¿Cuánto miden los lados del triángulo?
Sean a , a + 4 y a + 8 los términos correspondientes a las medidas de los lados de los triángulos.
30 = a + ( a + 4 ) + ( a + 8 ) → 3 · a = 18 → a = 6
Las medidas de los lados del triángulo son : 6 , 9 , 12
9) Los cinco ángulos de un pentágono forman una progresión aritmética de razón 15º. Determinarlos.
La suma de los ángulos de un pentágono es :
S = 180º · ( l - 2 ) = 180º · ( 5 - 2 ) = 540º
Como sumamos los cinco lados, tenemos que calcular el valor de a5 :
a5 = a1 + ( n - 1 ) · d → a5 = a1 + ( 5 - 1 ) · 15º → a5 = a1 + 60º
Por último, de la expresión para calcular la suma en una progresión aritmética tenemos que :
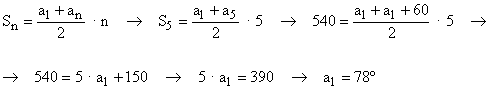
Los ángulos del pentágono son : 78º , 93º , 108º, 123º, 138º
10) Los seis ángulos de un hexágono están en progresión aritmética. Sabiendo que la diferencia entre el mayor y el menor es 50º, calcula el valor de cada ángulo.
La suma de los ángulos de un hexágono es :
S = 180 · ( n - 2 ) = 180 · ( 6 - 2 ) = 180 · 4 = 720º
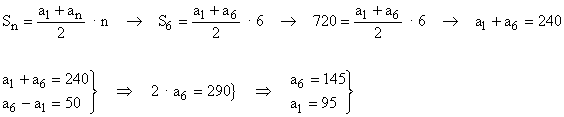
Ahora, a partir de la expresión del término general de una progresión aritmética, obtenemos la diferencia y podemos así calcular el resto de ángulos.
an = a1 + ( n - 1 ) · d → a6 = a1 + ( 6 - 1 ) · d → 145 = 95 + 5 · d → 5 · d = 50 → d = 10
Los ángulos son : 95 , 105 , 115 , 125 , 135 , 145 .
11) Halla las dimensiones de un ortoedro sabiendo que están en progresión aritmética, que suman 33 m y que el volumen del ortoedro es 1056 m 3.
Sean a - d , a y a + d las dimensiones del ortoedro :
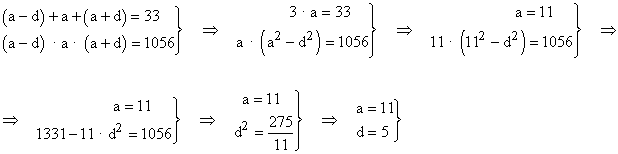
Las dimensiones del ortoedro son : 5 , 11 , 16


 INICIO
INICIO