INICIOSuma y producto de los términos de una progresión geométrica.
La suma de los n primeros términos de una progresión geométrica.
La suma de los n primeros términos de una progresión geométrica se puede calcular mediante la fórmula:
Ejemplo 1 :
Halla la suma de los 10 primeros términos de una progresión geométrica cuya razón es dos y su primer término es cinco.
Calculamos en primer lugar a10 :
a10 = a1 · r n - 1 = 5 · 2 9 = 2560
Aplicamos ahora la fórmula para calcular la suma de los términos de una progresión geométrica :
Suma ilimitada de una progresión geométrica con | r | < 1.
La suma de todos los términos o la suma ilimitada de una progresión geométrica con
| r | < 1, es decir, -1 < r < 1, viene dada por la fórmula:
Ejemplo 2 :
Halla la suma ilimitada de la progresión geométrica 
En primer lugar comprobamos que la razón de la progresión geométrica cumpla que | r | < 1.
En este caso, 
por lo que sí podemos calcular la suma ilimitada.
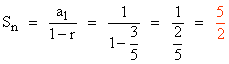
Ejemplo 3 :
Calcula la suma ilimitada de la progresión geométrica 
Tenemos una progresión geométrica cuya razón es 
. Como - 1 < r < 0 decimos que es una función oscilante. Su suma ilimitada sería :
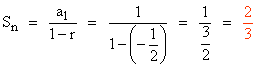
Producto de los n primeros términos de una progresión geométrica.
El producto de los n primeros términos de un aprogresión geométrica viene dada por la fórmula :
Ejemplo 4 :
Halla el producto de los siete primeros términos de la progresión geométrica 3, 9, 27, 81, 243, ...
Calculamos en primer lugar el término a7 y aplicamos la fórmula para calcular el producto de los siete primeros términos.
a7 = a1 · r n - 1 = 3 · 3 6 = 3 7 = 2187
