Sucesiones
Una sucesión es un conjunto ordenado de números reales :
a1, a2, a3, a4, a5 ...
Es una función en que la variable independiente es un número natural y la variable dependiente es un número real.
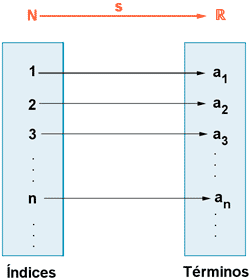
A cada uno de los números que forman la sucesión se le llama término de la sucesión, que es el conjunto imagen y se designa por ai donde i indica el lugar que ocupa en la sucesión, los índices.
Ejemplo 1:
Los números 1, 3, 5, 7, 9, 11, ... son un conjunto de números que están ordenados, y forman una sucesión.
| Lugar | 1º | 2º | 3º | 4º | 5º | 6º | 7º | ... |
|---|---|---|---|---|---|---|---|---|
| Número de la sucesión | 1 | 3 | 5 | 7 | 9 | 11 | 13 | ... |
Se trata de los números impares y la regla que siguen es que cada número se obtiene sumándole 2 unidades al anterior.
Ejemplo 2:
Los números 1, 3, 5, 7, 9, 11, ... son un conjunto de números que están ordenados, y forman una sucesión.
La sucesión se puede representar por a1, a2, a3, a4, a5 ... de donde:
- a1 = 1 → significa que el número 1 ocupa el primer lugar de la sucesión.
- a2 = 3 →significa que el número 3 ocupa el segundo lugar de la sucesión.
- a3 = 5 →significa que el número 5 ocupa el tercer lugar de la sucesión.
- ...
Ejemplo 3:
Determina cuáles son los términos a2 y a4 de la siguientes sucesiónes:
a) 15, 30, 45, 60, 75, ...
b) -2, -4, -6, -8, -10, ...
a) a2 = 30 a4 = 60
b) a2= -4 a4 = -8
Sucesión regular
Una sucesión es regular cuando sigue una determinada regla. Para ello se puede buscar una ley de formación que consiste en dar la ley que genera la sucesión.
Ejemplo 4:
Determina la ley de formación de las siguientes sucesiones:
a) 2, 4, 6, 8, 10, ... ⇒ Cada término es el anterior más dos.
b) 1, 3, 9, 27, 81, 243, ... ⇒ Cada término es el anterior multiplicado por tres.
c) 1, 4, 9, 16, 25, 36, ... ⇒ Cada término es el cuadrado del lugar que ocupa.
d) 1, 2, 5, 9, 14, 20, ... ⇒ Cada término es el anterior más 1, más 2, más 3, ...
e) 1, 8, 27, 64, 125, 216 ⇒ Cada término es el cubo del lugar que ocupa.
Término general
El término general de una sucesión es una expresión que nos permite calcular cualquiér término de la sucesión sabiendo el lugar que ocupa, lo representamos por an.
Ejemplo 5:
Dadas las siguientes sucesiones, hallar el término general:
a) 1, 3, 5, 7, 9, 11, ...
b) 15, 30, 45, 60, 75, ...
c) -2, -4, -6, -8, -10, ...
a) a1 = 2 · 1 - 1 = 1
a2 = 2 · 2 - 1 = 3
a3 = 2 · 3 - 1 = 5
a4 = 2 · 4 - 1 = 7
...
an = 2 · n -1
b) a1 = 15
a2 = 15 + 15 · 1= 30
a3 = 15 + 15 · 2 = 45
a4 = 15 + 15 · 3 = 60
...
an = 15 + 15 · (n-1)
c) a1 = -2 · 1 = -2
a2 = -2 · 2 = -4
a3 = -2 · 3 = -6
a4 = -2 · 4 = -8
...
an = -2 · n
Ejemplo 6:
Calcula los cuatro primeros términos de las siguientes sucesiones:
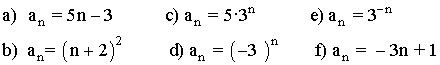
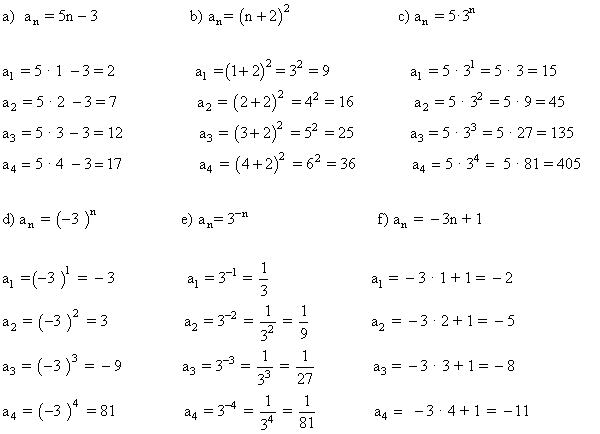
Ejemplo 7:
Halla los seis primeros términos de las sucesiones siguientes y calcula mentalmente la fórmula del término general:
a) Múltiplos de cinco.
b) Números pares.
c) Cuadrados perfectos.
d) Números impares.
e) Cubos perfectos. f) Los inversos de los cuadrados de los números naturales.
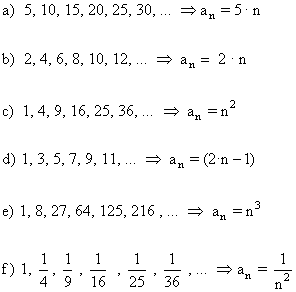


 INICIO
INICIO
