Sucesión de Fibonacci.
Sucesiones recurrentes
Una sucesión es recurrente cuando cada término a partir de uno dado se obtiene de los anteriores.
Ejemplo 1:
Encuentra el término general de la sucesión y calcula a7 y a8 :
1, 3, 5, 7, 9, 11, ...
Cada término es el anterior más dos unidades.
a1 = 1
a2 = a1 + 2 = 3
a3 = a2 + 2 = 5
a4 = a3 + 2 = 7
...
an = an - 1 + 2
Cada número es el anterios más dos.
a7 = a6 + 2 = 11 + 2 = 13
a8 = a7 + 2 = 13 + 2 = 15
Ejemplo 2:
Obtener los seis primeros términos de cada sucesión:
![]()
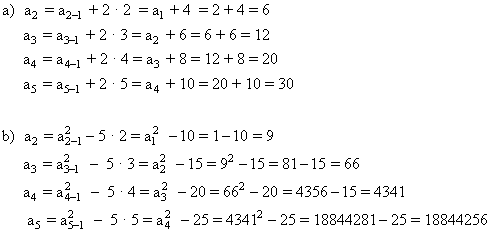
Sucesión de Fibonacci.
La sucesión de Fibonacci es una sucesión recurrente definida de la siguiente forma :
a1 = 1 a2 = 1 an = an - 2 + an - 1
Cada término, a partir del tercero, se obtiene sumando los dos anteriores.
Ejemplo 3 :
Escribe los diez primeros términos de la sucesión de Fibonacci.
a1 = 1
a2 = 1
a3 = a3 - 2 + 3 - 1 = a1 + a2 = 1 + 1 = 2
a4 = a4 - 2 + a 4 - 1 = a2 + a3 = 1 + 2 = 3
a5 = a5 - 2 + a 5 - 1 = a3 + a4 = 1 + 2 = 5
a6 = a6 - 2 + a 6 - 1 = a4 + a5 = 3 + 5 = 8
a7 = a7 - 2 + a 7 - 1 = a5 + a6 = 5 + 8 = 13
a8 = a8 - 2 + a 8 - 1 = a6 + a7 = 8 + 13 = 21
a9 = a9 - 2 + a 9 - 1 = a7 + a8 = 13 + 21 = 34
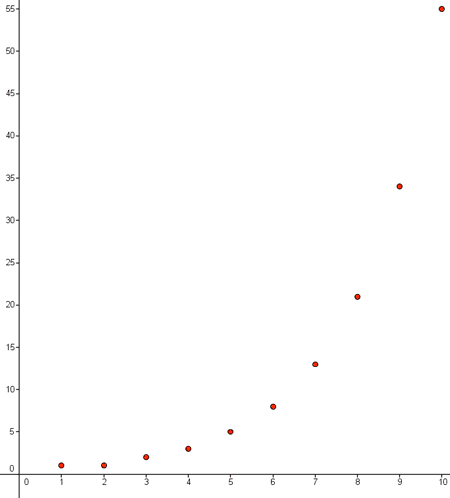
a10 = a10 - 2 + a 10 - 1 = a8 + a9 = 21 + 34 = 55
| Lugar | Número de la sucesión |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |


 INICIO
INICIO

