Ejercicios resueltos de progresiones aritméticas.

1)     Encuentra el término general de las siguientes progresiones aritméticas :
a)    3,  7,  11,  15,  ...
b)   
c)    24,  16,  8,  0,  ...
d)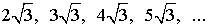   

2)     Escribe los cinco primeros términos y   a₁₅   de las siguientes progresiones aritméticas :
a)    a₁ = 3,2   y   d = 3
b)    a₁ = 7   y   d = - 5
c)    a₁ =   y   r =
d)    a₁ = - 11   y   r = 6

3)    Hallar los términos que se indican en las siguientes progresiones aritméticas :
a)    a₁₀,  a₁₂  y  a₂₀   en    2, 5, 8, 11, ...
b)    a₈,  a₁₁  y  a₁₅     en     9, 11, 13, 15, ...
c)    a₇,  a₃₀  y  a₅₀     en     -20, -15, -10, ...

4)    Halla el término general de una progresión aritmética sabiendo que   a₅ = 19   y   a₁₁ = 43.

5)    Sabiendo que   a₅ = -1   y   a₉ = 1,   calcular el término general de dicha progresión geométrica.

6)    El primer término de una progresión aritmética es  11  y la diferencia es  - 4.  ¿Qué lugar ocupa el número  - 45 ? ¿Y el  - 17 ?

7)    Dada la progresión aritmética de término general     calcula la suma de los 20 primeros términos.

8)    Calcula la suma de los términos  a₈  hasta  a₃₂  de una progresión aritmética sabiendo que el término general es   a_n = - 10 + (n - 1 ) · 2.

9)    Calcula la suma de los  25  primeros términos de una progresión aritmética sabiendo que  a₄ = 7  y  a₁₀ = 25.

10)    Dada una progresión aritmética, interpola los términos que se piden :
a)    Cinco términos entre el  4  y el  34.
b)    Cuatro términos entre el  - 3  y el  32.

1)     Encuentra el término general de las siguientes progresiones aritméticas :
a)    3, 7, 11, 15, ...
b)   
c)    24, 16, 8, 0, ...
d)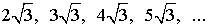   

a)
a₁  =  3   y   d  =  4     →     a_n  =  a₁  +  ( n  -  1 )  ·  d     →     a_n  =  3  +  ( n  -  1 )  ·  4    →     a_n  =  4  ·  n  -  1

b)
a₁  =    y   r  =      →     a_n  =  a₁  +  ( n  -  1 )  ·  r     →     a_n  =   +  ( n  -  1 )  ·      →     a_n  =     ·  n

c)
a₁  =  24   y   r  =  - 8     →     a_n  =  a₁  +  ( n  -  1 )  ·  r     →     a_n  =  24  +  ( n  -  1 )  ·  ( - 8 )     →     a_n  =  32  -  8  ·  n

d)
a₁  =    y   r  =      →     a_n  =  a₁  +  ( n  -  1 )  ·  r     →    a_n =    +  ( n  -  1 )  ·      →     a_n  = 

2)     Escribe los cinco primeros términos y   a₁₅   de las siguientes progresiones aritméticas :
a)    a₁ = 3,2   y   d = 3
b)    a₁ = 7   y   d = - 5
c)    a₁ =   y   r =
d)    a₁ = - 11   y   r = 6

a)
a₂  =  6,2  ;   a₃  =  9,2  ;   a₄  =  12,2  ;   a₅  =  15,2  
a_n  =  a₁  +  ( n  -  1 )  ·  d    →    a₁₅  =  3,2  +  ( 15  -  1 )  ·  3    →    a₁₅  =  45,2

b)
a₂  =  2  ;   a₃  =  - 3  ;   a₄  =  - 8  ;   a₅  =  - 13
a_n  =  a₁  +  ( n  -  1 )  ·  d    →    a₁₅  =  7  +  ( 15  -  1 )  ·  ( - 5 )    →    a₁₅  =  - 63

c)
a₂  =  1  ;   a₃  =    ;   a₄  =  0  ;   a₅  = 
a_n  =  a₁  +  ( n  -  1 )  ·  d    →    a₁₅  =   +  ( 15  -  1 )  ·     →    a₁₅  = 

d)
a₂  =  5    ; a₃  =  11  ;   a₄  =  17  ;   a₅  =  23
a_n  =  a₁  +  ( n  -  1 )  ·  d    →    a₁₅  =  - 11  +  ( 15  -  1 )  ·  6    →    a₁₅  =  73

3)    Hallar los términos que se indican en las siguientes progresiones aritméticas :
a)    a₁₀,  a₁₂  y  a₂₀   en    2, 5, 8, 11, ...
b)    a₈,  a₁₁  y  a₁₅     en     9, 11, 13, 15, ...
c)    a₇,  a₃₀  y  a₅₀     en     -20, -15, -10, ...

Al ser progresiones artiméticas, su término general es  a_n  =  a₁ + ( n - 1 ) · d.   Calcularemos en cada uno de los casos su término general y luego los términos que nos piden.

4)    Halla el término general de una progresión aritmética sabiendo que   a₅ = 19   y   a₁₁ = 43.

Al ser una progresión aritmética, el término general es   a_n = a₁ + ( n - 1 ) · d.   Sustituyendo los datos del enunciado tenemos :



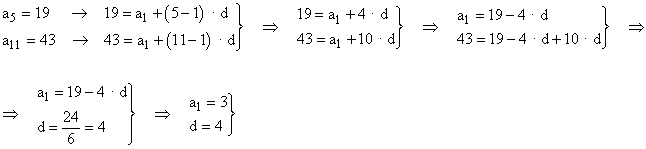
El término general de la progresión aritmética es :

a_n = 3 + ( n - 1 ) · 4

5)    Sabiendo que   a₅ = -1   y   a₉ = 1,   calcular el término general de dicha progresión geométrica.

Al ser una progresión aritmética, el término general viene determinado por   a_n = a₁ + ( n - 1 ) · d.   Sustituyendo los datos del enunciado tenemos :



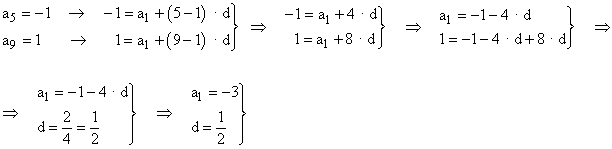
El término general de la sucesión es :

a_n = - 3 + ( n - 1 ) ·

6)    El primer término de una progresión aritmética es  11  y la diferencia es  - 4.  ¿Qué lugar ocupa el número  - 45 ? ¿Y el  - 17 ?

El término general de la progresión aritmética es   a_n = 11 + ( n - 1 ) · ( - 4 ).

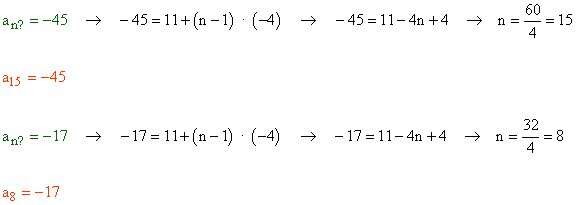
7)    Dada la progresión aritmética de término general     calcula la suma de los 20 primeros términos.

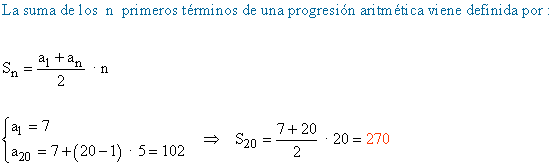
8)    Calcula la suma de los términos  a₈  hasta  a₃₂  de una progresión aritmética sabiendo que el término general es   a_n = - 10 + (n - 1 ) · 2.

9)    Calcula la suma de los  25  primeros términos de una progresión aritmética sabiendo que  a₄ = 7  y  a₁₀ = 25.

Calcularemos en primer lugar el término general de la progresión, para posteriormente determinar  a₂₅  y la suma de los primeros  25  términos.

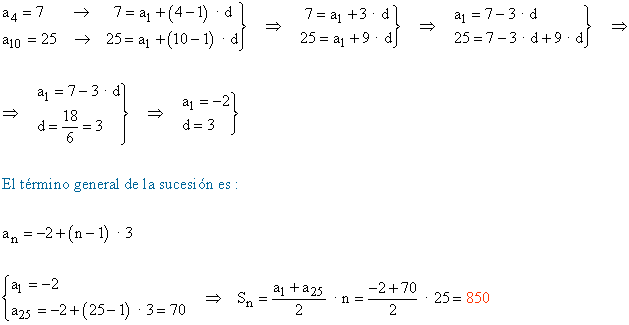
10)    Dada una progresión aritmética, interpola los términos que se piden :
a)    Cinco términos entre el  4  y el  34.
b)    Cuatro términos entre el  - 3  y el  32.

a)
Como tenemos que interpolar cinco términos, tomamos  a₁ = 4  y  a₇ = 34.
Calculamos en primer lugar  d :

a_n = a₁ + ( n - 1 ) · d    →    34 = 4 + ( 7 - 1 ) · d    →    30 = 6 · d    →    d = 5

De forma análoga, podemos calcularlo mediante la expresión    donde   a = 4,  b = 34   y   k = 5  ( número de términos a interpolar ) :



Los términos interpolados serían :    4,  9,  14,  19,  24,  29,  34

b)
Tenemos que interpolar cuatro términos, por lo que tomamos  a₁ = - 3  y  a₆ = 32.
En primer lugar calculamos  d,  por cualquiera de los métodos anteriores :

a_n = a₁ + ( n - 1 ) · d    →    32 = - 3 + ( 6 - 1 ) · d    →    35 = 5 · d    →    d = 7

O bien, tomando  a = - 3,  b = 32  y  k = 4  en la siguiente expresión :



Los términos interpolados serían :      - 3,  4,  11,  18,  25,  32.