Problemas resueltos de regla de tres compuesta
1) Un colegio ha necesitado 25 Kg de fruta para alimentar a 300 alumnos durante una semana.
¿Cuántos kilos necesitará para alimentar a 200 alumnos en 30 días?
2) Un grupo de albañiles trabajando 8 horas diarias construyen 600 m² de pared en 10 días.
¿Cuánto tardaría la misma cuadrilla en construir 1000 m² de pared si deciden trabajar 12 horas diarias?
3) Durante 30 días ocho obreros han reparado 200 metros de cableado eléctrico. Calcula cuántos metros de cableado repararán quince obreros en 20 días.
4) Un profesor corrige exámenes durante dos horas diarias a razón de seis exámenes por horas, y tarda 12 días. Si corrigiese durante cuatro horas diarias a razón de nueve exámenes por hora, ¿cuántos días tardaría en corregir los mismos exámenes?
5) En una semana, tres máquinas han excavado un pozo de 120 metros de profundidad. ¿Cuántas máquinas serían necesarias para excavar un pozo de 1000 metros durante cinco días?
6) En una fábrica, dos máquinas producen tornillos, trabajando cinco días a la semana durante cuatro horas diarias. Su producción es de 1000 tornillos. ¿Cuántas horas diarias tendrían que trabajar tres máquinas durante seis cuatro días a la semana para producir 1200 tornillos?
7) Los gastos en alimentación de 153 personas son 2550 € diarios. Calcula cuántas personas podrían alimentarse durante 60 días con 10000 €.
8) En una cadena de montaje, 15 operarios trabajando 6 horas a la semana, ensamblan 820 frigoríficos. Si quieren aumentar la producción a 1200 unidades, ¿cuántas horas diarias necesitarán trabajar teniendo en cuenta que se incorporarán 5 trabajadores más?
9) En un terreno de 320 metros de largo y 95 metros de ancho hemos recogido una cosecha de 5500 kg de lechuga. ¿Qué cosecha podríamos recoger de otro campo de 270 metros de largo y 120 metros de ancho?
10) En una granja de 1740 gallinas, se gastan semalnalmente 650 € en productos y compuestos para su mantenimiento. ¿Cuántos días serían necesarios para tener unos gastos de 800 € con 2100 gallinas?
11)
12)
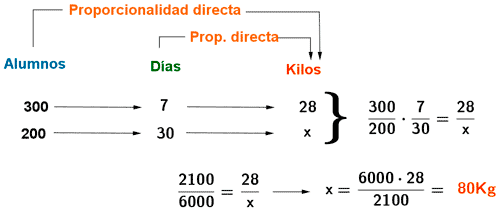
1) Un colegio ha necesitado 25 Kg de fruta para alimentar a 300 alumnos durante una semana.
¿Cuántos kilos necesitará para alimentar a 200 alumnos en 30 días?
Cuanto menos alumnos menos kilos de fruta necesitamos, por tanto es una relación directa.
Cuantos más días más kilos se necesitan, por tanto es una relación directa.
Para resolver la regla de tres compuesta: operamos en cruz según se ve en el dibujo.
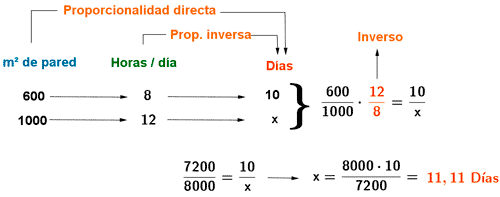
2) Un grupo de albañiles trabajando 8 horas diarias construyen 600 m² de pared en 10 días.
¿Cuánto tardaría la misma cuadrilla en construir 1000 m² de pared si deciden trabajar 12 horas diarias?
Cuanto más m² de pared más días se trabajan, por tanto es una relación directa.
Cuantas más horas se trabajan menos días se necesitan, por tanto es una relación inversa.
Para resolver la regla de tres compuesta: operamos en cruz según se ve en el dibujo.
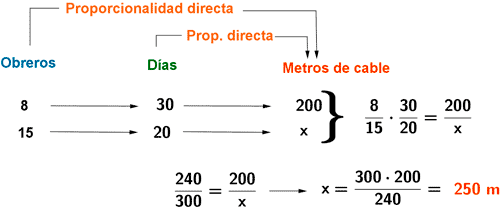
3) Durante 30 días ocho obreros han reparado 200 metros de cableado eléctrico. Calcula cuántos metros de cableado repararán quince obreros en 20 días.
La relación entre el número de días y los metros de cableado es directa, ya que a menos número de días trabajando, menor número de metros de cable reparado.
El número de obreros también tiene una relación directa con el número de metros de cabñe, ya que a mayor cantidad de obreros, mayor cantidad de metros de cable podrán reparar.
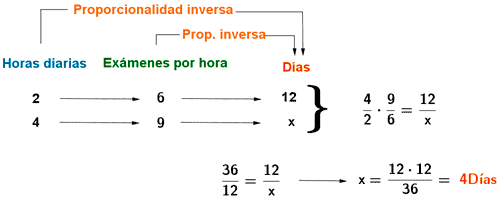
4) Un profesor corrige exámenes durante dos horas diarias a razón de seis exámenes por horas, y tarda 12 días. Si corrigiese durante cuatro horas diarias a razón de nueve exámenes por hora, ¿cuántos días tardaría en corregir los mismos exámenes?
En este caso, la relación entre el número de horas diarias y el número de exámenes corregidas es nversa, ya que a mayor cantidad de horas diarias, menos días tardaría.
Ocurre lo mismo con el número de exámenes por hora y el número de días. Si corrige más exámenes por hora, el número de días que tardaría en corregirlos sería menor.
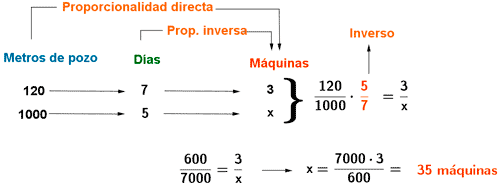
5) En una semana, tres máquinas han excavado un pozo de 120 metros de profundidad. ¿Cuántas máquinas serían necesarias para excavar un pozo de 1000 metros durante cinco días?
La relación que exite entre el número de máquinas y la profundidad del pozo es directa, ya que a mayor número de máquinas, más metros de pozo pueden excavarse.
Sin embargo, la relación entre el número de máquinas y el número de días es inverso, ya que si trabajan más máquinas, el número de días que tardarían es menor.
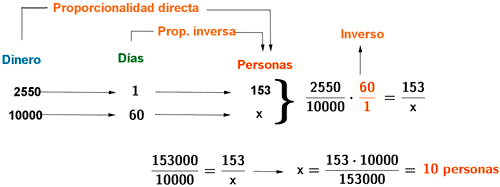
6) Los gastos en alimentación de 153 personas son 2550 € diarios. Calcula cuántas personas podrían alimentarse durante 60 días con 10000 €.
La relación entre el número de personas y los gastos es una relación directa, ya que a mayor número de personas, el gasto también será mayor.
Sin embargo, el número de días y el número de personas es una relación inversa : cuánto mayor sea el número de días que tengo que alimentar, menor será la cantidad de personas que pueda alimentar.
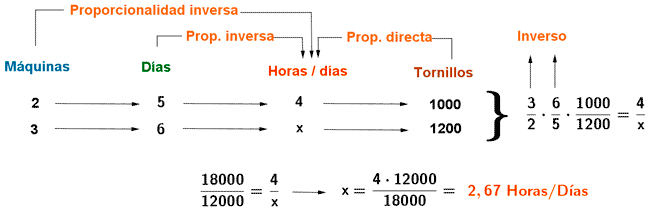
7) En una fábrica, dos máquinas producen tornillos, trabajando cinco días a la semana durante cuatro horas diarias. Su producción es de 1000 tornillos. ¿Cuántas horas diarias tendrían que trabajar tres máquinas durante seis cuatro días a la semana para producir 1200 tornillos?
La relación que existe entre el número de horas y la cantidad de tornillos es directa, ya que a mayor cantidad de horas trabajando, mayor cantidad de tornillos se producen.
Sin embargo, tanto el número de máquinas como el número de días tienen una relación inversa respecto al número de horas, ya que a mayor número de máquinas días trabajados, menos horas funcionan las máquinas.
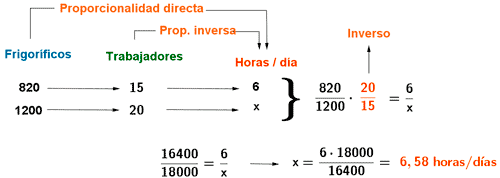
8) En una cadena de montaje, 15 operarios trabajando 6 horas a la semana, ensamblan 820 frigoríficos. Si quieren aumentar la producción a 1200 unidades, ¿cuántas horas diarias necesitarán trabajar teniendo en cuenta que se incorporarán 5 trabajadores más?
La relación que existe entre el número de horas y la cantidad de frigoríficos ensamblados es directa, ya que cuanto mayor sea el número de horas, más frigoríficos podrán ensamblarse.
Por otro lado, la relación entre el número de horas y el número de trabajdores es inversa, puesto que si tenemos más trabajdores, las horas que necesitarán para ensamblar es menor.
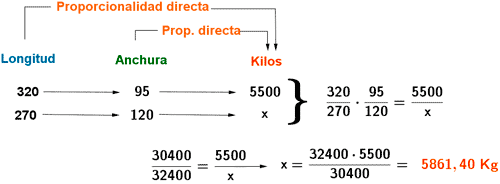
9) En un terreno de 320 metros de largo y 95 metros de ancho hemos recogido una cosecha de 5500 kg de lechuga. ¿Qué cosecha podríamos recoger de otro campo de 270 metros de largo y 120 metros de ancho?
La relación existente entre las dimensiones del terreno y la cosecha recogida es directa en ambos casos, tanto para la longitud del terreno como para su anchura.
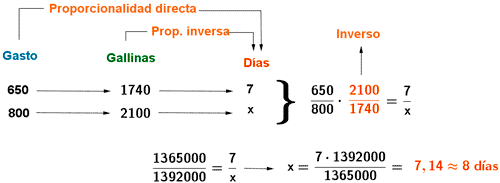
10) En una granja de 1740 gallinas, se gastan semalnalmente 650 € en productos y compuestos para su mantenimiento. ¿Cuántos días serían necesarios para tener unos gastos de 800 € con 2100 gallinas?
El número de gallinas y el número de días tiene una relación inversa, ya que a mayor número de días, menor cantidad de gallinas pueden mantenerse.
Sin embargo, el número de días y el gasto en euros tienen una relación directa : a mayor número de días, el gasto en productos es mayor.
11
12


 INICIO
INICIO