Problemas resueltos de regla de tres.
1) De un pozo hemos extraído 120 litros en 10 minutos. ¿Cuántos litros extraeremos en 25 minutos?
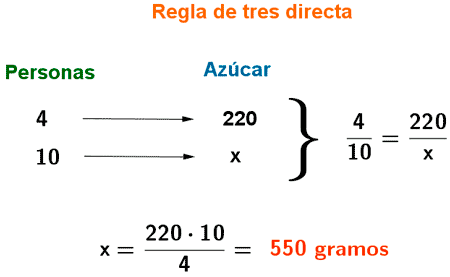
2) Para hacer un bizcocho para cuatro personas necesitamos 220 gramos de azúcar. Si queremos hacer un bizcocho para 10 personas, ¿qué cantidad de azúcar necesitamos?
3) Los vecinos de una urbanización pagan 230 € al mes por la factura de la luz de 80 farolas. Si se desea reducir el gasto a 175 €, ¿cuántas farolas debemos quitar?
4) Un grifo tarda 4 horas y 25 minutos en llenar un depósito de 1300 litros. ¿Cuántos litros aporta el grifo a la semana?
5) Un peregrino del Camino de Santiago ha empleado 4 días y 3 horas en recorrer una distancia de 106 kilómetros. Teniendo en cuenta que cada día camina durante seis horas, ¿qué distancia ha recorrido diariamente?
6) Seis personas recogen los tomates de un huerto en siete horas. ¿Cuánto tiempo tardarían en recoger el mismo huerto ocho personas?
7) Un tren de cercanías tarda 1 hora y 15 minutos en completar su trayecto a una velocidad de 80 km/h. ¿Cuánto tiempo tardaría si aumentase su velociad a 110 km/h ?
8) Un campamento de refugiados que acoge a 2300 personas tiene víveres suficientes para abastecerse durante 22 semanas. Si llegan al campamento 320 refugiados más, ¿En cuánto se reducirá el tiempo para el que tienen víveres?
9) En un concurso televisivo cada concursante se lleva un premio en función de los fallos que cometa : a menos fallos, mayor es el premio recibido. Teniendo en cuenta que un concursante ha ganado 2500 € cometiendo ocho fallos, ¿cuál es el premio de un concursante con sólo tres fallos?
10) Una finca está rodeada por una valla antigua formada por 1024 postes separados 90 centímetros unos de otros. Se quiere colocar una nueva valla, en este caso, formada por postes separados 1,60 metros unos de otros. ¿Qué cantidad de postes necesitaré para esta nueva valla?
11)
12)
1) De un pozo hemos extraído 120 litros en 10 minutos. ¿Cuántos litros extraeremos en 25 minutos?
Resolveremos este problema planteando una regla de tres. En este caso, la regla de tres es directa, ya que extraeremos mayor cantidad de agua si empleamos más tiempo para ello : a mayor tiempo, más agua.

2) Para hacer un bizcocho para cuatro personas necesitamos 220 gramos de azúcar. Si queremos hacer un bizcocho para 10 personas, ¿qué cantidad de azúcar necesitamos?
Resolveremos el problema mediante una regla de tres. La regla de tres es, en este caso, directa, ya que para hacer un bizcocho para más personas necesitaremos más azúcar.
3) Los vecinos de una urbanización pagan 230 € al mes por la factura de la luz de 80 farolas. Si se desea reducir el gasto a 175 €, ¿cuántas farolas debemos quitar?
Resolvemos el problema mediante una regla de tres directa, ya que a mayor número de farolas, mayor es el gasto en euros.
En primer lugar, calculamos el número de farolas que podríamos tener con 175 €, para posteriormente saber cuántas tenemos que eliminar.
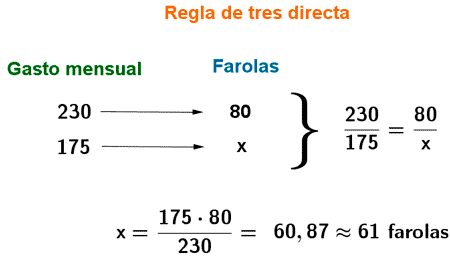
Debemos eliminar por lo tanto : 80 - 61 = 19 farolas
4) Un grifo tarda 4 horas y 25 minutos en llenar un depósito de 1300 litros. ¿Cuántos litros aporta el grifo a la semana?
Tenemos una regla de tres directa, ya que a mayor cantidad de días, el agua que aporta el grifo es mayor.
4 horas y 25 minutos = 4 · 60 + 25 = 265 minutos
1 semana = 7 · 24 · 60 = 10080 minutos
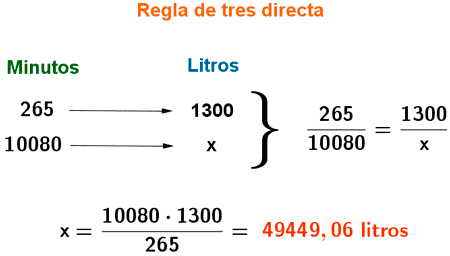
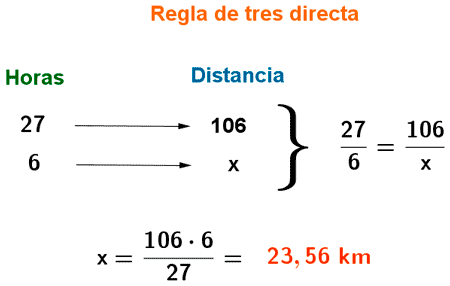
5) Un peregrino del Camino de Santiago ha empleado 4 días y 3 horas en recorrer una distancia de 106 kilómetros. Teniendo en cuenta que cada día camina durante seis horas, ¿qué distancia ha recorrido diariamente?
Como la distancia recorrida y el número de días son directamente proporcionales, calculamos mediante una regla de tres directa la distancia que ha recorrido en cada día.
4 días y 3 horas = 4 · 6 + 3 = 27 horas.
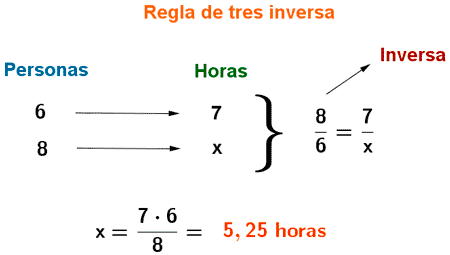
6) Seis personas recogen los tomates de un huerto en siete horas. ¿Cuánto tiempo tardarían en recoger el mismo huerto ocho personas?
Resolveremos el problema mediante una regla de tres. En este caso, la relación entre ambas magnitudes es inversa, ya que a mayor número de personas, el tiempo que tardarán en recoger el huerto será menor.
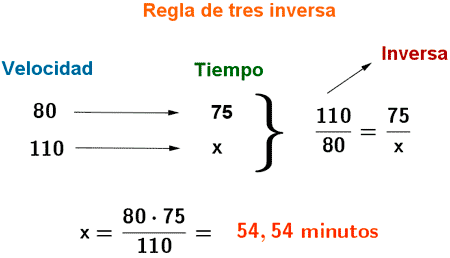
7) Un tren de cercanías tarda 1 hora y 15 minutos en completar su trayecto a una velocidad de 80 km/h. ¿Cuánto tiempo tardaría si aumentase su velociad a 110 km/h ?
Tenemos una relación inversa, ya que si la velocidad del tren es mayor, el tiempo que tardará en recorrer la distancia será menor. Resolvemos por tanto el problema por una regla de tres inversa.
1 hora y 15 minutos = 60 + 15 = 75 minutos.
8) Un campamento de refugiados que acoge a 2300 personas tiene víveres suficientes para abastecerse durante 22 semanas. Si llegan al campamento 320 refugiados más, ¿En cuánto se reducirá el tiempo para el que tienen víveres?
Resolveremos el problema mediante una regla de tres. Dado que el número de refugiados y el tiempo de víveres, son inversamente proporcionales ( cúantos más refugiados haya, menor tiempo durarán los víveres ) emplearemos una regla de tres inversa.
2300 + 320 = 2620 refugiados
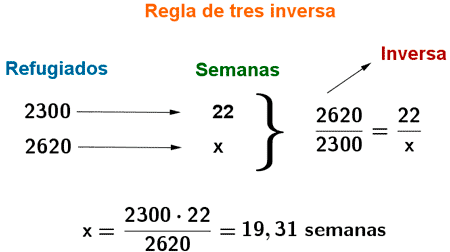
Tendremos víveres para 2,69 semanas menos.
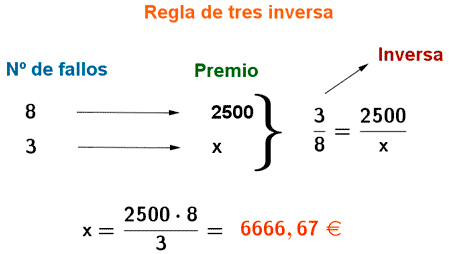
9) En un concurso televisivo cada concursante se lleva un premio en función de los fallos que cometa : a menos fallos, mayor es el premio recibido. Teniendo en cuenta que un concursante ha ganado 2500 € cometiendo ocho fallos, ¿cuál es el premio de un concursante con sólo tres fallos?
Como nos explican en el enunciado, la relación fallos-premio es inversa, por lo que para resolver el problema emplearemos una regla de tres inversa.
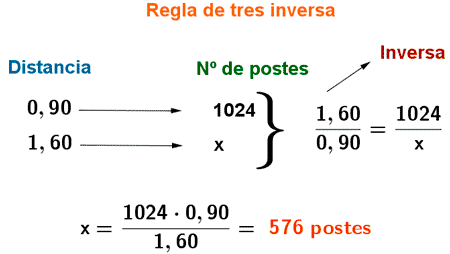
10) Una finca está rodeada por una valla antigua formada por 1024 postes separados 90 centímetros unos de otros. Se quiere colocar una nueva valla, en este caso, formada por postes separados 1,60 metros unos de otros. ¿Qué cantidad de postes necesitaré para esta nueva valla?
La relación existente entre el número de postes y la distancia entre estos es inversa : cuánto mayor sea la distancia entre los postes, menos cantidad de postes necesitaré para vallar la finca. Resolveremos el problema mediante una regla de tres inversa.
90 centímetros = 0,90 metros.
11
12


 INICIO
INICIO