Representación de funciones exponenciales
Resumen de las propiedades de la función exponencial ex
| 1 | La función exponencial es la inversa de la logarítmica: y = ex ⇔ x = Ln y |
|---|---|
| 2 | La función y = ex tiene por dominio R y por recorrido y > 0 |
| 3 | La función y = ex es continua, creciente e inyectiva en todo su dominio. |
| 4 | La función y = ex es cóncava hacia arriba en todo su dominio. |
| 5 | |
Representa gráficamente la función:
![]()
Función exponencial.
Al tratarse de una función exponencial el dominio es toda la recta real:
• Dom(f) = R
Para hallar el recorrido de la función, invertimos las variables y calculamos el dominio de la variable y :
• Im(f) = [0, 1/e]
Continuidad y tipos de discontinuidad
La función es continua en R .
• Corte con el eje OX: f(x) = 0
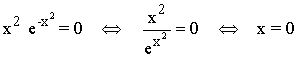
El punto de corte es: (0, 0)
• Corte con el eje OY: f(0)
![]()
El punto de corte es: (0, 0)
Como el puntos de corte con el eje OX es x = 0 , tenemos que estudiar los siguientes intervalos: (-∞, 0) , (0, +∞) :
| Intervalo | (-∞, 0) | (0, +∞) |
|---|---|---|
| Punto de prueba | f(-3) > 0 | f(3) > 0 |
| Signo de f (x) | + | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
![]()
Por lo tanto la función es simétrica respecto al eje OY .
No es periódica porque las funciones exponenciales nunca lo son.
Asíntotas
Nuestra función se puede escribir de la siguiente forma:
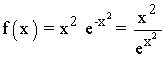
El denominador no se anula nunca. Además, el dominio de la función es toda la recta real, por lo que no existen asíntotas verticales.
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
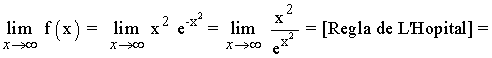
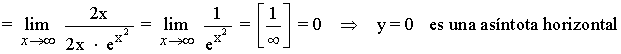
A continuación calculamos la posición relativa de la curva respecto a la asíntota horizontal:
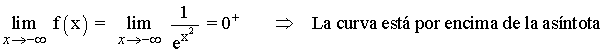
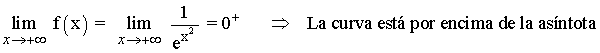
Como la función tiene una asíntota horizontal, entonces no puede tener asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
La primera derivada se anula cuando se anula el segundo miembro, puesto que el primero no se anula para ningún valor de x .
2x - 2x3 = 0 ⇔ 2x(1 - x2) = 0 ⇔ 2x = 0 o 1 = x2 ⇔ x = 0 x = -1 x = 1
Por lo tanto tenemos que estudiar los siguientes intervalos: (-∞, -1) , (-1, 0) , (0, 1) , (1, +∞)
| Intervalo | (-∞, -1) | (-1, 0) | (0, 1) | (1, +∞) |
|---|---|---|---|---|
| Punto de prueba | f ' (-3) > 0 | f ' (-0,5) < 0 | f ' (0,5) > 0 | f ' (3) < 0 |
| Signo de f ' (x) | + | - | + | - |
| Monotonía | Crece | Decrece | Crece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = -1 x = 0 y x = 1 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda:
![]()
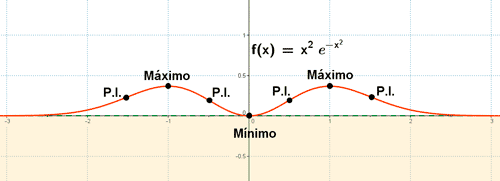
• f '' (-1) < 0 ⇒ Hay un máximo en x = -1 ⇒ f(-1) = 1/e ⇒ Max (-1, 1/e)
• f '' (0) > 0 ⇒ Hay un mínimo en x = 0 ⇒ f(0) = 0 ⇒ Min (0, 0)
• f '' (+1) < 0 ⇒ Hay un máximo en x = +1 ⇒ f(+1) = 1/e ⇒ Max (1, 1/e)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
![]()
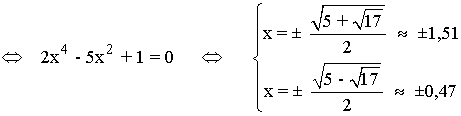
Por lo tanto tenemos que estudiar los siguientes intervalos : (-∞, -1,51) , (-1,51, -0,47) , (-0,47, 0,47), (0,47, 1,51), (1,51, +∞)
| Intervalo | (-∞, -1,51) | (-1,51, -0,47) | (-0,47, 0,47) | (0,47, 1,51) | (1,51, +∞) |
|---|---|---|---|---|---|
| Punto de prueba | f '' (-3) > 0 | f '' (-1) < 0 | f '' (0) > 0 | f '' (1) < 0 | f '' (3) > 0 |
| Signo de f '' (x) | + | - | + | - | + |
| Curvatura | Concava (∪) | Convexa (∩) | Concava (∪) | Convexa (∩) | Concava (∪) |
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son:
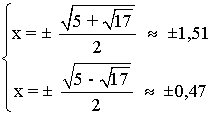
Vamos a determinar a través de la tercera derivada si se trata de puntos de inflexión:
![]()
![]()
La tercera derivada no se anula para ninguno de los puntos anteriores, por lo tanto, todos ellos son puntos de inflexión.
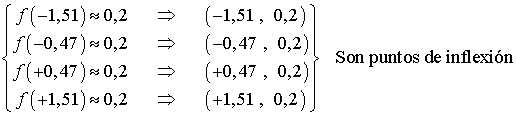


 INICIO
INICIO

