Representación de funciones irracionales
Representa gráficamente la función:
![]()
Función irracional.
Al tratarse de una función irracional (de raiz n par) tenemos que estudiar los valores donde el radicando es mayor o igual que 0.
x2 - 4 ≥ 0 ⇒ Calculamos las raíces de la ecuación ⇒ x2 = 4 ⇒ x = ±√4 = ±2
Por lo tanto, estudiamos el signo del radicando en los intervalos: (-∞, -2) , (-2, 2) y (2, +∞) :
| Intervalo | (-∞, -2] | [-2, 2] | [2, +∞) |
|---|---|---|---|
| Punto de prueba | x = -3 | x = 0 | x = 3 |
| Signo | + | - | + |
Es decir, el signo del radicando es negativo en el intervalo (-2, 2) .
• Dom(f) = R - (-2, 2) = (-∞, -2] ∪ [2, +∞)
• Im(f) = R+ = [0, +∞)
Continuidad y tipos de discontinuidad
La función es continua en R - (-2, 2) , es decir, es discontinua en el intervalo (-2, 2) .
La discontinuidad es de segunda especie o parabólica.
• Corte con el eje OX: f(x) = 0
![]()
El punto de corte es: (-2, 0) y (2, 0)
• Corte con el eje OY: f(0)
La función no está definida en x = 0 , por lo tanto la función no corta al eje OY.
Como los puntos de corte con el eje OX son x = -2 y x = 2 , tenemos que estudiar los siguientes intervalos: (-∞, -2) , y (2, +∞) :
| Intervalo | (-∞, -2) | (2, +∞) |
|---|---|---|
| Punto de prueba | f(-3) > 0 | f(3) > 0 |
| Signo de f (x) | + | + |
En la gráfica se marcan los puntos de corte con los ejes, los puntos de distintinuidad y las regiones donde no hay curva.
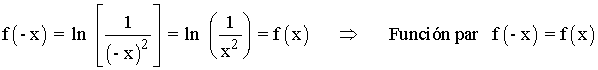
Por lo tanto la función es simétrica respecto al eje OY .
No es periódica porque las funciones irracionales nunca lo son.
Asíntotas
La función no tiene asíntotas verticales.
Para hallar las asíntotas horizontales tenemos que estudiar los límites de la función en el infinito:
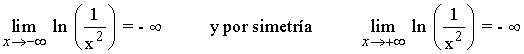
Por lo tanto no tiene asíntotas horizontales.
Para hallar las asíntotas oblicuas calculamos los siguientes límites:
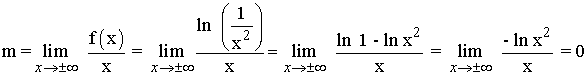
Por lo tanto la función no tiene asíntotas oblicuas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
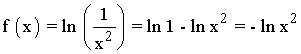
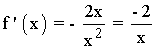
La primera derivada no se anula, por lo tanto estudiamos los intervalos que nos da la discontinuidad de la función: (-∞, -0) , (0, +∞)
| Intervalo | (-∞, 0) | (0, +∞) |
|---|---|---|
| Punto de prueba | f ' (-3) < 0 | f ' (3) > 0 |
| Signo de f ' (x) | + | - |
| Monotonía | Crece | Decrece |
Como la primera derivada no se anula para ningún valor, la función no tiene ni máximos ni mínimos relativos.
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
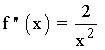
Como ningún valor anula a la segunda derivada, tenemos que estudiar los siguientes intervalos según la continuidad de la función: (-∞, 0) , (0, +∞)
| Intervalo | (-∞, -2) | (2, +∞) |
|---|---|---|
| Punto de prueba | f '' (-3) > 0 | f '' (3) > 0 |
| Signo de f '' (x) | + | + |
| Curvatura | Concava (∪) | Concava (∪) |
Punto de inflexión
Por el apartado anterior sabemos que la segunda derivada no se anula para ningún valor, por lo tanto la función no tiene puntos de inflexión.
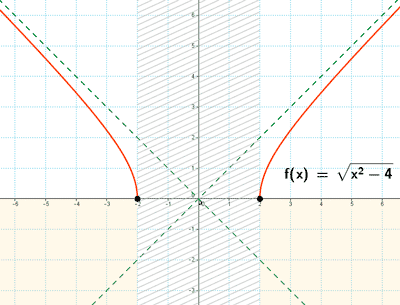


 INICIO
INICIO

