Problemas resueltos de estudio de una función
1) Estudia el dominio y recorrido de las siguientes funciones.
a)
b)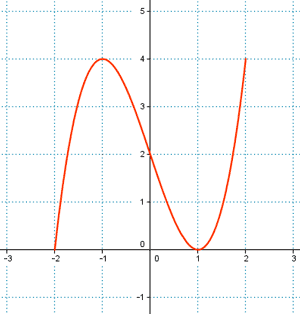
c)
d)
2) Estudia la continuidad o discontinuidad de las siguientes funciones.
a)
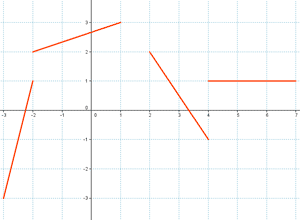
b)
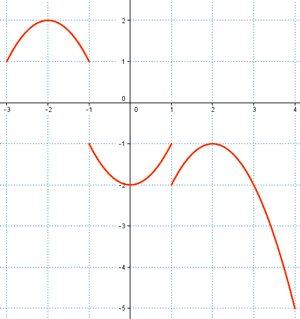
c)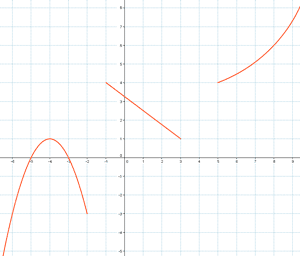
d)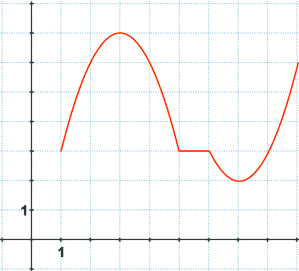
3) Estudia el crecimiento, el decrecimiento, los máximos y los mínimos de las siguientes funciones.
a)
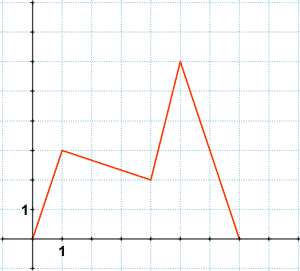
b)

c)
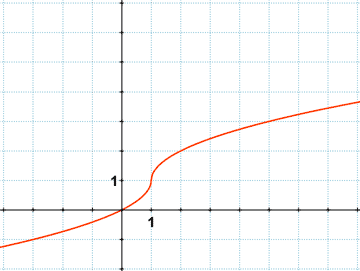
d)

4) Realiza un estudio completo de las siguientes funciones.
a)
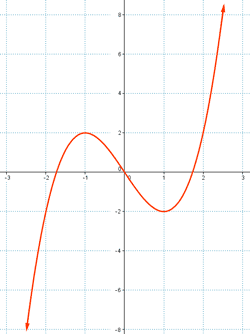
b)
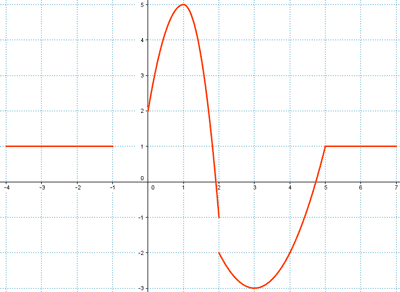
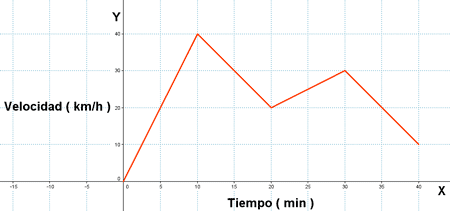
5) La velocidad de un ciclista varía según se indica en la gráfica. Realiza un estudio completo de la función :
a) Dominio y continuidad.
b) Tramos donde la función crece o decrece.
c) Máximos y/o mínimos, absolutos o relativos.
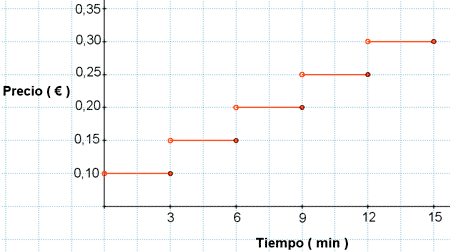
6) La gráfica siguiente muestra el precio de una llamada telefónica con un determinado contrato.
a) Identifica las variables. ¿Es una función?
b) Averigua si es una función creciente o decreciente.
c) ¿Tiene máximos y mínimos?
d) ¿Cuánto costará una llamada de 7 minutos¿ ¿Y una de 4 minutos? ¿Y otra de 11 minutos?
e) Si sólo podemos gastar 30 céntimos, ¿cuánto tiempo podré hablar?
f) ¿Es una función continua?
1) Estudia el dominio y recorrido de las siguientes funciones.
a)

b)
c)

d)

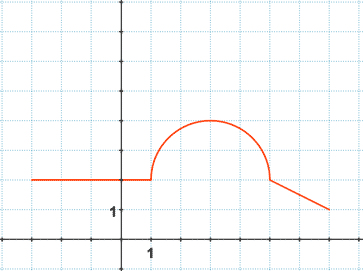
a)
Dominio : Dom f(x) → desde x = - 3 hasta x = 7
Recorrido : Rec f(x) → desde y = 1 hasta y = 4
b)
Dominio : Dom f(x) → desde x = -2 hasta x = 2
Recorrido : Rec f(x) → desde y = 0 hasta y = 4
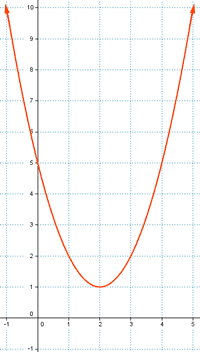
c)
Dominio : Dom f(x) = Q ( Todos los números racionales )
Recorrido :
Rec f(x) → A partir de y = 1
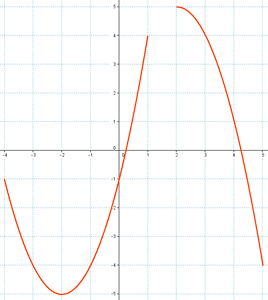
d)
Dominio : Dom f(x) → desde x = - 4 hasta x = 6
Recorrido : Rec f(x) → desde y = - 5 hasta y = 5
2) Estudia la continuidad o discontinuidad de las siguientes funciones.
a)
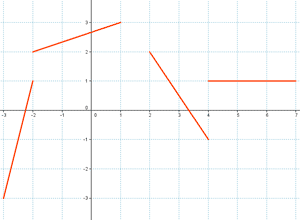
b)

c)
d)
a)
La función es discontinua : en x =
- 2 ; desde x = 1 hasta x = 2 ; en x = 4
b)
La función es discontinua : en x = - 1 y en x = 1
c)
La función es discontinua : desde x = - 2 hasta x = -1 ; desde x = 3 hasta x = 5
d)
La función es continua.
3) Estudia el crecimiento y decrecimiento de las siguientes funciones.
a)

b)

c)

d)

a)
La función es creciente desde x = 0 hasta x = 1 y desde x = 4 hasta x = 5
La función es decreciente desde x = 1 hasta x = 4 y desde x = 5 hasta x = 7
Tiene un máximo relativo en x = 1 y un máximo absoluto en x = 5
Tienen un mínimo relativo en x = 4
b)
La función es constante desde x = - 3 hasta x = 1
La función es creciente desde x = 1 hasta x = 3
La función es decreciente desde x = 3 hasta x = 7
Tiene un máximo absoluto en x = 3
c)
La función es creciente desde x = - ∞ hasta x = ∞
La función no tiene máximos o mínimos.
d)
La función es creciente desde x = 1 hasta x = 3 y desde x = 8 hasta x = ∞.
La función es decreciente desde x =
3 hasta x = 5 y desde x = 6 hasta x = 7
La función es constante desde x = 5 hasta x = 6
Tienen un máximo absoluto en x = 3
Tienen un mínimo absoluto en x =
7
4) Realiza un estudio completo de las siguientes funciones.
a)

b)

a)
Dominio : Dom f(x) = Q ( Todos los números racionales )
Recorrido : Rec f(x) = Q ( Todos los números racionales )
La función es continua.
La función es creciente : desde x = - ∞ hasta x = -1 y desde x = 1 hasta x = ∞
La función es decreciente : desde x = -1 hasta x = 1.
Tiene un máximo relativo en el punto ( - 1, 2 ) y un mínimo relativo en el punto ( 1, - 2 )
b)
Dominio : ´Dom f (x) = desde x = -4 hasta x = - 1 y desde x = 0 hasta x = 7
Recorrido : Rec f(x) = desde y = - 3 hasta y = 5
La función es discontinua desde : x = -1 hasta x = 2 y en el punto x = 2
La función es creciente : desde x = 0 hasta x = 1 y desde x = 3 hasta x = 5
La función es decreciente : desde x = 1 hasta x = 3
La función es constante : desde x = - 4 hasta x = 1
y desde x = 5 hasta x = 7
5) La velocidad de un ciclista varía según se indica en la gráfica. Realiza un estudio completo de la función :

a) Dominio y continuidad.
b) Tramos donde la función crece o decrece.
c) Máximos y/o mínimos, absolutos o relativos.
a)
Dominio : Dom f(x) = desde x = 0 hasta x = 40
La función es continua.
b)
Crece desde x = 0 hasta x = 10 y desde x = 20 hasta x = 30
Decrece desde x = 10 hasta x = 20 y dese x = 30 hasta x = 40
c)
Tiene un mínimo absoluto en ( 20, 20 )
Tiene un máximo absoluto en ( 10, 40 ) y un mínimo relativo en ( 30, 30 )
6) La gráfica siguiente muestra el precio de una llamada telefónica con un determinado contrato.

a) Identifica las variables. ¿Es una función?
b) Averigua si es una función creciente o decreciente.
c) ¿Tiene máximos y mínimos?
d) ¿Cuánto costará una llamada de 7 minutos¿ ¿Y una de 4 minutos? ¿Y otra de 11 minutos?
e) Si sólo podemos gastar 30 céntimos, ¿cuánto tiempo podré hablar?
f) ¿Es una función continua?
a)
Las variables son el tiempo de la llamada y el precio de dicha llamada.
b)
La función es creciente, ya que cuanto mayor tiempo dure la llamada, mayor es el precio que tendremos que pagar.
c)
No, la función no tiene máximos o mínimos, ya que no hay ningún punto de la misma donde pase de ser creciente a decreciente o viceversa.
d)
Una llamada de 7 minutos costará 0,20 euros, ya que los 7 minutos están entre 6 y 9 minutos.
Una llamada de 4 minutos costrá 0,15 euros, ya que los 4 minutos están entre 3 y 6 minutos.
Una llamada de 11 minutos tendrá un precio de 0,30 euros, ya que los 11 minutos se encuentran entre 12 y 15 minutos.
e)
Al tener sólo 0,30 euros nuestra llamada tendrá una duración máxima de 15 minutos.
f)
No, se trata de una fracción escalonada.


 INICIO
INICIO