Medidas de posición: cuartiles, deciles y percentiles
Las medidas de posición son valores de la variable que informan del lugar que ocupa un dato dentro
del conjunto ordenado de valores.
Los cuartiles Q1 , Q2 y Q3 son tres valores de la variable estadística que divide en cuatro partes el número de datos. Es decir, que cada tramo será el 25% de los datos recogidos en el estudio.
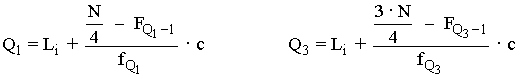
La mediana coincide con el cuartil dos (Me = Q2)
- Cuartil inferior: Q1 es un valor de la variable que deja por debajo de él al 25% de la población
y por encima al 75%. - Cuartil superior: Q3 es un valor de la variable que deja por debajo de él al 75% de la población
y por encima al 25%.
El rango intercuartílico (r)es la diferencia entre el tercero y el primer cuartil.
r = Q3 - Q1
Ejemplo 1:
En la distribución : 1, 1, 2, 2, 3, 4, 4, 4, 5, 6, 6, 6, 8, 8, 9, 10 .
Hallar cuartiles y mediana.
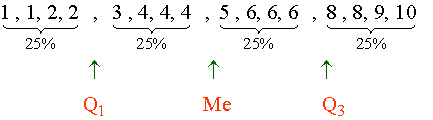
estos parámetros toman los valores siguientes: Q1= 2,5 ; Me = 4,5 ; Q3 = 7
el rango intercuartílico será: r = 7-2,5 = 4,5
Los deciles D1 , D2 , D3 , ... , D9 son nueve valores de la variable estadística que divide en diez partes el número de datos. Es decir, que cada tramo será el 10% de los datos recogidos en el estudio.
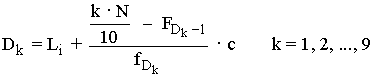
Los percentiles o centiles Pk , son 99 valores de la variable estadística que dividen en 100 partes el número de datos.
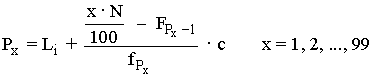


Cálculo de medidas de posición
Para calcular las medidas de posición la variable debe ser cuantitativa y además se trabaja con
las frecuencias acumuladas. Si la variable es continua, tomamos como valor la marca de clase.
Diagramas de caja o caja y bigotes
Los puntos que separan los cuatro trozos son los cuartiles y la mediana.
Ejemplo 2:
Dadas las notas de un test con una puntuación del 0 al 6 de 128 alumnos.
Representar, mediante un diagrama de caja, la siguiente distribución:
| 0 | 15 | 15 |
| 1 | 20 | 35 |
| 2 | 44 | 79 |
| 3 | 27 | 106 |
| 4 | 13 | 119 |
| 5 | 7 | 126 |
| 6 | 2 | 128 |
| Sumatorio | 128 |

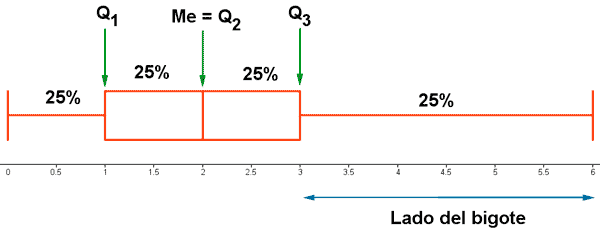
Las notas presentan una dispersión grande puesto que el 50% sólo han respondido 2 preguntas.
Además de que del 3 al 6 hay tan sólo un 25% de los alumnos.
Ejemplo 3:
Se ha pasado un test de 79 preguntas a 600 personas. El número de respuestas
correctas se refleja en la siguiente tabla :
| Respuesta | [ 0, 10 ) | [ 10, 20 ) | [ 20, 30 ) | [ 30, 40 ) | [ 40, 50 ) | [ 50, 60 ) | [ 60, 70 ) | [ 70, 80 ) |
|---|---|---|---|---|---|---|---|---|
| Nº de peronas | 40 | 60 | 75 | 90 | 105 | 85 | 80 | 65 |
Calcular los cuartiles, la mediana, el rango intercuartílico, el decil 2, el decil 8 ,
el percentil 48 y el
percentil 67.
| Intervalos | xi | fi | Fi | xi2 | fi·xi | fi·xi2 |
|---|---|---|---|---|---|---|
| [ 0, 10 ) | 5 | 40 | 40 | 25 | 200 | 1000 |
| [ 10, 20 ) | 15 | 60 | 100 | 225 | 900 | 13500 |
| [ 20, 30 ) | 25 | 75 | 175 | 625 | 1875 | 46875 |
| [ 30, 40 ) | 35 | 90 | 265 | 1225 | 3150 | 110250 |
| [ 40, 50 ) | 45 | 105 | 370 | 2025 | 4725 | 212625 |
| [ 50, 60 ) | 55 | 85 | 455 | 3025 | 4675 | 257125 |
| [ 60, 70 ) | 65 | 80 | 535 | 4225 | 5200 | 338000 |
| [ 70, 80 ) | 75 | 65 | 600 | 5625 | 4875 | 365625 |
| Sumatorios | 25600 | 1345000 | ||||

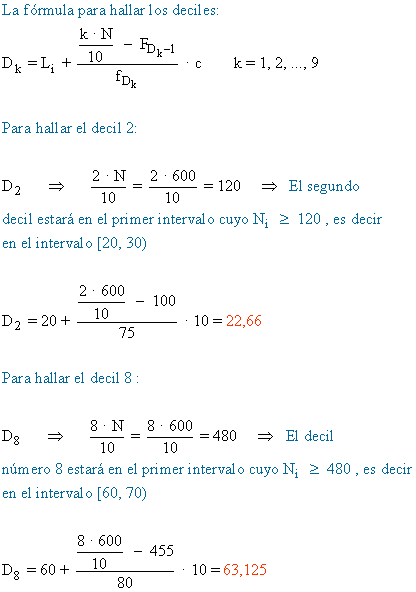



 INICIO
INICIO

