Problemas resueltos de estudio conjunto de la media y la varianza
1) Los jugadores de un determinado equipo de baloncesto se clasifican por alturas según la tabla siguiente:
Altura
[1,70 , 1,75)
[1,75 , 1,80)
[1,80 , 1,85)
[1,85 , 1,90)
[1,90 , 1,95)
[1,95 , 2,00)
Nº de jugadores
1
3
4
8
5
2
| Altura | [1,70 , 1,75) | [1,75 , 1,80) | [1,80 , 1,85) | [1,85 , 1,90) | [1,90 , 1,95) | [1,95 , 2,00) |
|---|---|---|---|---|---|---|
| Nº de jugadores | 1 | 3 | 4 | 8 | 5 | 2 |
¿Cuántos valores hay en los intervalos (
) , (
) y (
)? Estudia la concentración de los datos.
2) En un grupo de alumnos, se ha efectuado un test de habilidad mental obteniéndose:
Puntuaciones
[12, 23)
[23, 34)
[34, 45)
[45, 56)
[56, 67)
[67, 78)
Nº de alumnos
12
27
24
36
15
12
| Puntuaciones | [12, 23) | [23, 34) | [34, 45) | [45, 56) | [56, 67) | [67, 78) |
|---|---|---|---|---|---|---|
| Nº de alumnos | 12 | 27 | 24 | 36 | 15 | 12 |
Se pide:
a) Porcentaje de alumnos con una puntuación que pertenezca al intervalo ().
b) Calcular la mediana.3) Completar los datos que faltan en la siguiente tabla estadística, donde hi, Fi y fi, representan, respectivamente, la frecuencia relativa, absoluta acumulada y absoluta.
Calcular además: media, moda y mediana de la distribución.
| 1 | 4 | 0,08 | |
| 2 | 4 | ||
| 3 | 16 | 0,16 | |
| 4 | 7 | 0,14 | |
| 5 | 5 | 28 | |
| 6 | 38 | ||
| 7 | 7 | 45 | |
| 8 |
4) Al estudiar la distribución de la edad en una población se obtuvieron los resultados siguientes:
| Edad (en años) | (0,20] | (20,40] | (40,60] | (60,80] |
|---|---|---|---|---|
| Nº de individuos | 15 | ? | 15 | 16 |
Como se ve, se ha extraviado el dato correspondiente al intervalo (20, 40].
a) ¿Cuál sería el valor de ese dato si la edad media fuera de 35 años?
b) ¿Cuál sería el valor de ese dato si la edad mediana fuera de 35 años?
c) ¿Cuál sería la desviación típica si el dato fuera 16?
5)
Considérense los siguientes datos: 9, 11, 7, 12, 11. Se pide:
a) Calcular su media, varianza y desviación típica.
b) Considérese también el conjunto de datos obtenido sumando 20 a cada uno de los datos iniciales. Razonar, cuál de los dos conjuntos está más disperso respecto de su media.
b) Considérese también el conjunto de datos obtenido sumando 20 a cada uno de los datos iniciales. Razonar, cuál de los dos conjuntos está más disperso respecto de su media.
6) Las edades, en años, de los asistentes a cierto curso fueron :
37, 35, 38, 36, 37, 40, 38, 25, 38
a) ¿Cuál es la edad media de los asistentes?
b) La varianza del conjunto de datos anterior es 19. Las mismas personas asistirán a otro curso dentro de 2 años. Obtener razonadamente la media y la varianza del nuevo conjunto de datos a partir de las correspondientes al conjunto de datos inicial.7) Considérense los siguientes datos: 9, 11, 7, 12, 11. Se pide:
a) Calcular su media, varianza y desviación típica.
b) Considérese también el conjunto de datos obtenido multiplicando por 5 a cada uno de los datos iniciales. Razonar, cuál de los dos conjuntos está más disperso respecto de su media.8) En una clase hay 20 alumnos y 15 alumnas. El peso medio de los 20 alumnos es de 64,7 kg y el de las 15 alumnas es de 57,3 kg. Supongamos que las desviaciones típicas de los dos grupos son, respectivamente, 4,2 kg y 5,7 kg. El peso de Luis es de 71 kg y el de Laura es de 62 kg. ¿Cuál de ellos puede, dentro del grupo de alumnos de su sexo, considerarse más grueso?
9) Se ha realizado una prueba, en una determinada asignatura, a dos grupos de alumnos, el grupo A y el B. De la información obtenida se han hecho los siguientes cálculos :

Los alumnos 1 y 2 han obtenido los siguientes resultados :
¿Cuál de los alumnos puede considerarse mejor?
10) Un profesor ha realizado dos test a un grupo de 40 alumnos, obteniendo los siguientes resultados :
- Para el primer test, la media es 6 y la desviación típica 1,5.
- Para el segundo test la media es 4 y la desviación típica 0,5.
Un alumno obtiene un 6 en el primero y un 5 en el segundo. En relación con el grupo, ¿en cuál de los test obtuvo mejor puntuación?11) Una persona A mide 1,75 metros y reside en una ciudad donde la estatura media es de 1,60 metros y su desviación típica es de 20 centímetros. Otra persona B mide 1,80 metros y vive en una ciudad donde la estatura media es de 1,70 metros y la desviación típica es de 15 centímetros.
¿Cuál de las dos será más alta respecto a sus conciudadanos?
12) En un grupo de sociología se han obtenido las siguientes puntuaciones en un test de habilidad mental :
50, 23, 45, 36, 56, 34, 56, 67, 45, 34, 23, 45, 23, 67, 54, 21,
34, 43, 12, 78, 36, 49, 53, 27, 66, 31, 45, 22, 33, 44, 48, 53,
57, 77, 31, 23, 47, 52, 33, 37, 64, 21.
Comprobar si en el intervalose encuentra aproximadamente el 68 % de los datos.
1) Los jugadores de un determinado equipo de baloncesto se clasifican por alturas según la tabla siguiente:
Altura
[1,70 , 1,75)
[1,75 , 1,80)
[1,80 , 1,85)
[1,85 , 1,90)
[1,90 , 1,95)
[1,95 , 2,00)
Nº de jugadores
1
3
4
8
5
2
| Altura | [1,70 , 1,75) | [1,75 , 1,80) | [1,80 , 1,85) | [1,85 , 1,90) | [1,90 , 1,95) | [1,95 , 2,00) |
|---|---|---|---|---|---|---|
| Nº de jugadores | 1 | 3 | 4 | 8 | 5 | 2 |
¿Cuántos valores hay en los intervalos (
) , (
) y (
)? Estudia la concentración de los datos.
| Altura | |||||
|---|---|---|---|---|---|
| [1,70 , 1,75) | 1,725 | 1 | 2,976 | 1,725 | 2,976 |
| [1,75 , 1,80) | 1,775 | 3 | 3,151 | 5,325 | 9,453 |
| [1,80 , 1,85) | 1,825 | 4 | 3,331 | 7,3 | 13,324 |
| [1,85 , 1,90) | 1,875 | 8 | 3,516 | 15,0 | 28,128 |
| [1,90 , 1,95) | 1,925 | 5 | 3,706 | 9,625 | 18,53 |
| [1,95 , 2,00) | 1,975 | 2 | 3,901 | 3,95 | 7,802 |
| Sumatorio | 11,1 | 23 | 20,578 | 42,925 | 80,213 |

2) En un grupo de alumnos, se ha efectuado un test de habilidad mental obteniéndose:
Puntuaciones
[12, 23)
[23, 34)
[34, 45)
[45, 56)
[56, 67)
[67, 78)
Nº de alumnos
12
27
24
36
15
12
| Puntuaciones | [12, 23) | [23, 34) | [34, 45) | [45, 56) | [56, 67) | [67, 78) |
|---|---|---|---|---|---|---|
| Nº de alumnos | 12 | 27 | 24 | 36 | 15 | 12 |
Se pide:
a) Porcentaje de alumnos con una puntuación que pertenezca al intervalo ().
b) Calcular la mediana.
| Intervalos | |||||
|---|---|---|---|---|---|
| [12, 23) | 17,5 | 12 | 12 | 210 | 3675 |
| [23, 34) | 28,5 | 27 | 39 | 769,5 | 21930,75 |
| [34, 45) | 39,5 | 24 | 63 | 948 | 37446 |
| [45, 56) | 50,5 | 36 | 99 | 1818 | 91809 |
| [56, 67) | 61,5 | 15 | 114 | 922,5 | 56733,75 |
| [67, 78) | 72,5 | 12 | 126 | 870 | 63075 |
| Sumatorio: | 126 | 5538 | 274669,5 | ||

3) Completar los datos que faltan en la siguiente tabla estadística, donde hi, Fi y fi, representan, respectivamente, la frecuencia relativa, absoluta acumulada y absoluta.
Calcular además: media, moda y mediana de la distribución.
| 1 | 4 | 0,08 | |
| 2 | 4 | ||
| 3 | 16 | 0,16 | |
| 4 | 7 | 0,14 | |
| 5 | 5 | 28 | |
| 6 | 38 | ||
| 7 | 7 | 45 | |
| 8 |

| 1 | 4 | 4 | 0,08 |
| 2 | 4 | 8 | 0,08 |
| 3 | 8 | 16 | 0,16 |
| 4 | 7 | 23 | 0,14 |
| 5 | 5 | 28 | 0,1 |
| 6 | 10 | 38 | 0,2 |
| 7 | 7 | 45 | 0,14 |
| 8 | 5 | 50 | 0,1 |

4) Al estudiar la distribución de la edad en una población se obtuvieron los resultados siguientes:
| Edad (en años) | (0,20] | (20,40] | (40,60] | (60,80] |
|---|---|---|---|---|
| Nº de individuos | 15 | ? | 15 | 16 |
Como se ve, se ha extraviado el dato correspondiente al intervalo (20, 40].
a) ¿Cuál sería el valor de ese dato si la edad media fuera de 35 años?
b) ¿Cuál sería el valor de ese dato si la edad mediana fuera de 35 años?
c) ¿Cuál sería la desviación típica si el dato fuera 16?
| Marcas de clase |
|||
|---|---|---|---|
| (0 , 20] | 10 | 15 | 150 |
| (20, 40] | 30 | a | 30 · a |
| (40, 60] | 50 | 15 | 750 |
| (60, 80] | 70 | 16 | 1120 |
| Sumatorio | 46+a | 2020+30·a | |
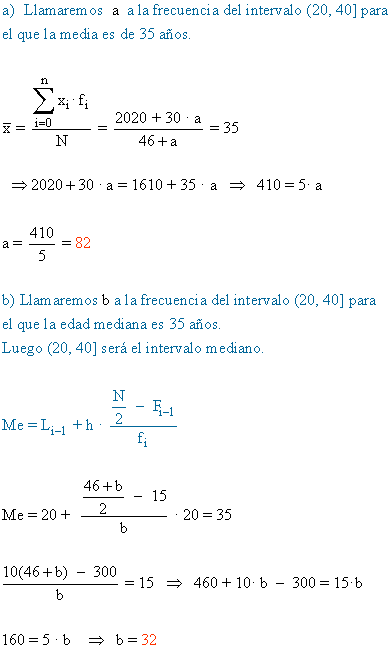
| 10 | 15 | 100 | 150 | 1 000 |
| 30 | 16 | 900 | 480 | 27 000 |
| 50 | 15 | 2 500 | 750 | 125 000 |
| 70 | 16 | 4 900 | 1120 | 343 000 |
| 62 | 2 500 | 496 000 |
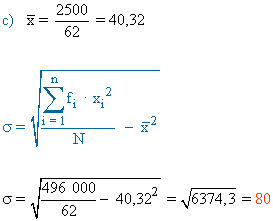
5) Considérense los siguientes datos: 9, 11, 7, 12, 11. Se pide:
a) Calcular su media, varianza y desviación típica.
b) Considérese también el conjunto de datos obtenido sumando 20 a cada uno de los datos iniciales. Razonar, cuál de los dos conjuntos está más disperso respecto de su media.

6) Las edades, en años, de los asistentes a cierto curso fueron :
37, 35, 38, 36, 37, 40, 38, 25, 38
a) ¿Cuál es la edad media de los asistentes?
b) La varianza del conjunto de datos anterior es 19. Las mismas personas asistirán a otro curso dentro de 2 años. Obtener razonadamente la media y la varianza del nuevo conjunto de datos a partir de las correspondientes al conjunto de datos inicial.
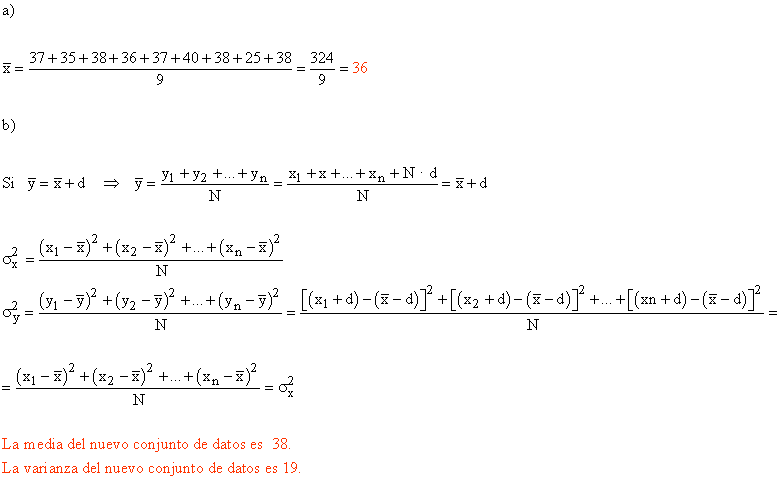
7) Considérense los siguientes datos: 9, 11, 7, 12, 11. Se pide:
a) Calcular su media, varianza y desviación típica.
b) Considérese también el conjunto de datos obtenido multiplicando por 5 a cada uno de los datos iniciales. Razonar, cuál de los dos conjuntos está más disperso respecto de su media.

8) En una clase hay 20 alumnos y 15 alumnas. El peso medio de los 20 alumnos es de 64,7 kg y el de las 15 alumnas es de 57,3 kg. Supongamos que las desviaciones típicas de los dos grupos son, respectivamente, 4,2 kg y 5,7 kg. El peso de Luis es de 71 kg y el de Laura es de 62 kg. ¿Cuál de ellos puede, dentro del grupo de alumnos de su sexo, considerarse más grueso?

9) Se ha realizado una prueba, en una determinada asignatura, a dos grupos de alumnos, el grupo A y el B. De la información obtenida se han hecho los siguientes cálculos :

Los alumnos 1 y 2 han obtenido los siguientes resultados :
¿Cuál de los alumnos puede considerarse mejor?

10) Un profesor ha realizado dos test a un grupo de 40 alumnos, obteniendo los siguientes resultados :
- Para el primer test, la media es 6 y la desviación típica 1,5.
- Para el segundo test la media es 4 y la desviación típica 0,5.
Un alumno obtiene un 6 en el primero y un 5 en el segundo. En relación con el grupo, ¿en cuál de los test obtuvo mejor puntuación?
Tenemos que hallar los valores tipificados de cada una de las notas en sus respectivos test.

11) Una persona A mide 1,75 metros y reside en una ciudad donde la estatura media es de 1,60 metros y su desviación típica es de 20 centímetros. Otra persona B mide 1,80 metros y vive en una ciudad donde la estatura media es de 1,70 metros y la desviación típica es de 15 centímetros.
¿Cuál de las dos será más alta respecto a sus conciudadanos?
Vamos a calcular la variable tipificada de cada una de las personas respecto a sus conciudadanos.

12) En un grupo de sociología se han obtenido las siguientes puntuaciones en un test de habilidad mental :
50, 23, 45, 36, 56, 34, 56, 67, 45, 34, 23, 45, 23, 67, 54, 21,
34, 43, 12, 78, 36, 49, 53, 27, 66, 31, 45, 22, 33, 44, 48, 53,
57, 77, 31, 23, 47, 52, 33, 37, 64, 21.
Comprobar si en el intervalose encuentra aproximadamente el 68 % de los datos.
Los valores extremos son 12 y 78, así que agruparemos los valores como figura en la tabla de distribución siguiente :
| li | xi | fi | Fi | fi · xi | xi2 | fi · xi2 |
|---|---|---|---|---|---|---|
| ( 10, 20 ] | 15 | 1 | 1 | 15 | 225 | 225 |
| ( 20, 30 ] | 25 | 8 | 9 | 200 | 625 | 5000 |
| ( 30, 40 ] | 35 | 10 | 19 | 350 | 1225 | 12250 |
| ( 40, 50 ] | 45 | 9 | 28 | 405 | 2025 | 18225 |
| ( 50, 60 ] | 55 | 8 | 36 | 440 | 3025 | 24200 |
| ( 60, 70 ] | 65 | 4 | 40 | 260 | 4225 | 16900 |
| ( 70, 80 ] | 75 | 2 | 42 | 150 | 5625 | 11250 |
| Sumatorios | 42 | 1820 | 88050 | |||



 INICIO
INICIO