Medidas de centralización
Media aritmética
En caso que los datos estén agrupados en intervalos, se toman como valores las marcas de clase.
Su cálculo se realiza atendiendo a cómo se presenten los datos:
Para datos sin frecuencias:
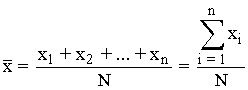
El símbolo ![]() se lee sumatorio y significa suma de todos los datos. Mientras que
se lee sumatorio y significa suma de todos los datos. Mientras que ![]() indica la
indica la
suma desde el primero hasta el n-ésimo dato.
Ejemplo 1:
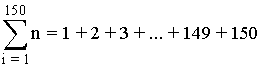
Para datos con frecuencias:
En caso de que los datos esten agrupados en intervalos, se toman como valores las marcas de clase:
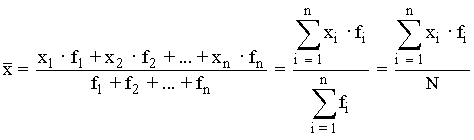
Consideraciones sobre la media aritmética:
- Es el parámetro de centralización más usado.
- No siempre podemos calcularla, y aún cuando podamos hacerlo, hay casos en los que carece
de significado. En esos casos se usan otras medidas de dispersión. - Si se suma una constante a todos los valores de la variable, la media aritmética aumenta en
el mismo valor. - Si multiplicamos todos los valores de la variable por el mismo número, la media queda multiplicada
por dicho número.
Con datos ponderados:
La media ponderada se calcula cuando los valores de la variable no tienen el mismo peso. La fórmula es análoga a la anterior cambiando frecuencias fi por pesos pi, y en el denominador N por la suma de todos los pesos pi:
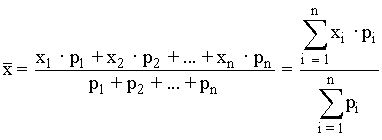
Ejemplo 2:
Las notas de matemáticas de los alumnos de una clase son las siguientes :
3, 3, 7, 6, 8, 7, 6, 7, 5, 5, 4, 5, 4, 6, 4,
5, 7, 8, 5, 4, 5, 6, 7, 9, 6, 10, 3, 2, 6, 6
Obtén la tabla de frecuencias, la media aritmética y la media ponderada.
| xi | fi | hi | pi | Fi | Hi | Pi |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0,033 | 3,3 | 1 | 0,033 | 3,3 |
| 3 | 3 | 0,1 | 10 | 4 | 0,133 | 13,3 |
| 4 | 4 | 0,133 | 13,3 | 8 | 0,266 | 26,6 |
| 5 | 6 | 0,2 | 20 | 14 | 0,466 | 46,6 |
| 6 | 7 | 0,234 | 23,4 | 21 | 0,7 | 70 |
| 7 | 5 | 0,167 | 16,7 | 26 | 0,867 | 86,7 |
| 8 | 2 | 0,067 | 6,7 | 28 | 0,934 | 93,4 |
| 9 | 1 | 0,033 | 3,3 | 29 | 0,967 | 96,7 |
| 10 | 1 | 0,033 | 3,3 | 30 | 1 | 100 |
| Sumatorio | N = 30 | 1 | 100 | |||
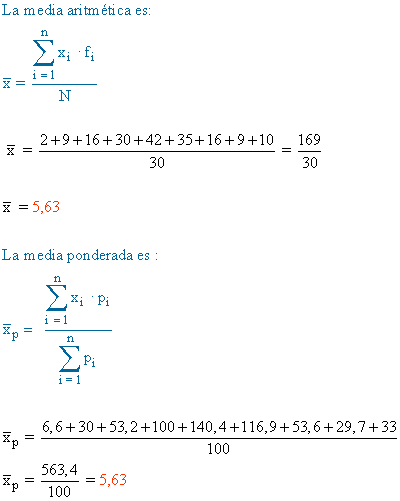
Ejemplo 2:
Las calificaciones en una clase de lenguaje tienen cuatro componentes,
con los pesos
indicados: lectura (25 %), lectura comprensiva (45 %) ,
ortografía (20 %) y
elaboración de trabajo (10%).
Si un alumno fue calificado respectivamente con un :
6, 5, 7 y 9.
¿Cuál será su nota media? Halla su nota media si todos los componentes
tuvieran el mismo peso. ¿Cómo conseguiría sacar mayor nota?
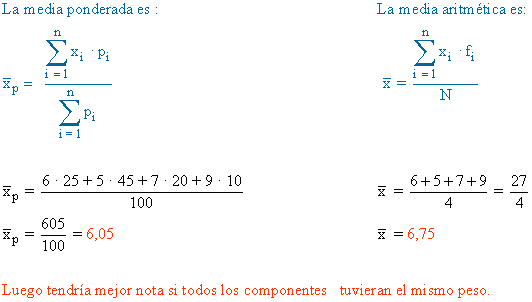


 INICIO
INICIO

