Medidas de dispersión
Varianza
Varianza de una variable estadística es la media aritmética de los cuadrados de las desviaciones de todos los datos o marcas de clase respecto de la media.
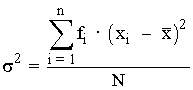
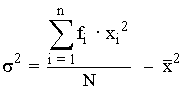
Desviación típica
La desviación típica de una variable estadística es la raíz cuadrada positiva de la varianza.
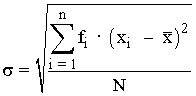
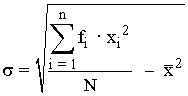
- La desviación típica es el parámetro de dispersión más utilizado.
- Si se suma una constante a todos los valores de la variable, la desviación típica no varía.
- Si se multiplican todos los valores de la variable por un mismo número, la desviación típica
queda multiplicada por el mismo número.
Coeficiente de variación o coeficiente de variación de Pearson
![]()
El CV se interpreta como el número de veces que la desviación típica contiene a la media.
- El valor del CV se multiplica por 100 para trabajar en porcentajes.
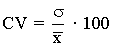
Diremos que la dispersión es elevada cuando el CV sea superior al 30%. - Dados dos conjuntos de datos, aquel que tenga un coeficiente de vaciarión mayor es el más
disperso, el más heterogéneo. - El valor de la CV no depende de la unidad de medida utilizada, luego es adimensional, lo que
significa que podemos comparar variables expresadas en magnitudes diferentes o en la misma
magnitud pero con destintas medias.
Ejemplo 1:
Las notas no agrupadas correspondientes a un examen que ha sido realizado por los alumnos de tres grupos diferentes 1, 2 y 3, con 20 alumnos cada grupo nos da como resultado los tres histogramas siguientes:
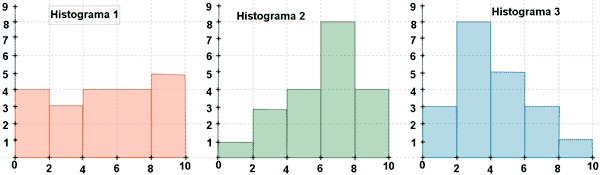
Como resultado se han obtenido la media y la desviación típica de cada una de ellas.
¿Cuál de ellos tiene mayor dispersión?
| H-1 | H-2 | H-3 | |
|---|---|---|---|
| Media | 5,3 | 6,1 | 4,1 |
| Desviación típica | 2,925 | 2,23 | 2,14 |

Ejemplo 2:
La tabla muestra las temperaturas en Londres a lo largo de cien días. Halla las medidas
de centralización, de posición y de dispersión.
| Temperatura | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|
| Nº de días | 10 | 17 | 40 | 22 | 5 | 6 |
| 15 | 10 | 10 | 150 | 2250 | 21,3 |
| 16 | 17 | 27 | 272 | 4352 | 19,21 |
| 17 | 40 | 67 | 680 | 11560 | 5,2 |
| 18 | 22 | 89 | 396 | 7128 | 19,14 |
| 19 | 5 | 94 | 95 | 1805 | 9,35 |
| 20 | 6 | 100 | 120 | 2400 | 17,22 |
| Sumatorio: | 100 | 1713 | 29495 | 91,42 |

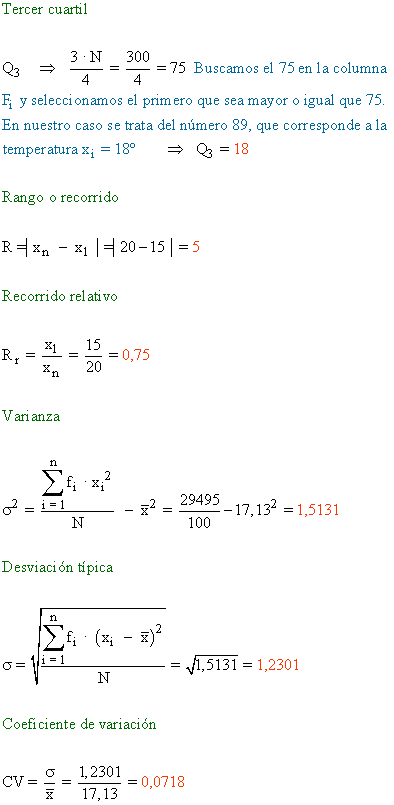
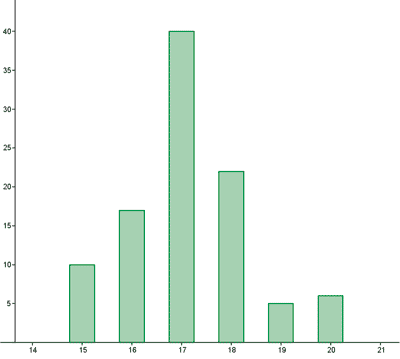
Ejemplo 3:
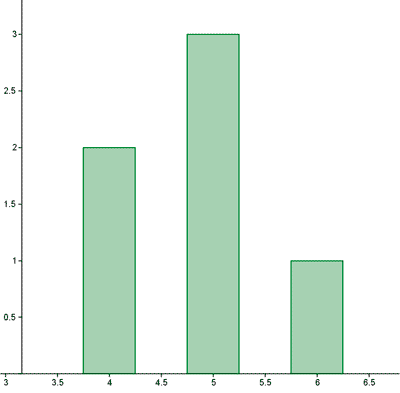
Calcula las medidas de dispersión de las notas de 6 alumnos. Las notas son: 4, 4, 5, 5, 5, 6
| 4 | 2 | 0,83 | 0,6889 |
| 5 | 3 | 0,17 | 0,0289 |
| 6 | 1 | 1,17 | 1,3689 |
| Sumatorio | 6 | 2,0867 |
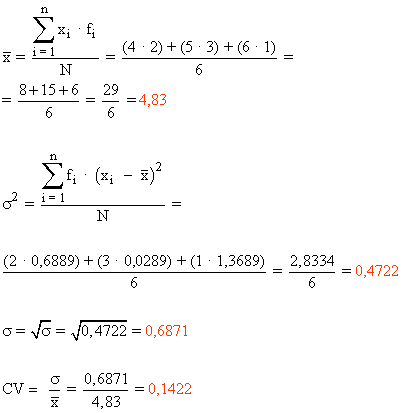


 INICIO
INICIO

