Mediana
Cálculo de la mediana con tablas de frecuencia para variables estadísticas discretas
Si el número de datos es impar la mediana coincide con el dato que ocupa el lugar central. Y si es
par, es la media aritmética de los dos datos que ocupan los lugares centrales.

Cálculo de la mediana para variables estadísticas continuas
En caso de que los datos estén agrupados intervalos, se define la clase mediana o intervalo mediano
como el intervalo
que contiene la mediana.
Si el número de datos es impar, la clase medianal es el intervalo que contiene al dato central. Y si es
par, los datos pertenecen a un mismo intervalo, la clase medianal es dicho intervalo.
Se puede determinar con la siguiente fórmula:
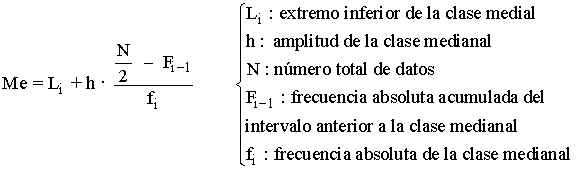
Ejemplo 1:
Calcula la mediana de los siguientes datos :
a) 7, 7, 5, 3, 9, 8, 10
b) 8, 2, 5, 4, 6, 6, 6, 7
c) 2, 4, 3, 2, 3, 5, 8, 7
d) 4, 4, 4, 6, 7, 6, 6, 5, 5, 5, 8, 7, 9
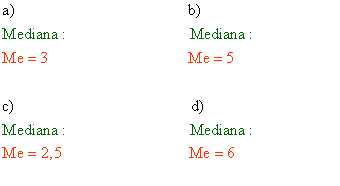
Ejemplo 2:
Considérese la tabla de frecuencias agrupadas:
| Intervalo | [3,5 , 6,5) | [6,5 , 9,5) | [9,5 , 12,5) | [12,5 , 15,5) | [15,5 , 18,5) |
|---|---|---|---|---|---|
| Frecuencias | 3 | 5 | 9 | 6 | 2 |
Hallar la mediana de forma gráfica y de forma analítica.
| Intervalo | ||
|---|---|---|
| [3,5 , 6,5) | 3 | 3 |
| [6,5 , 9,5) | 5 | 8 |
| [9,5 , 12,5) | 9 | 17 |
| [12,5 , 15,5) | 6 | 23 |
| [15,5 , 18,5) | 2 | 25 |
| Sumatorio: | 25 |
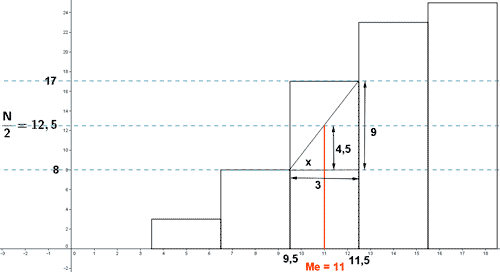
Dibujamos el histograma de frecuencias absolutas acumuladas (Fi) y para hallar la mediana utilizamos la semejanza de triángulos.
Primero: se calcula N/2 = 12,5. Como no coincide con ninguna frecuencia absoluta acumulada, la mediana NO es el extremo superior del intervalo correspondiente a N/2 .
Por tanto dibujamos el histograma utilizando las frecuencias abosolutas y resolvemos por semejanza de triángulos.
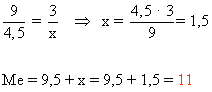

Ejemplo 3:
Se ha pasado un test de 79 preguntas a 600 personas. El número de respuestas
correctas se refleja en la siguiente tabla :
| Respuesta | [ 0, 10 ) | [ 10, 20 ) | [ 20, 30 ) | [ 30, 40 ) | [ 40, 50 ) | [ 50, 60 ) | [ 60, 70 ) | [ 70, 80 ) |
|---|---|---|---|---|---|---|---|---|
| Nº de peronas | 40 | 60 | 75 | 90 | 105 | 85 | 80 | 65 |
Calcula la mediana.
| Intervalos | xi | fi | Fi | xi2 | fi·xi | fi·xi2 |
|---|---|---|---|---|---|---|
| [ 0, 10 ) | 5 | 40 | 40 | 25 | 200 | 1000 |
| [ 10, 20 ) | 15 | 60 | 100 | 225 | 900 | 13500 |
| [ 20, 30 ) | 25 | 75 | 175 | 625 | 1875 | 46875 |
| [ 30, 40 ) | 35 | 90 | 265 | 1225 | 3150 | 110250 |
| [ 40, 50 ) | 45 | 105 | 370 | 2025 | 4725 | 212625 |
| [ 50, 60 ) | 55 | 85 | 455 | 3025 | 4675 | 257125 |
| [ 60, 70 ) | 65 | 80 | 535 | 4225 | 5200 | 338000 |
| [ 70, 80 ) | 75 | 65 | 600 | 5625 | 4875 | 365625 |
| Sumatorios | 25600 | 1345000 | ||||



 INICIO
INICIO

