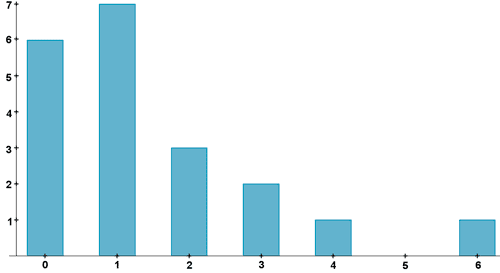Relaciones entre la media, la mediana y la moda
En una distribución con una sola moda:
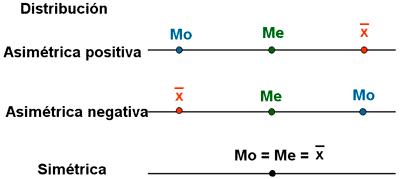
Si la distribución es asimétrica positiva, la media es superior a la mediana y ésta superior a la moda.
Si la distribución es asimétrica negativa, la media es inferior a la mediana y ésta inferior a la moda.
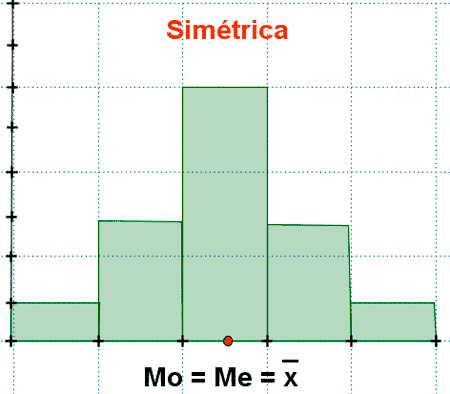
Si la distribución es simétrica, la media, la mediana y la moda coinciden.
Ejemplo 1:
Un médico atendió en 200 días las siguientes urgencias:
1, 3, 1, 1, 0, 1, 0, 2, 2, 0, 0, 1, 1, 2, 0, 6, 3, 1, 4, 0
a) Resumir los datos en una tabla que muestre frecuencias absolutas y porcentajes, y dibujar el correspondiente diagrama de barras.
b) Calcular la media, la mediana y la moda del conjunto de datos. ¿Es simétrica la distribución anterior?a)
0 6 0,30 30 1 7 0,35 35 2 3 0,15 15 3 2 0,10 10 4 1 0,05 5 6 1 0,05 5 Sumatorio: 20 1 100
b)
Ejemplo 2:
Una oficina bancaria ha tabulado las cantidades de dinero que retirarán 100 clientes en un determinado día en un cajero automático:
Euros (€) nº de clientes [0, 20) 33 [20, 40) 27 [40, 60) 19 [60, 80) 14 [80, 100) 7 Hallar:
a) Cantidad media de dinero retirado por cada cliente y desviación típica.
b) La mediana. Interpretar el resultado.a)
Intervalos [0, 20) 10 33 330 100 3300 33 [20, 40) 30 27 810 900 24300 60 [40, 60) 50 19 950 2500 47500 79 [60, 80) 70 14 980 4900 68600 93 [80, 100) 90 7 630 8100 56700 100 Sumatorio: 100 3700 200400

b)


 INICIO
INICIO