Raíces de números complejos en forma polar
Raíz enésima de un número complejo
Para hallar las raíces enésimas de un número complejo, se hace la raíz enésima del módulo y se divide el argumento entre el índice (n). Un número complejo distinto de cero tiene tantas raíces complejas como indica el índice:
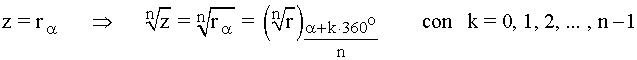
Ejemplos:
1) Halla las raíces quintas del siguiente número complejo: z = 32 i
En primer lugar pasamos el número complejo z a forma polar:
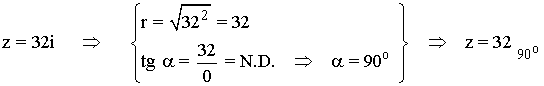
Sabemos que la tangente de un ángulo no está definida en 90o y 270o .
Como el afijo de z es (0, 32) el ángulo del número complejo es 90o .
A continuación aplicamos la fórmula para encontrar las 5 raíces quintas de z:
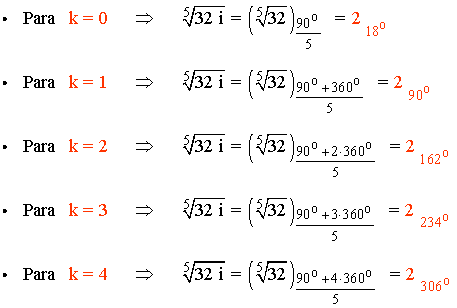
2) Calcula:
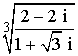
En primer lugar calculamos la forma polar del radicando:
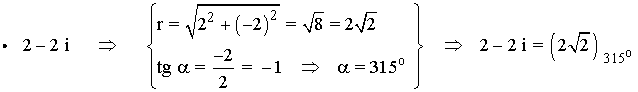
Sabemos que la tangente de un ángulo vale -1 en 45o y 315o .
Como el afijo es (2, -2) el ángulo está en el tercer cuadrante, es decir es 315o .
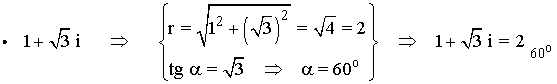
Como el afijo es (1, √3) el ángulo está en el primer cuadrante, es decir es 60o .
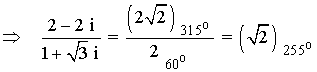
A continuación aplicamos la fórmula para encontrar las raíces cúbicas del número complejo:
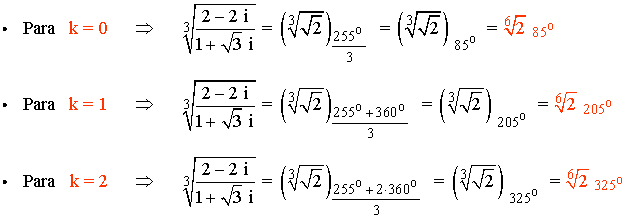
3) Halla las raíces sextas de la unidad
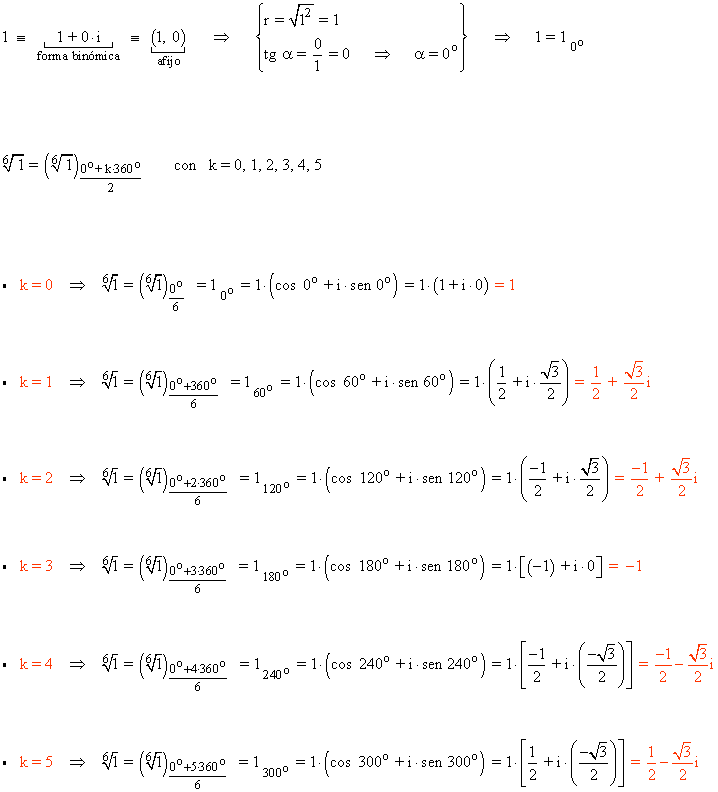
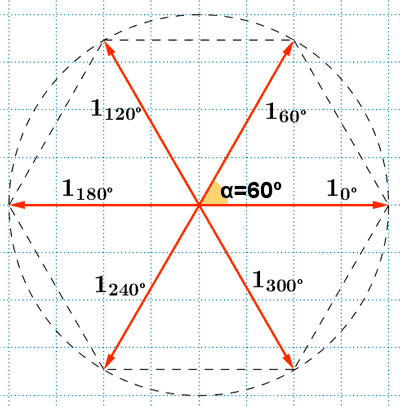
Por lo tanto, las raíces sextas de la unidad son:
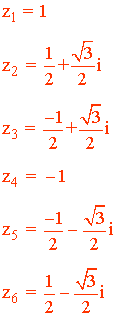


 INICIO
INICIO

