Ejercicios resueltos de números complejos en forma polar
1 ) Expresar en forma polar los siguientes complejos:
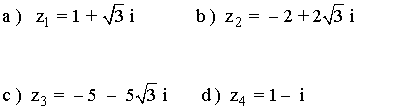
2 ) Expresar en forma polar los siguientes complejos.
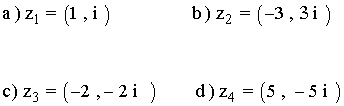
3 ) Escribir en la forma trigonométrica los siguientes números complejos.
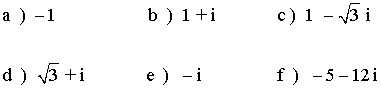
4 ) Expresar en forma binómica y con su afijo los siguientes complejos.
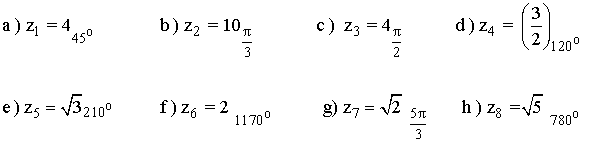
5 ) Expresar en forma polar y binómica, el conjugado y el opuesto de cada uno de los siguientes complejos.
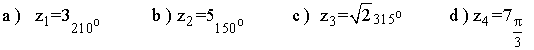
6 ) Calcula el inverso de los números complejos siguientes y represanta graficamente el resultado obtenido.
![]()
7 ) Hallar el módulo y el argumento de los siguientes complejos.

8 ) Realizar las siguientes operaciones:
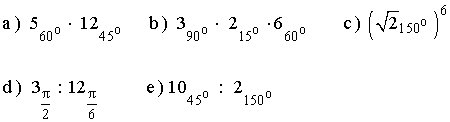
9 ) Realizar las siguientes operaciones y expresar la solución en forma binómica y con su afijo.
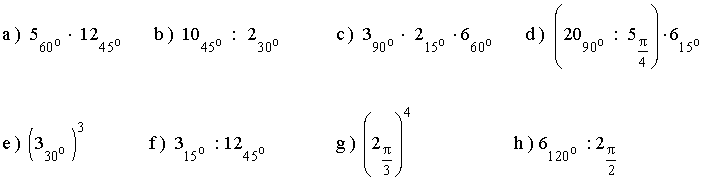
10 ) Calcula las potencias de los siguientes números complejos expresando el resultado en forma polar y binómica.
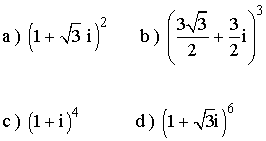
11 ) Calcula expresando el resultado en forma polar los siguientes potencias de complejos.
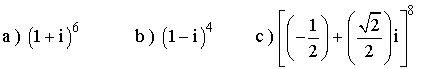
12 ) Expresa las siguientes potencias y expresa el resultado en forma polar.
![]()
13 ) Calcular las siguientes potencias en forma polar.
![]()
14 ) Dados los siguientes números complejos calcular:
![]()
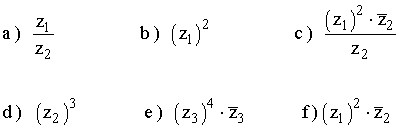
15 - a ) Calcula cos 75º y sen 75º mediante el producto de 130º y 145º
15 - b ) Halla las razones trigonométricas de 15º conociendo las de 45º y 30º mediante el cociente 145º y 130º
16 - a ) Calcula la cuarta potencia del número complejo 4 + 4v3 aplicando la fórmula de Moivre
16 - b ) Calcula aplicando la fórmula de Moivre: (1 + i)20
1 ) Expresar en forma polar los siguientes complejos:
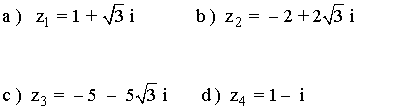
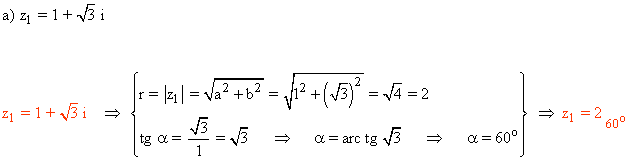
Sabemos que los ángulos que corresponden a la tangente de √3 son 60º y 240º.
Como el afijo de z es (1, √3) que está en el primer cuadrante, el ángulo del número complejo es 60o .
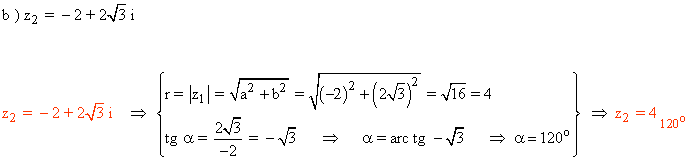
Sabemos que los ángulos que corresponden a la tangente de - √3 son 120º y 300º.
Como el afijo de z es (-2, 2 √3) que está en el segundo cuadrante, el ángulo del número complejo es 120o .
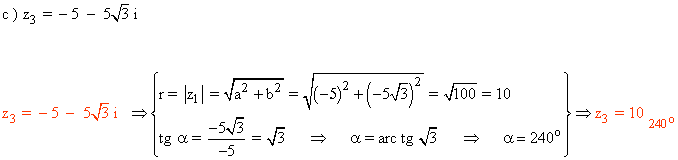
Sabemos que el ángulo que corresponden a la tangente de √3 es 60º y 240º. Como el afijo de z3 está en el tercer cuadrante, el ángulo del número complejo es 240o
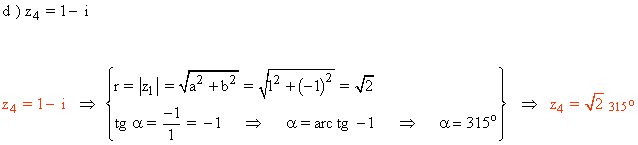
Sabemos que los ángulos que corresponden a la tangente de - 1 son 135º y 315º.
Como el afijo de z es (1, -1) que está en el cuarto cuadrante, el ángulo del número complejo es 315o .
Cuadro resumen:
| Forma binómica | Módulo | Cuadrante | Argumento | Forma polar |
|---|---|---|---|---|
| 2 | 1º | 60º | ||
| 4 | 2º | 120º | ||
| 10 | 3º | 240º | ||
| 4º | 315º |
2 ) Expresar en forma polar los siguientes complejos.
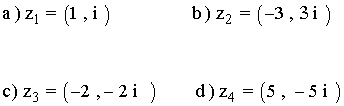
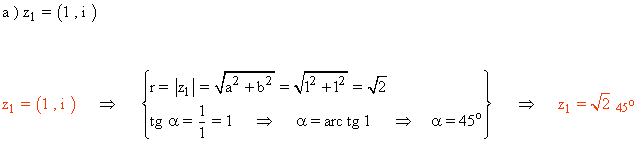
Sabemos que los ángulos que corresponden a la tangente de 1 son 45º y 225º.
Como el afijo de z es (1, 1) que está en el primer cuadrante, el ángulo del número complejo es 45o .
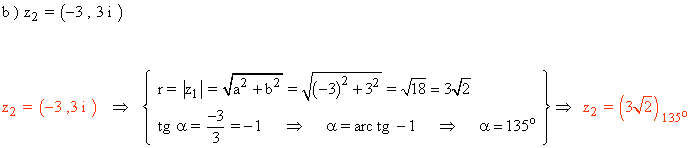
Sabemos que los ángulos que corresponden a la tangente de -1 son 135º y 315º.
Como el afijo de z es (-3, 3) que está en el segundo cuadrante, el ángulo del número complejo es 135o .
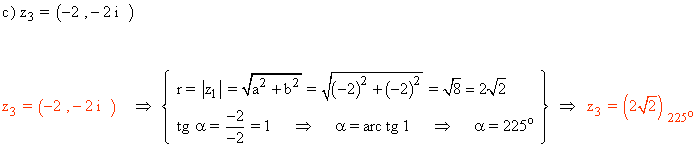
Sabemos que los ángulos que corresponden a la tangente de 1 son 45º y 225º.
Como el afijo de z es (-2, 2) que está en el tercer cuadrante, el ángulo del número complejo es 225o .
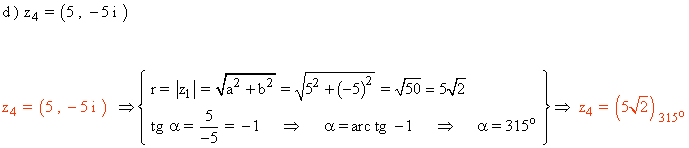
Sabemos que los ángulos que corresponden a la tangente de -1 son 135º y 315º.
Como el afijo de z es (5, -5) que está en el cuarto cuadrante, el ángulo del número complejo es 315o .
Cuadro resumen:
| Afijo | Módulo | Cuadrante | Argumento | Forma polar |
|---|---|---|---|---|
| 1º | 45º | |||
| 2º | 135º | |||
| 3º | 225º | |||
| 4º | 315º |
3 ) Escribir en la forma trigonométrica los siguientes números complejos.
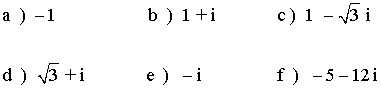
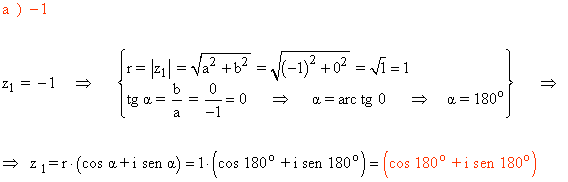
Sabemos que los ángulos que corresponden a la tangente de -√0 son 0º y 180º.
Como su afijo está en el eje negativo de la x, el ángulo del número complejo es 180o .
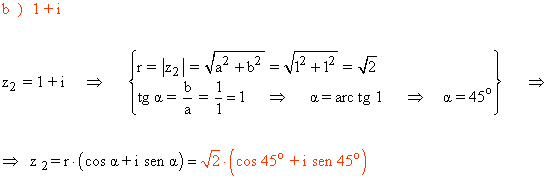
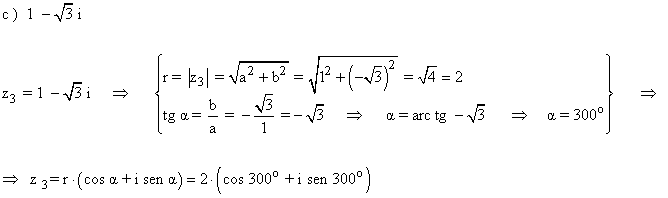
Sabemos que los ángulos que corresponden a la tangente de -√3 son 120º y 300º.
Como su afijo está en el cuarto cuadrante, el ángulo del número complejo es 300o .
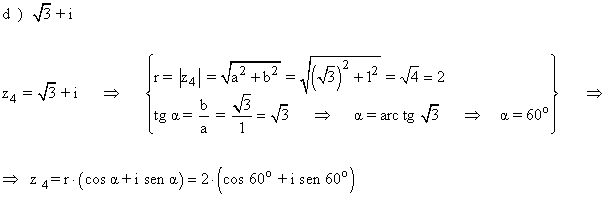
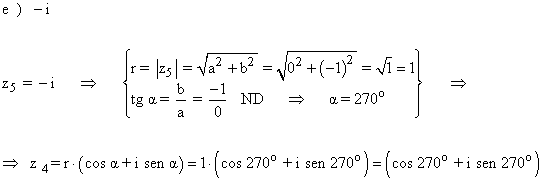
Sabemos que los ángulos que tenemos son 90o y 180o. Elegimos 180o puesto que estamos en el eje y negativo.
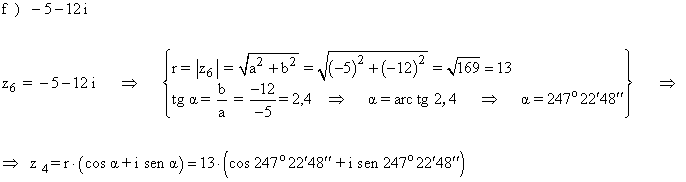
Sabemos que los ángulos que corresponden a la tangente de 12/5 son 67 º 22´ 48´´ y 247 º 22´ 48´´.
Como su afijo está en el cuarto cuadrante, el ángulo del número complejo es 247 º 22´ 48´´.
4 ) Expresar en forma binómica y con su afijo los siguientes complejos.
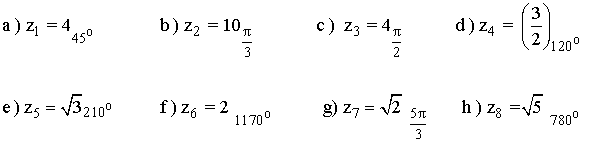
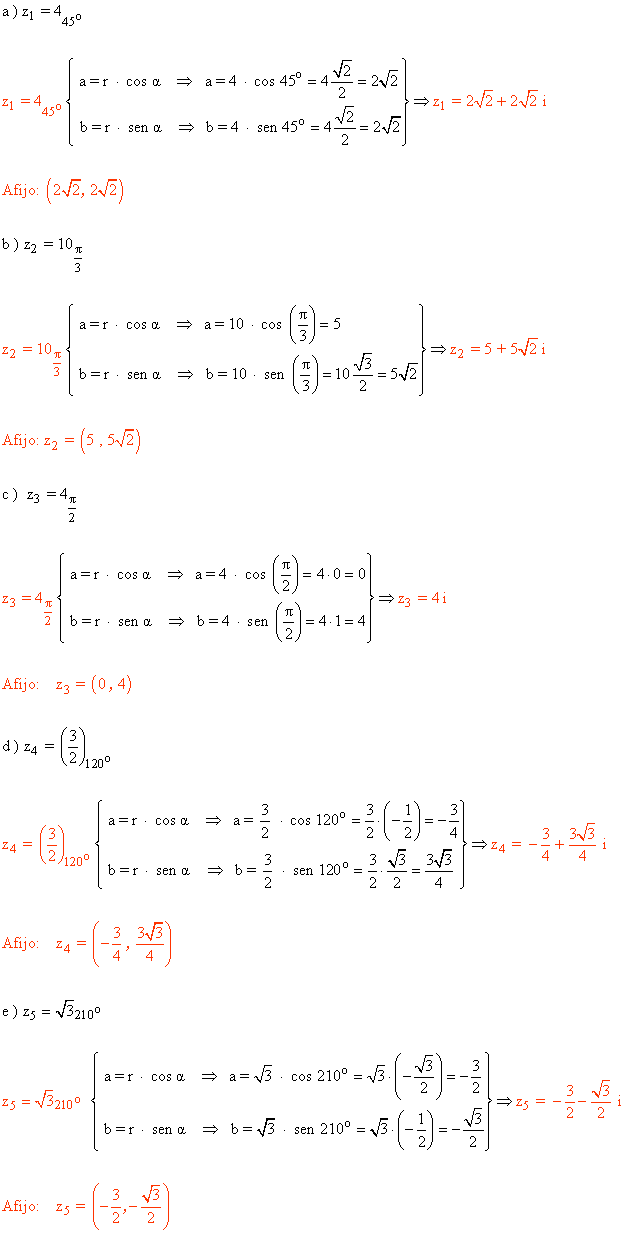
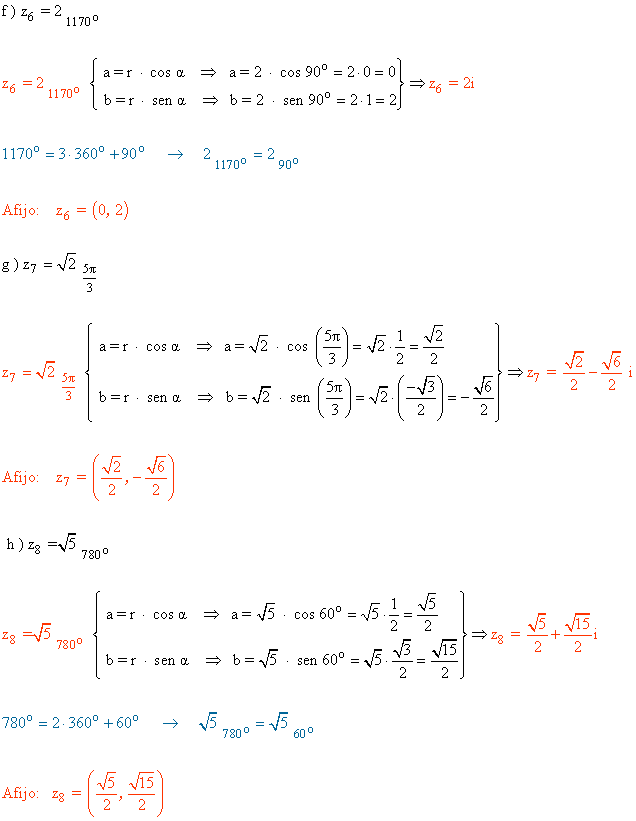
| Forma polar | a | b | Forma trigonómetrica | Forma binómica | Afijo |
|---|---|---|---|---|---|
 |
|||||
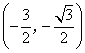 |
|||||
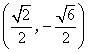 |
|||||
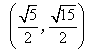 |
5 ) Expresar en forma polar y binómica, el conjugado y el opuesto de cada uno de los siguientes complejos.
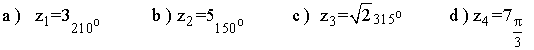
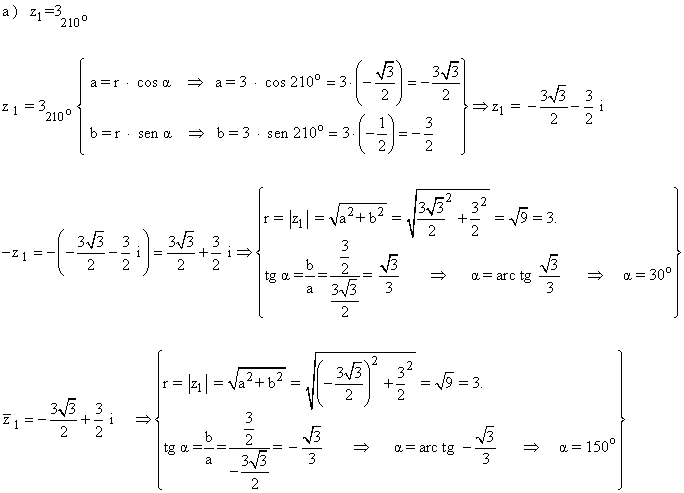
Sabemos que los ángulos que corresponden a la tangente de - (√3 /3) son 150º y 210º.
Como su afijo está en el segundo cuadrante, el ángulo del número complejo es 150o .
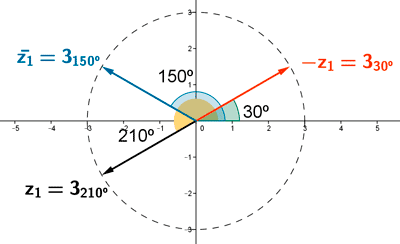
El conjugado de un número complejo es simétrico respecto del eje de abcisas.
El opuesto de un número complejo es simétrico respecto del origen.
Otro método:
El argumento de un numero complejo y el de su opuesto se diferencian en 180º.
El argumento de un numero complejo y el de su conjugado es el mismo pero de signo contrario puesto que se refleja en el eje OX.
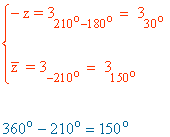
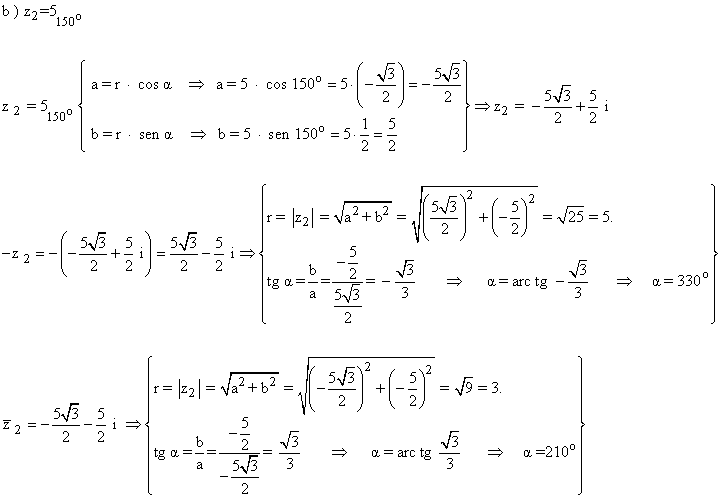
Sabemos que los ángulos que corresponden a la tangente de √3 /3 son 30º y 210º.
Como su afijo está en el tercer cuadrante, el ángulo del número complejo es 210o .
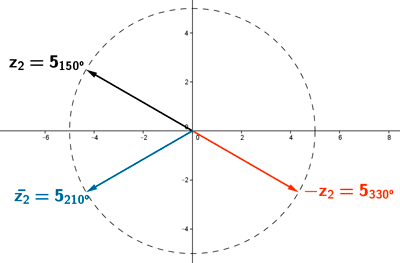
El conjugado de un número complejo es simétrico respecto del eje de abcisas.
El opuesto de un número complejo es simétrico respecto del origen.
Otro método:
El argumento de un numero complejo y el de su opuesto se diferencian en 180º.
El argumento de un numero complejo y el de su conjugado es el mismo pero de signo contrario puesto que se refleja en el eje OX.
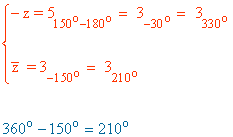
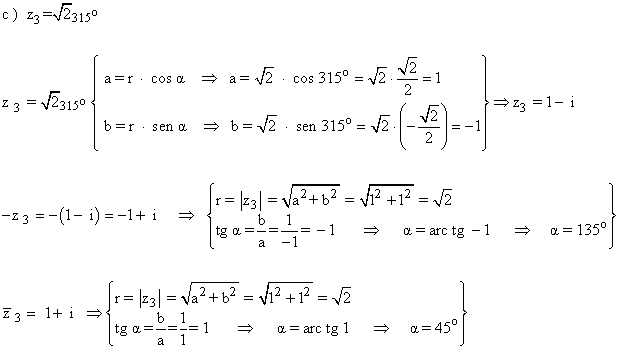
Sabemos que los ángulos que corresponden a la tangente de 1 son 45º y 225º.
Como su afijo está en el primer cuadrante, el ángulo del número complejo es 45o .
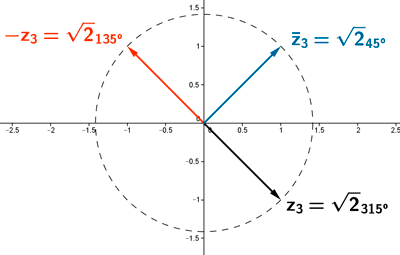
El conjugado de un número complejo es simétrico respecto del eje de abcisas.
El opuesto de un número complejo es simétrico respecto del origen.
Otro método:
El argumento de un numero complejo y el de su opuesto se diferencian en 180º.
El argumento de un numero complejo y el de su conjugado es el mismo pero de signo contrario puesto que se refleja en el eje OX.
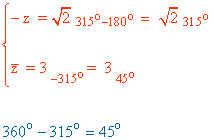

Sabemos que los ángulos que corresponden a la tangente de - √3 son 5π/3 y 2π/3.
Como su afijo está en el cuarto cuadrante, el ángulo del número complejo es 5π/3.
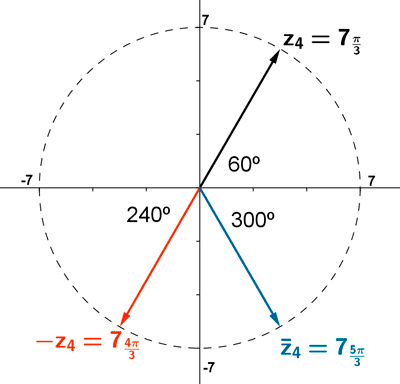
El conjugado de un número complejo es simétrico respecto del eje de abcisas.
El opuesto de un número complejo es simétrico respecto del origen.
Otro método:
El argumento de un numero complejo y el de su opuesto se diferencian en 180º.
El argumento de un numero complejo y el de su conjugado es el mismo pero de signo contrario puesto que se refleja en el eje OX.
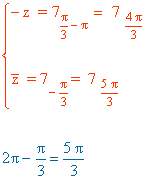
6 ) Calcula el inverso de los números complejos siguientes y represanta graficamente el resultado obtenido.
![]()
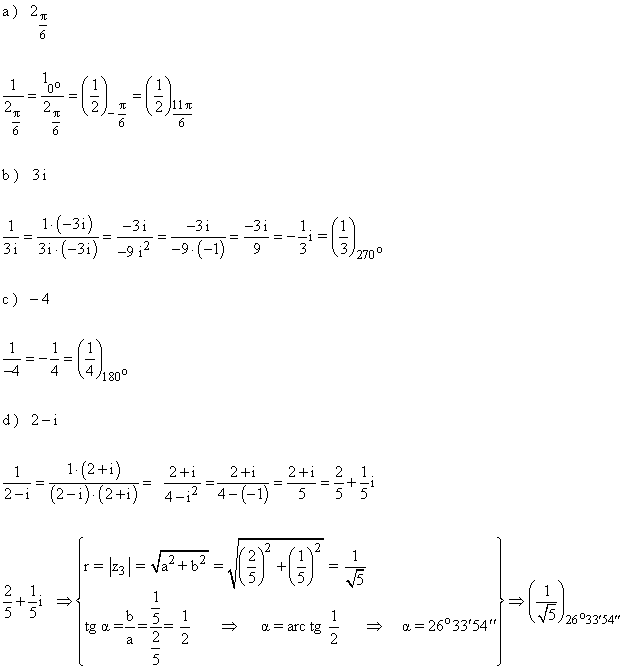
7 ) Hallar el módulo y el argumento de los siguientes complejos.

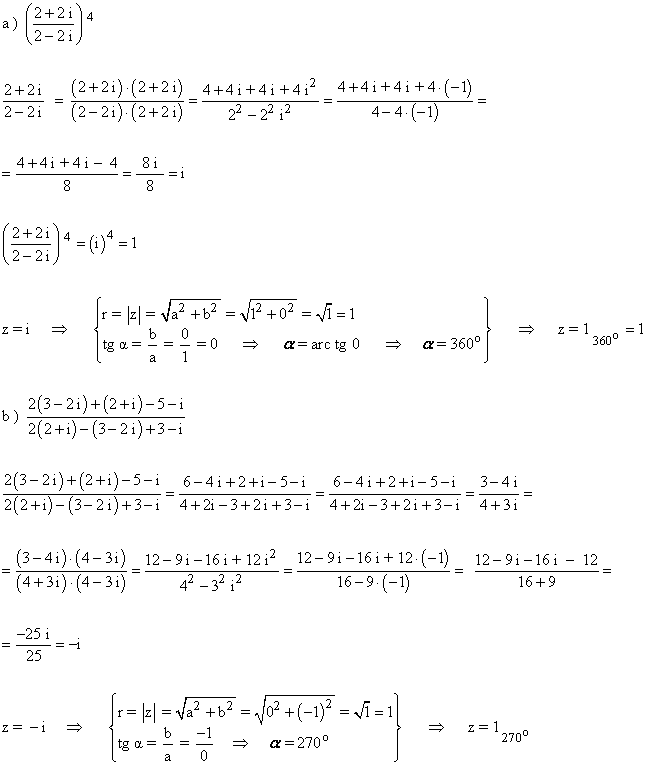
8 ) Realizar las siguientes operaciones:
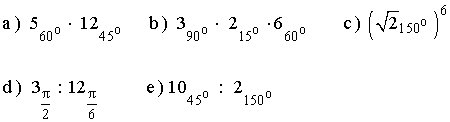
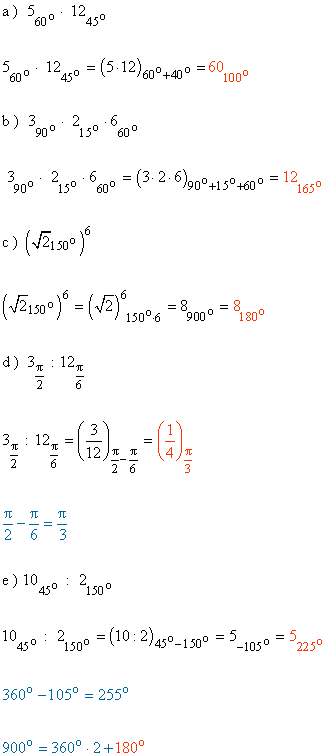
9 ) Realizar las siguientes operaciones:
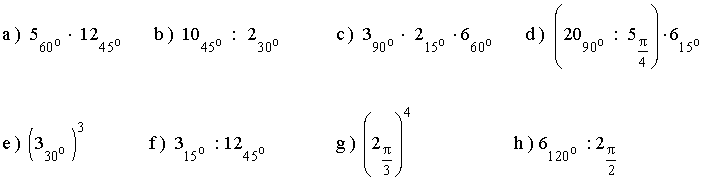
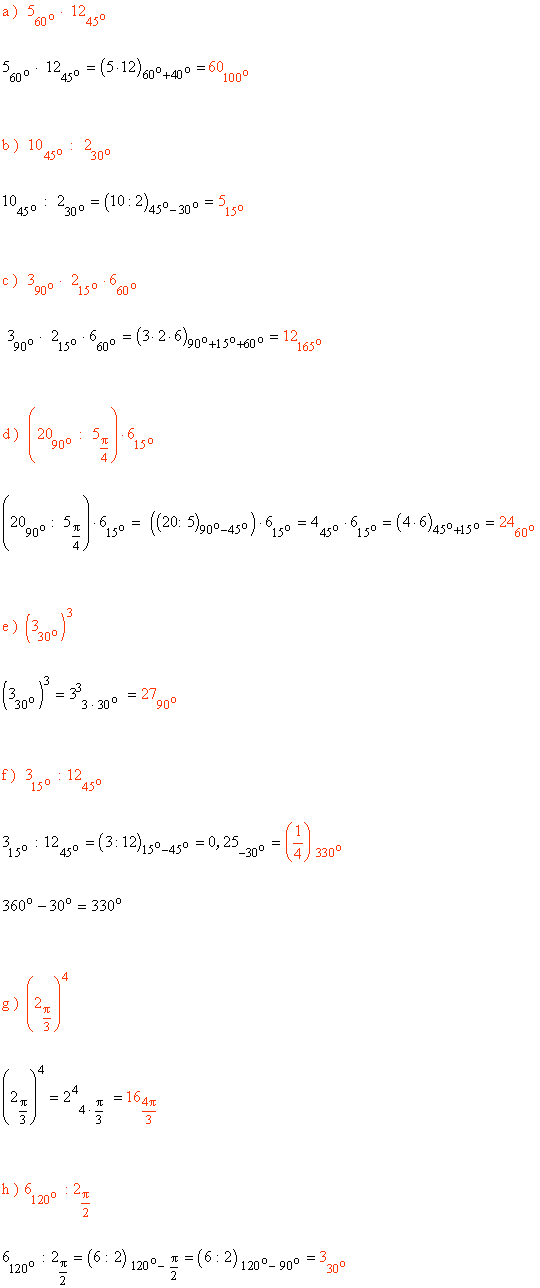
10 ) Calcula las potencias de los siguientes números complejos expresando el resultado en forma polar y binómica.
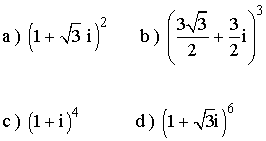
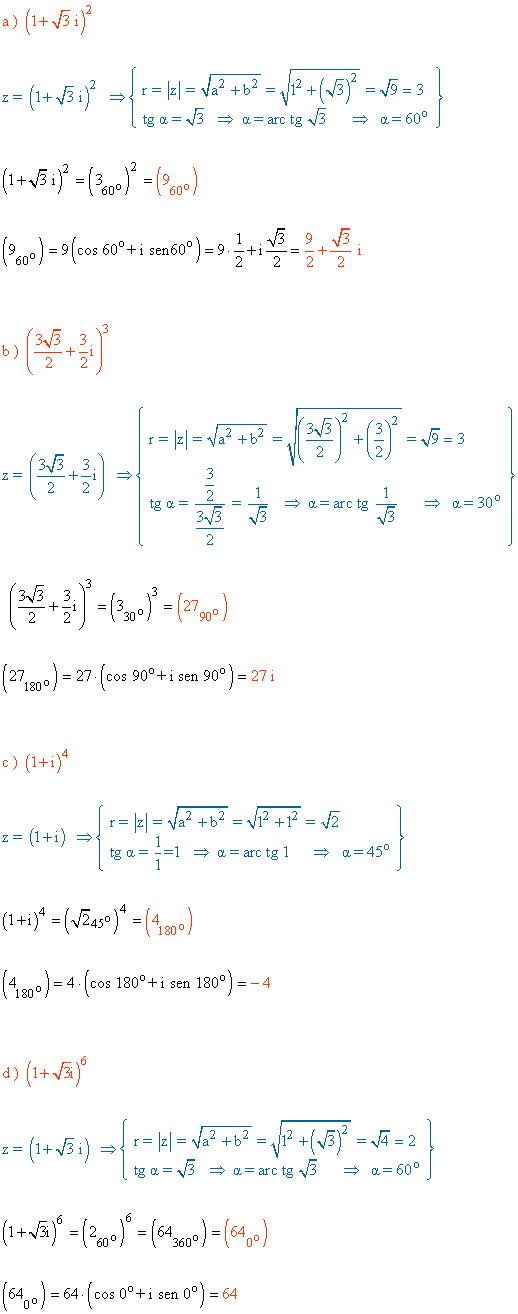
11 ) Calcula expresando el resultado en forma polar los siguientes potencias de complejos.
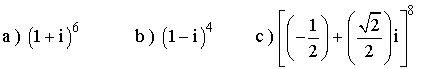
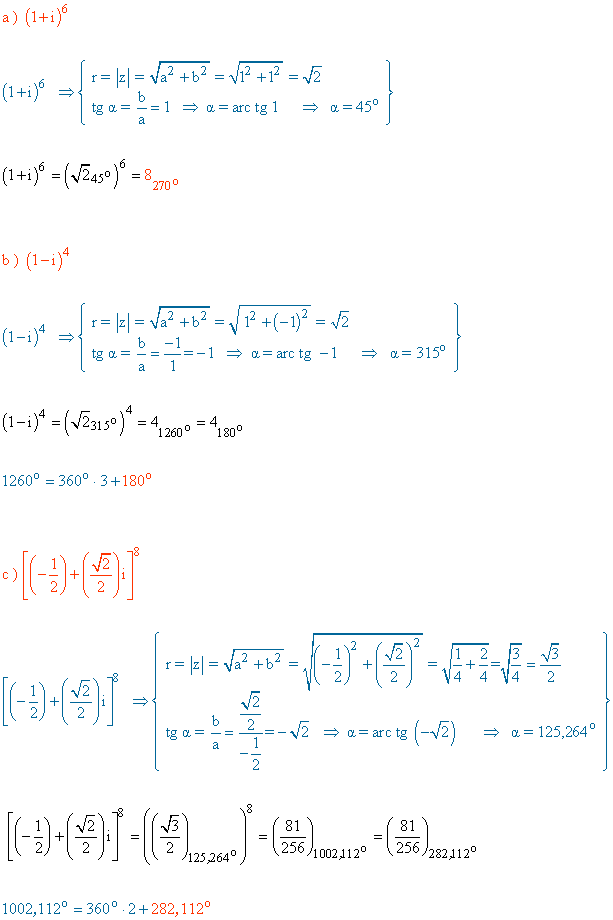
12 ) Expresa las siguientes potencias y expresa el resultado en forma polar.
![]()
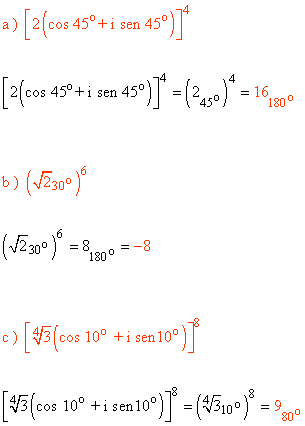
13 ) Calcular las siguientes potencias en forma polar.
![]()
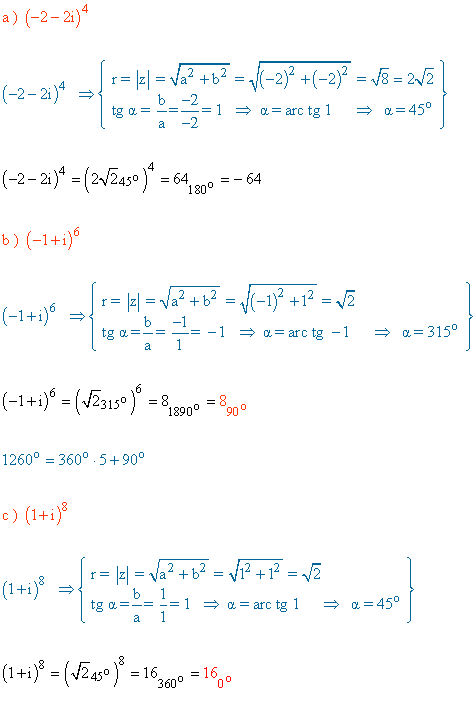
14 ) Dados los siguientes números complejos calcular:
![]()
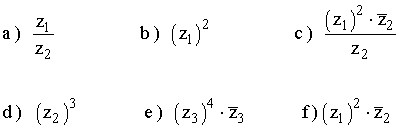
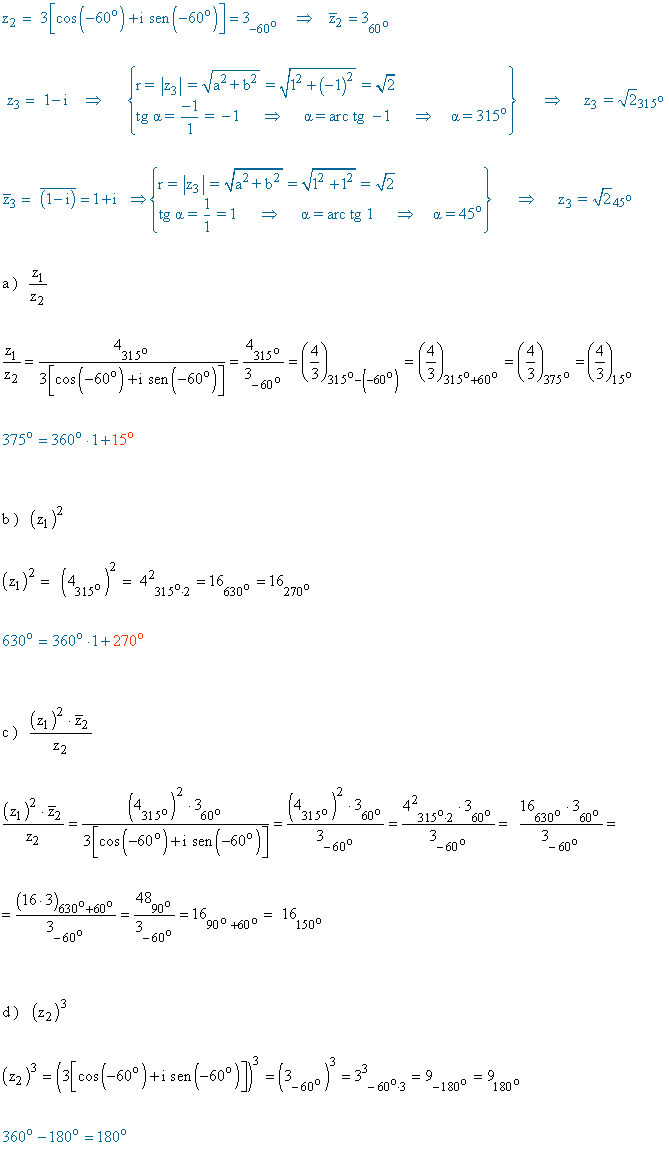
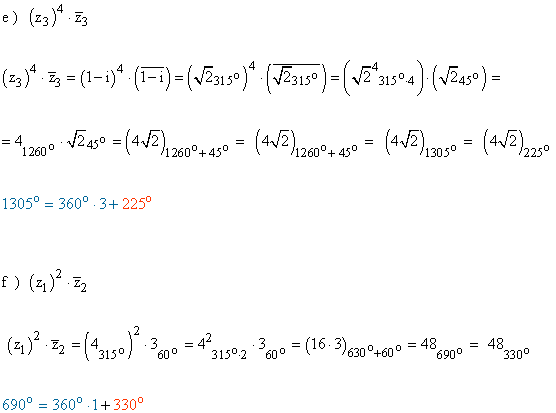
15 - a ) Calcula cos 75º y sen 75º mediante el producto de 130º y 145º
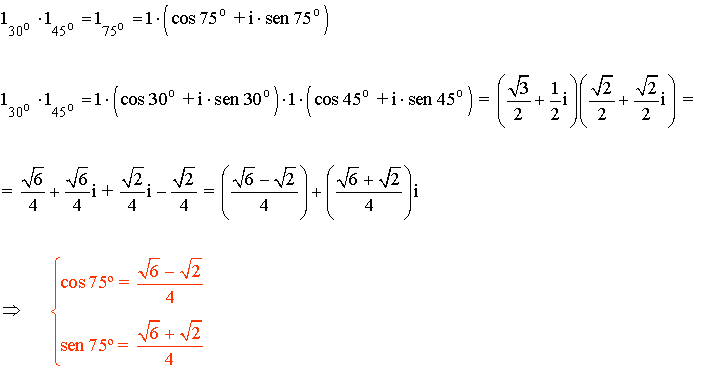
15 - b ) Halla las razones trigonométricas de 15º conociendo las de 45º y 30º mediante el cociente 145º y 130º
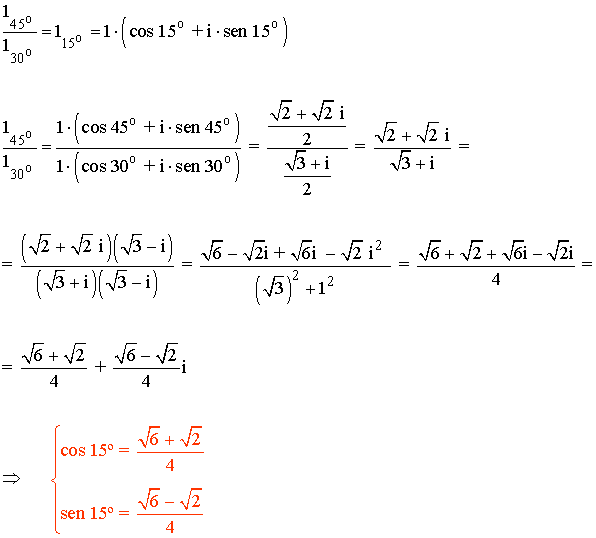
16 - a ) Calcula la cuarta potencia del número complejo 4 + 4v3 aplicando la fórmula de Moivre
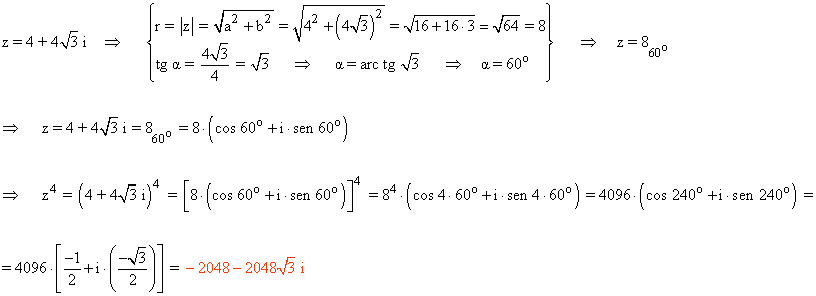
16 - b ) Calcula aplicando la fórmula de Moivre: (1 + i)20
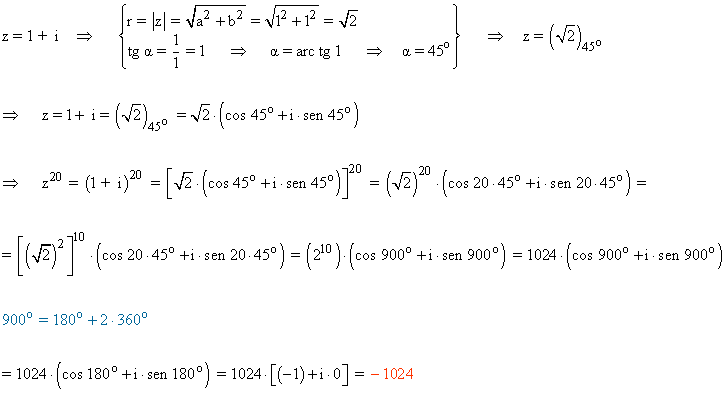


 INICIO
INICIO