Raíces complejas de una ecuación de segundo grado
y ecuaciones bicuadradas
Ecuaciones de segundo grado
En una ecuación de segundo grado con coeficientes reales ax2 + bx + c = 0 si el discriminante es negativo no tiene soluciones reales y las raíces son complejas conjugadas:
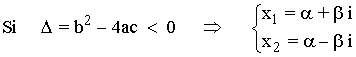
La interpretación geométrica es que la parábola no corta al eje OX siendo el eje de simetría y el vértice:

Ejemplo
Halla las raíces de la siguiente ecuación: x2 - 6x + 10 = 0
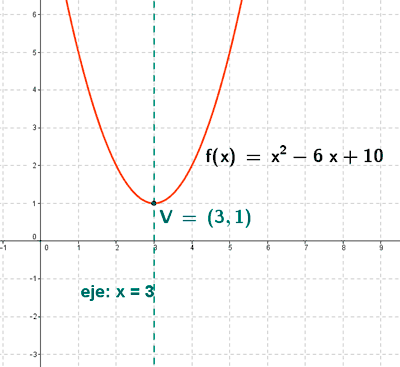
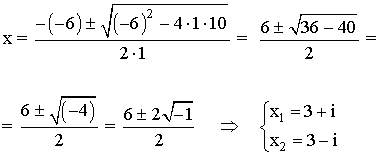
De esta forma, el eje de simetría y el vértice de la parábola son:

La parábola no corta al eje OX porque sus soluciones son imaginarias.
Conociendo las raíces hallar la ecuación
Si una ecuación de segundo grado tiene las raíces complejas conjugadas:
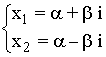
entonces la ecuación de segundo grado es:
![]()
Ejemplo:
Hallar la ecuación de segundo grado que tenga las raíces complejas conjugadas 3 ± i :
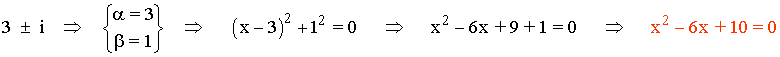
Método general:
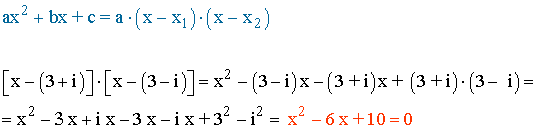
Otro método:

Ecuaciones bicuadradas
En el conjunto de los números complejos las ecuaciones bicuadradas tienen siempre 4 soluciones, que pueden ser:
• 4 soluciones reales
• 2 soluciones reales y 2 soluciones imaginarias conjugadas
• 2 pares de soluciones imaginarias conjugadas
Ejemplos:
1) Hallar las soluciones de la ecuación bicuadrada: x4 - 4x2 - 21 = 0
En primer lugar realizamos el cambio de variable t = x2 :
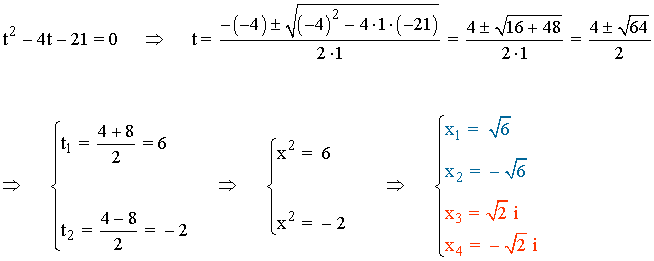
Por lo tanto la ecuación tiene dos números reales y dos números imaginarios conjugados.
2) Hallar las soluciones de la ecuación bicuadrada: x4 + 8x2 + 12 = 0
En primer lugar realizamos el cambio de variable t = x2 :
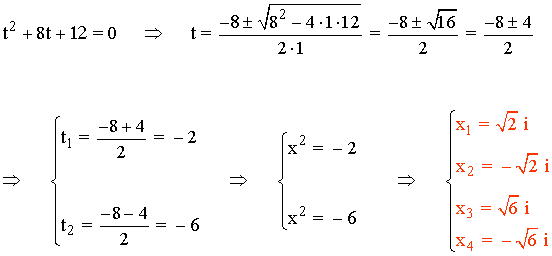
Por lo tanto la ecuación tiene dos pares de números imaginarios conjugados.


 INICIO
INICIO

