Ejercicios resueltos de ecuaciones y sistemas con números complejos
1 ) Dados los números complejos z1= 2 - i y z2= 3 + 6 i determinar el número x que verifica cada una de las siguientes igualdades.
![]()
2 ) Hallar las soluciones de las siguientes ecuaciones:

3 ) Hallar las soluciones de las siguientes ecuaciones y representalas:
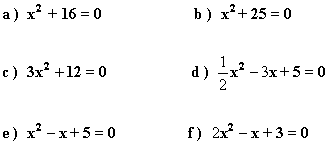
4 )
4-a ) Escribe una ecuación de segundo grado que tenga por soluciones 2 + i y 2 - i.
4-b ) Escribe una ecuación de segundo grado que tenga por soluciones 630º y 6-30º
4-c ) Comprueba que √2 i y 2 - i son soluciones de la ecuación x4-4x3+7x2-8x+10=0 y encuentra otras soluciones.
5 ) Hallar las soluciones de la siguiente ecuación:
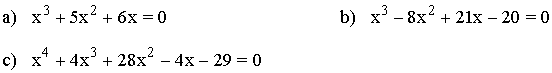
6 ) Hallar las soluciones de las siguientes ecuaciones:
![]()
7 ) Hallar las soluciones de las siguientes ecuaciones:
![]()
8 ) Hallar las soluciones de la siguiente ecuación y representar gráficamente:
z6 - 1 = 0
9 ) Hallar las soluciones de la siguiente ecuación y representar gráficamente:
z4 - 81 = 0
10 ) Resuelve las siguientes ecuaciones expresando la solución en forma polar, binómica y trigonométrica y representa gráficamente.

11 ) Resuelve las siguientes ecuaciones y representa gráficamente:
![]()
12 ) Resuelve las siguientes ecuaciones expresando el resultado en forma binómica:
![]()
13 ) Calcula las siguientes raíces expresando el resultado en forma polar y representándo gráficamente las soluciones.
![]()
14 ) Hallar las soluciones de la siguiente ecuación:
![]()
15 ) Hallar las soluciones de los siguientes sistemas de ecuaciones:

16 ) Hallar las soluciones del siguiente sistema de ecuaciones:

1 ) Dados los números complejos z1= 2 - i y z2= 3 + 6 i determinar el número x que verifica cada una de las siguientes igualdades.
![]()
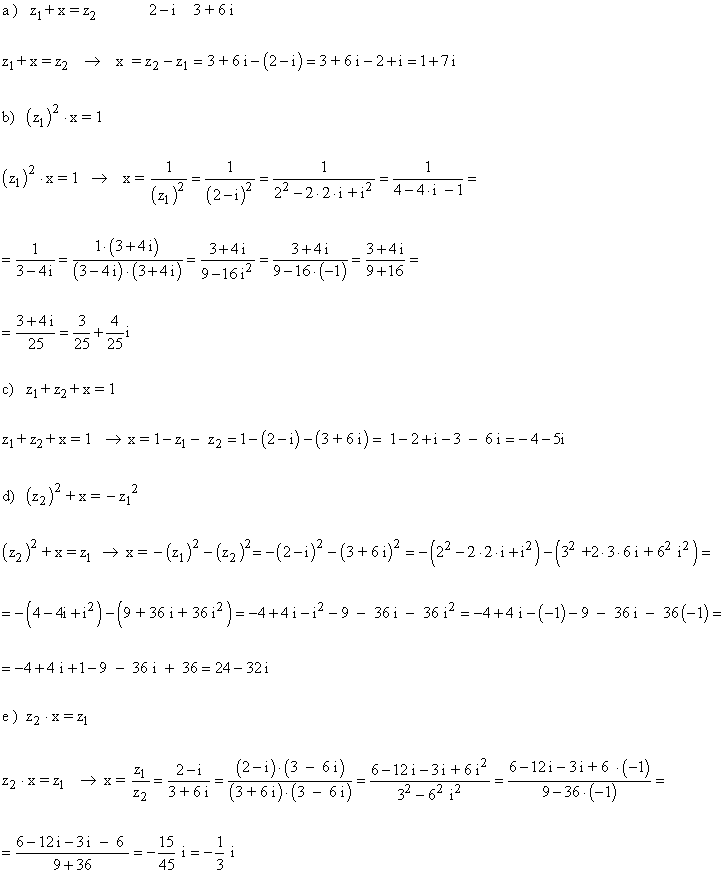
2 ) Hallar las soluciones de las siguientes ecuaciones:

![]()
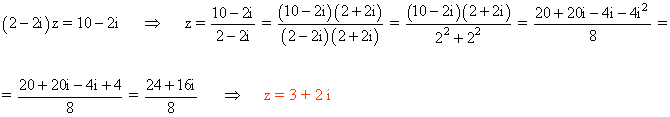
![]()
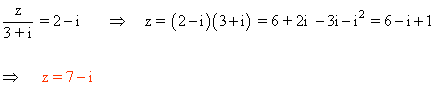
![]()

![]()
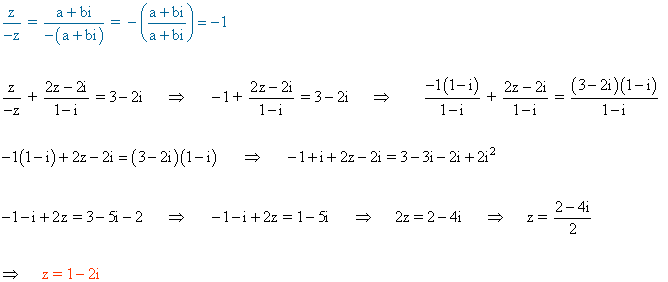
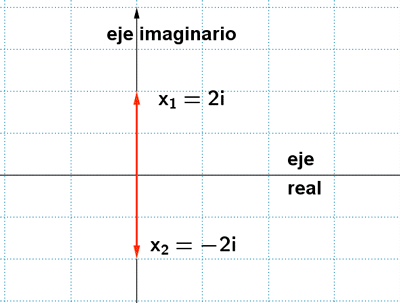
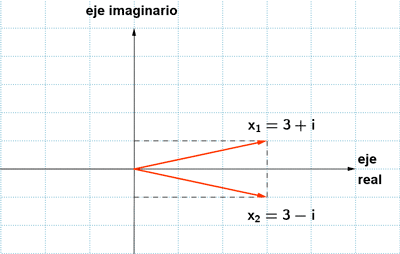
3 ) Hallar las soluciones de las siguientes ecuaciones y representalas:
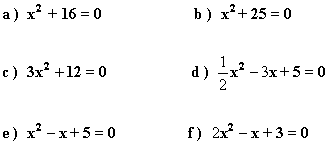
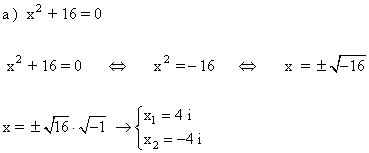
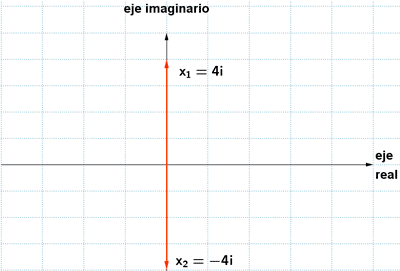
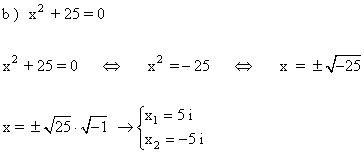
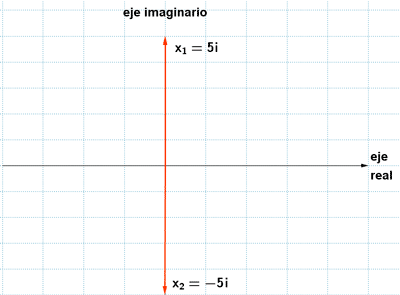
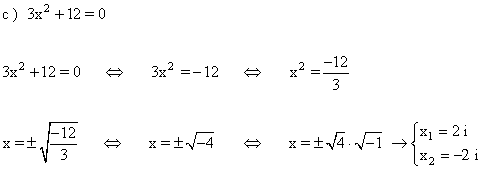
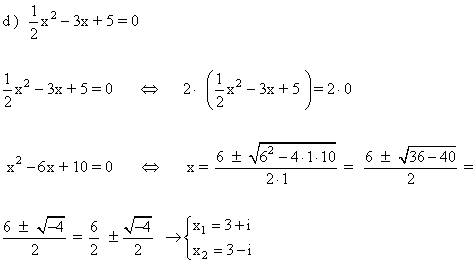
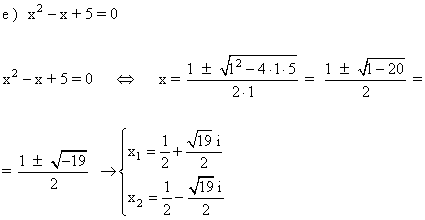
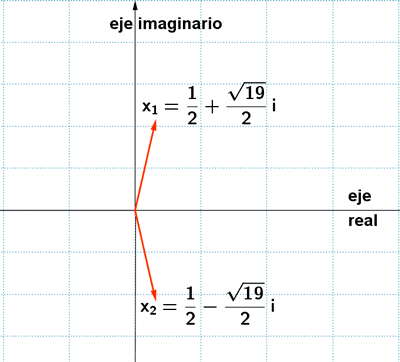
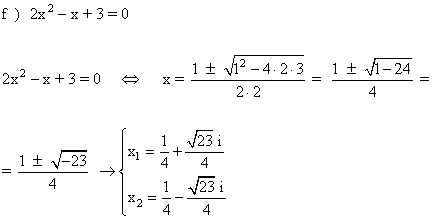
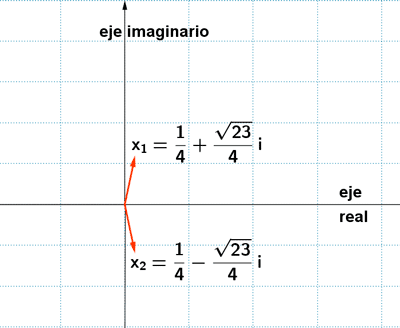
4-a ) Escribe una ecuación de segundo grado que tenga por soluciones 2 + i y 2 - i.

4-b ) Escribe una ecuación de segundo grado que tenga por soluciones 630º y 6-30º

4-c ) Comprueba que √2 i y 2 - i son soluciones de la ecuación x4-4x3+7x2-8x+10=0 y encuentra otras soluciones.
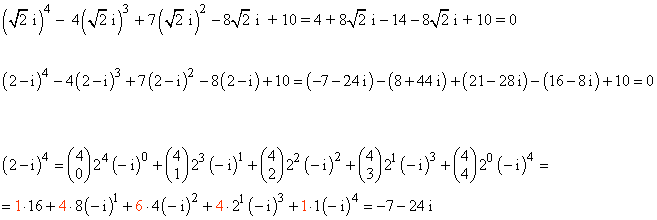
Las otras dos soluciones son los complejos conjugados:
![]()
5 ) Hallar las soluciones de la siguiente ecuación:
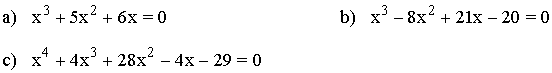
![]()
Factorizamos el polinomio, por lo que quedaría:
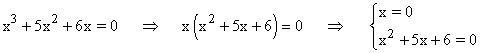
Para que el producto de dos factores sea 0 basta que uno de ellos sea 0, por lo tanto:
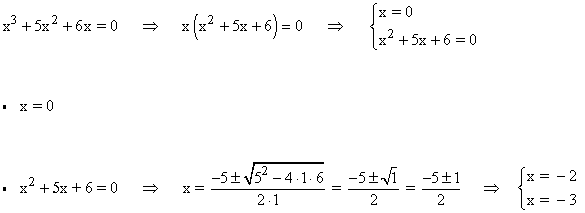
Por lo tanto la ecuación tiene tres soluciones tanto en los números reales como en los números complejos.
![]()
Aplicamos la regla de Ruffini con los divisores del término independiente:
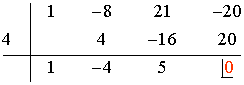
Por lo tanto la ecuación tiene una raíz real x = 4 y el polinomio se descompone de la siguiente forma:
![]()
Resolvemos la ecuación de segundo grado para calcular el resto de soluciones:
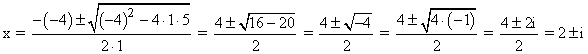
Por lo tanto la ecuación tiene una raíz real y dos raíces imaginarias conjugadas:
![]()
![]()
Aplicamos la regla de Ruffini con los divisores del término independiente. Además, como los coeficientes suman 0, sabemos por el teorema del resto que es divisible entre 1:
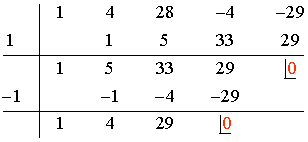
Por lo tanto la ecuación tiene dos raíces reales: x = 1 y x = -1 y se descompone de la siguiente manera::
![]()
Resolvemos la ecuación de segundo grado para calcular el resto de soluciones:
![]()
Por lo tanto la ecuación tiene dos raíces reales y dos raíces imaginarias conjugadas:
![]()
6 ) Hallar las soluciones de las siguientes ecuaciones:
![]()
![]()
En primer lugar realizamos el cambio de variable t = x2 :
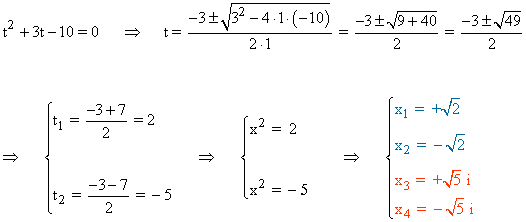
Por lo tanto la ecuación tiene dos números reales y dos números imaginarios conjugados.
![]()
En primer lugar realizamos el cambio de variable t = x2 :
t2 + 2t + 1 = 0 ⇒ Trinomio cuadrado perfecto: (t + 1)2 = 0 ⇒ t = -1 (raíz doble)
![]()
Por lo tanto la ecuación no tiene soluciones en R, y las soluciones en C son x = i y x = - i ambas dobles.
![]()
En primer lugar realizamos el cambio de variable t = x3 :
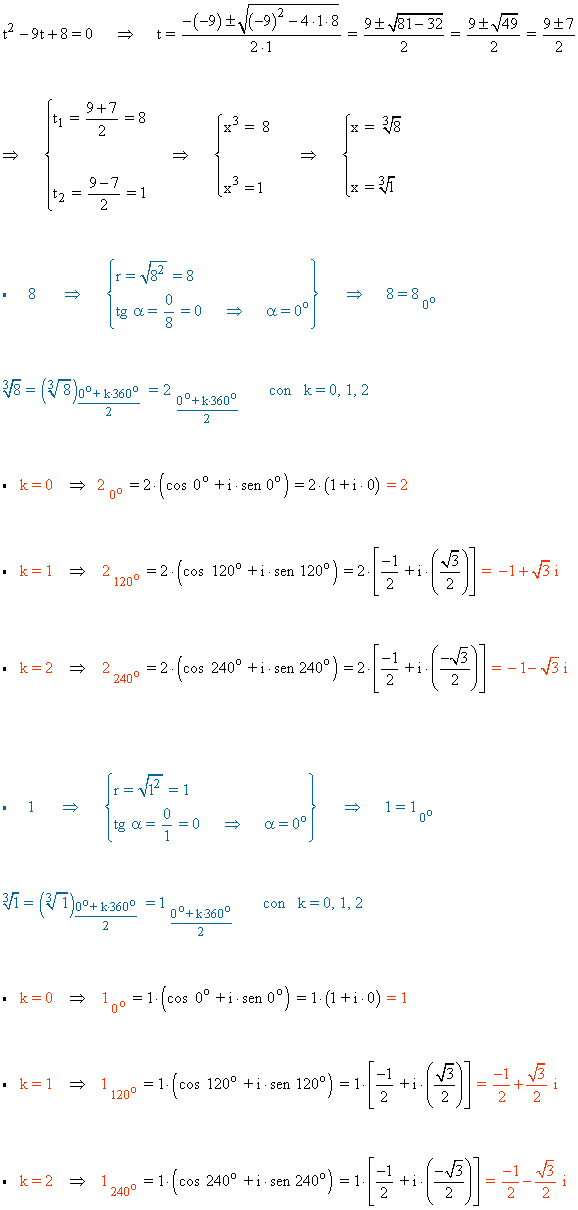
Por tanto las seis raíces de la ecuación son:
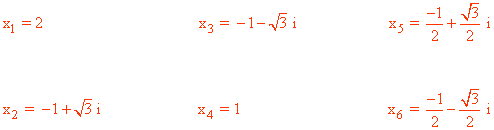
7 ) Hallar las soluciones de las siguientes ecuaciones:
![]()
![]()
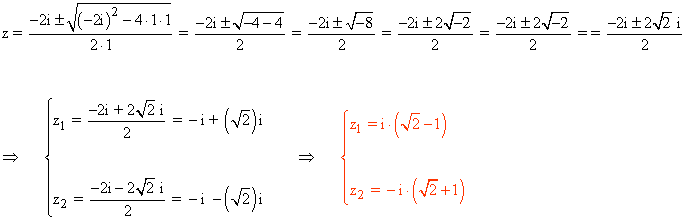
Por lo tanto la ecuación tiene dos soluciones imaginarias.
![]()
En primer lugar realizamos el cambio de variable t = x2 :
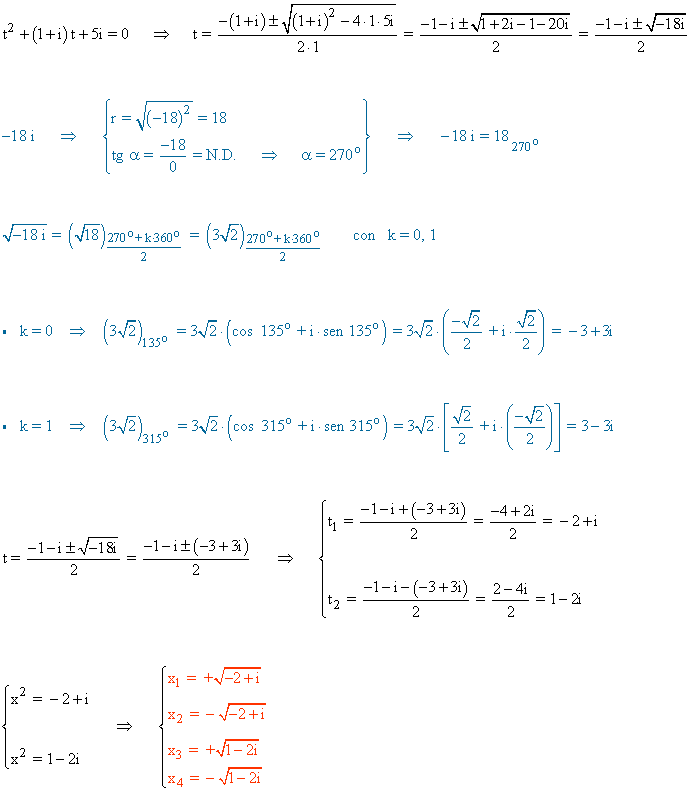
8 ) Hallar las soluciones de la siguiente ecuación y representar gráficamente:
z6 - 1 = 0
Resolviendo la ecuación en el conjunto de los números reales obtenemos dos soluciones:
![]()
Para obtener las seis raíces o soluciones en el conjunto de los números complejos:
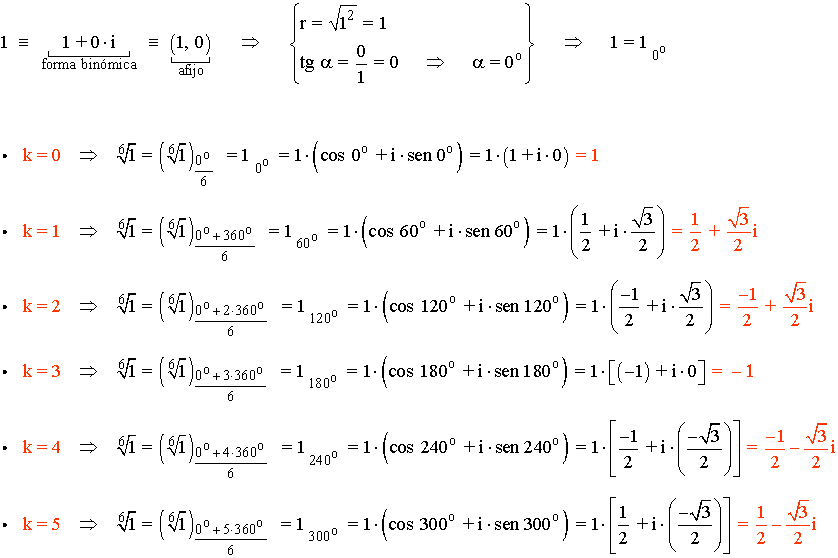
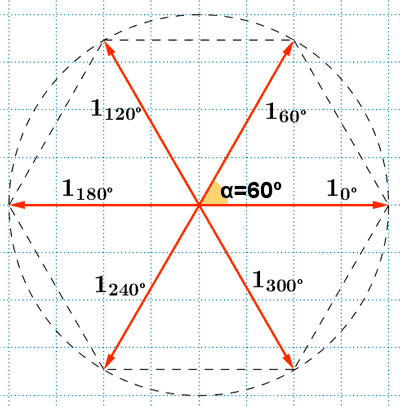
Por lo tanto, las raíces sextas de la unidad son:
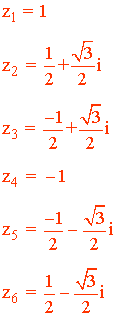
9 ) Hallar las soluciones de la siguiente ecuación y representar gráficamente:
z4 - 81 = 0
Resolviendo la ecuación en el conjunto de los números reales obtenemos dos soluciones:
![]()
Para obtener las cuatro raíces o soluciones en el conjunto de los números complejos:
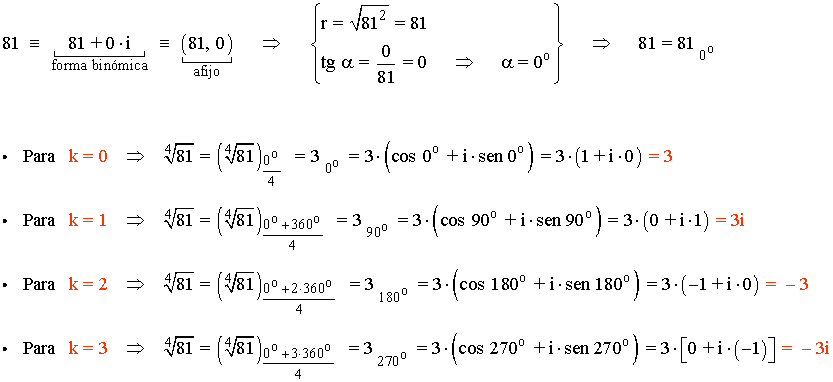
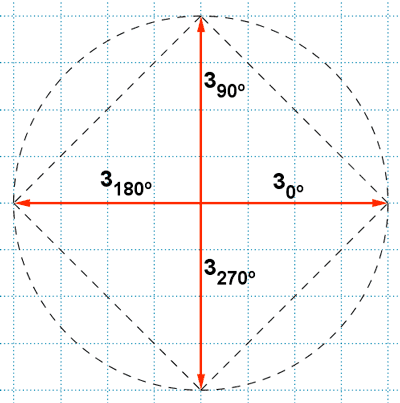
Por lo tanto, las cuatro raíces de la ecuación son:
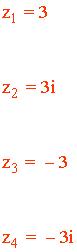
10 ) Resuelve las siguientes ecuaciones expresando la solución en forma polar, binómica y trigonométrica y representa gráficamente.

![]()
![]()
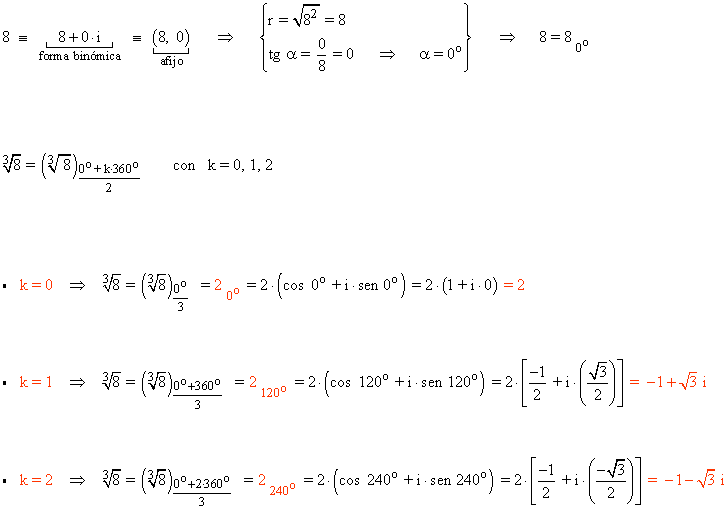
![]()
![]()
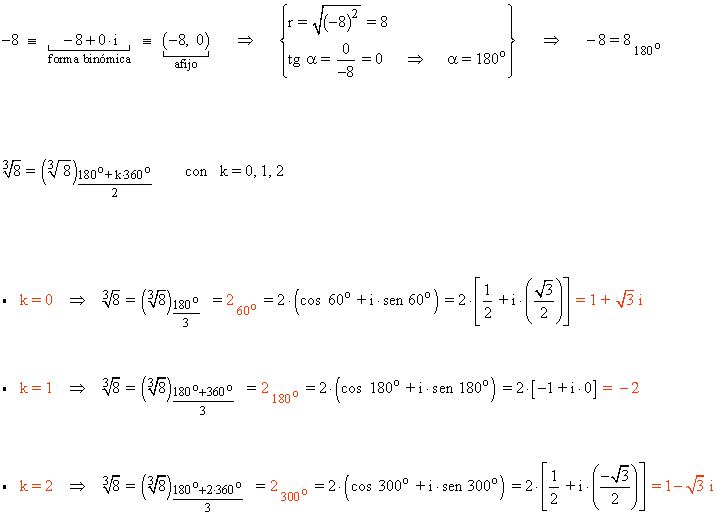
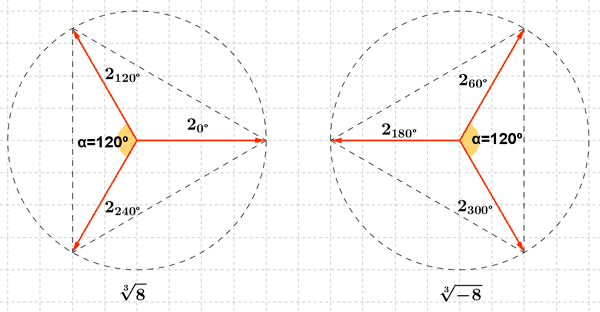
![]()
![]()
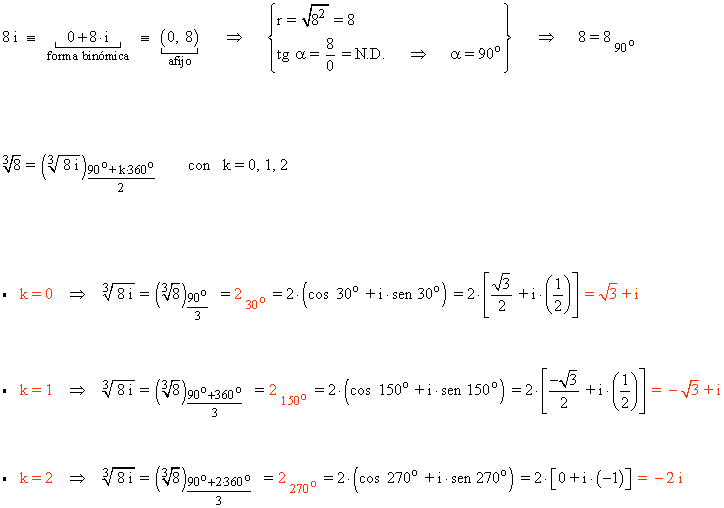
![]()
![]()
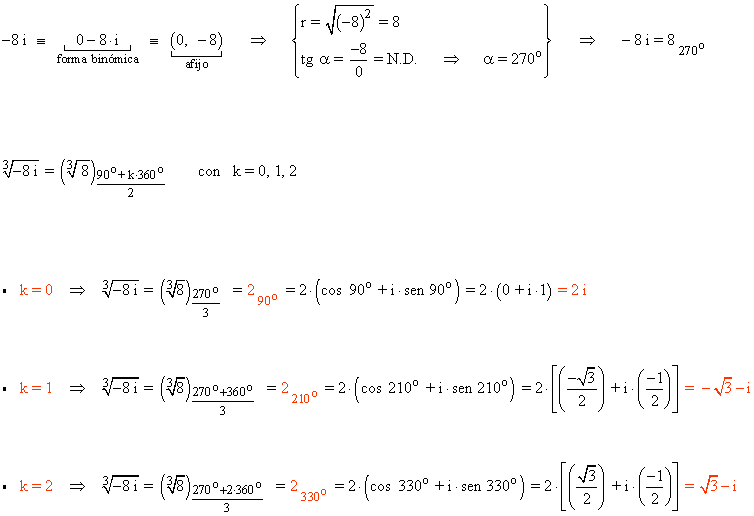
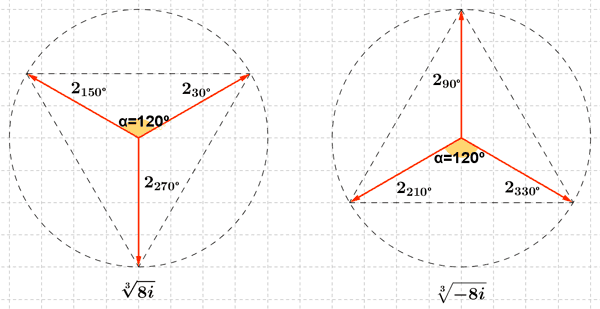
11 ) Resuelve las siguientes ecuaciones y representa gráficamente:
![]()
![]()
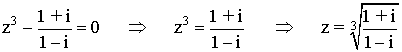
En primer lugar pasamos el número complejo a forma polar:
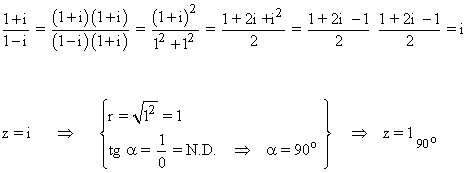
Sabemos que la tangente no está definida en 90o y 270o . Como el afijo de z es (0, 1) el ángulo del número complejo es 90o . A continuación aplicamos la fórmula para encontrar las raíces cúbicas de z:
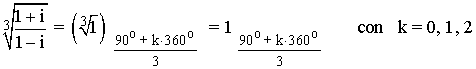
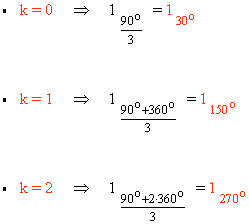
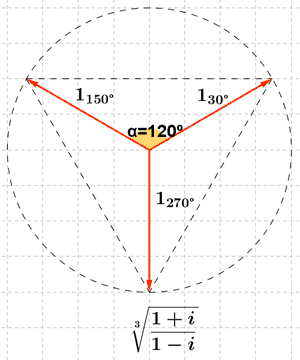
![]()
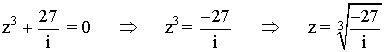
En primer lugar pasamos el número complejo a forma polar:
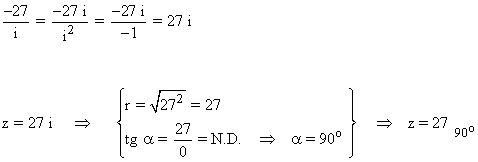
Sabemos que la tangente no está definida en 90o y 270o . Como el afijo de z es (0, 27) el ángulo del número complejo es 90o . A continuación aplicamos la fórmula para encontrar las raíces cúbicas de z:
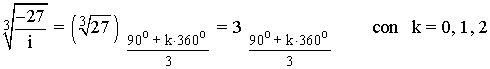
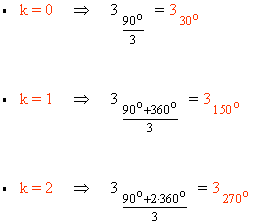
12 ) Resuelve las siguientes ecuaciones expresando el resultado en forma binómica:
![]()
![]()
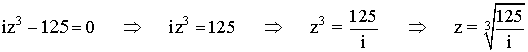
En primer lugar pasamos el número complejo a forma polar:
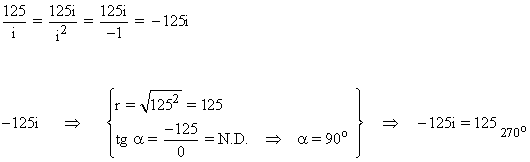
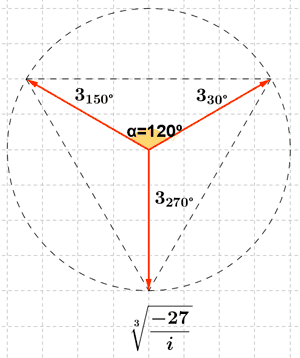
Sabemos que la tangente no está definida en 90o y 270o . Como el afijo de z es (0, -125) el ángulo del número complejo es 270o . A continuación aplicamos la fórmula para encontrar las raíces cúbicas:
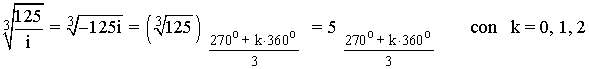
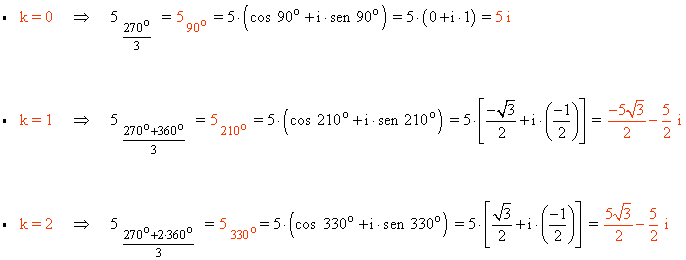
![]()
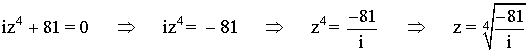
En primer lugar pasamos el número complejo a forma polar:
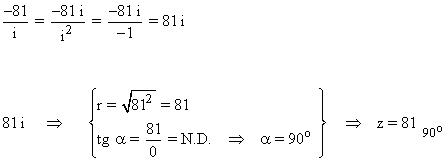
Sabemos que la tangente no está definida en 90o y 270o . Como el afijo de z es (0, 81) el ángulo del número complejo es 90o . A continuación aplicamos la fórmula para encontrar las raíces cuartas:
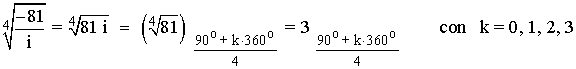
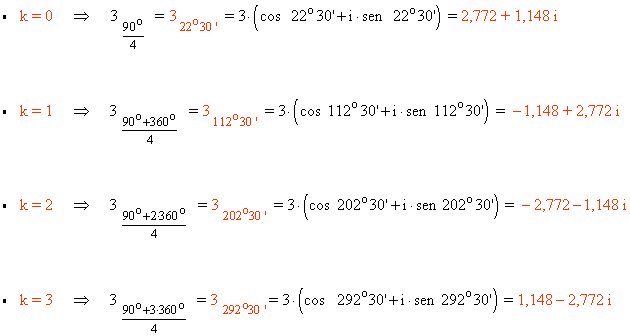
13 ) Calcula las siguientes raíces expresando el resultado en forma polar y representándo gráficamente las soluciones.
![]()
![]()
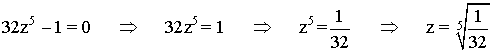
En primer lugar pasamos el número complejo a forma polar:

Sabemos que la tangente de un ángulo es 0 en 0o y 180o . Como el afijo de z es (1/32, 0) el ángulo del número complejo es 0o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
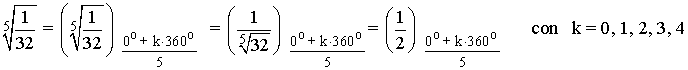
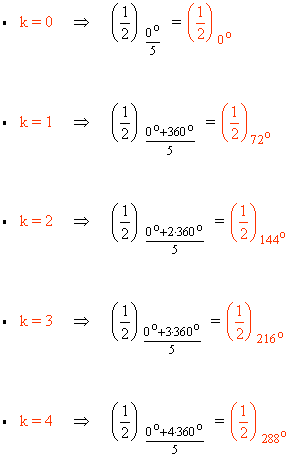
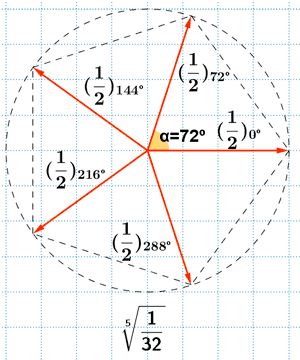
![]()
![]()
En primer lugar pasamos el número complejo a forma polar:
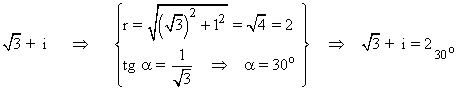
Como el afijo es (√3, 1) , es decir, está en el primer cuadrante, entonces el ángulo del número complejo es 30o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
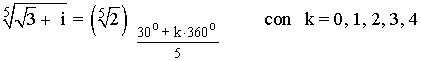
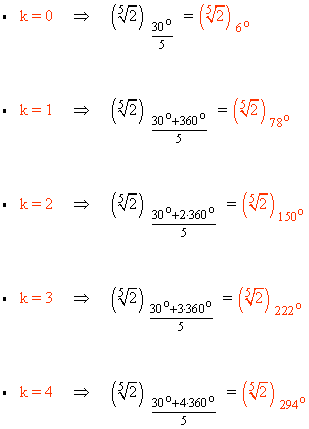
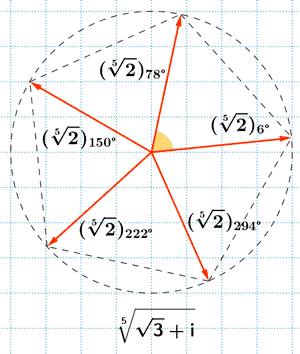
14 ) Hallar las soluciones de la siguiente ecuación:
![]()
Buscamos un número complejo z = x + y i que verifique la ecuación anterior:
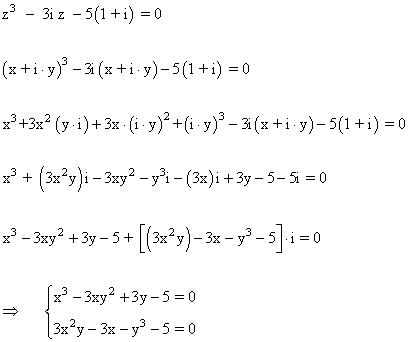
Para resolver el sistema, restamos ambas ecuaciones, resultando lo siguiente:
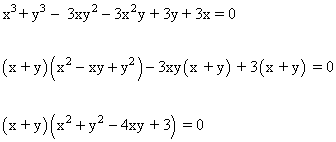
Por lo tanto una condición es que: x + y = 0 ⇒ y = - x
Sustituimos el valor de y en la primera ecuación del sistema:
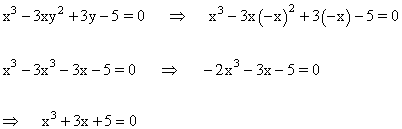
Aplicamos la regla de Ruffini con los divisores del término independiente: -1 , 1 , -5 y +5
La ecuación de tercer grado es divisible por x = -1 siendo la única solución real.
Ahora sustituimos el valor de x en la segunda ecuación del sistema:
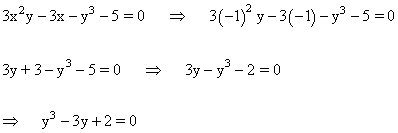
Aplicando de nuevo la regla de Ruffini se obtienen las siguientes soluciones: y = 1 (doble) y = 2
Las únicas soluciones de la parte real y la parte imaginaria que cumplen la condición x + y = 0 son:
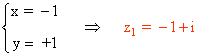
Dividiendo la ecuación primitiva entre la solución obtenida:
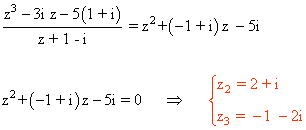
15 ) Hallar las soluciones de los siguientes sistemas de ecuaciones:

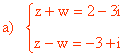
Utilizamos el método de reducción, es decir, sumamos ambas ecuaciones:
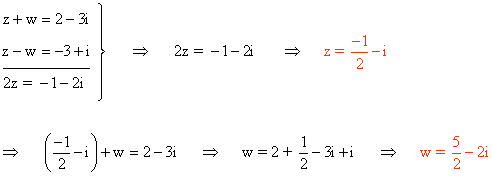
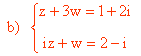
Utilizamos el método de reducción, multiplicando la segunda ecuación por 3 y se la restamos a la primera:
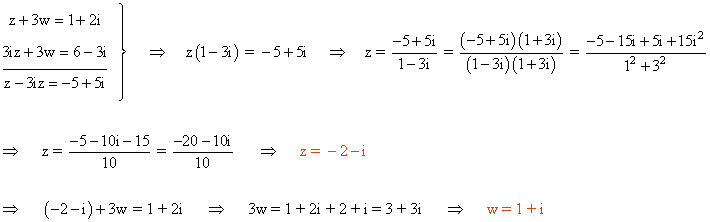
16 ) Hallar las soluciones del siguiente sistema de ecuaciones:

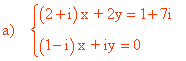
Utilizamos el método de sustitución despejando la variable y en la segunda ecuación:
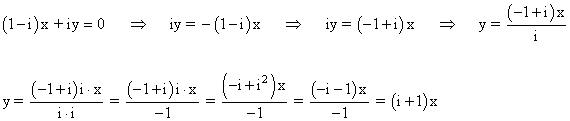
Sustituimos el valor de y en la primera ecuación:
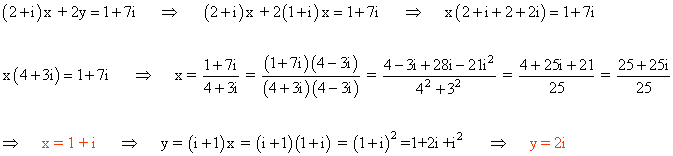
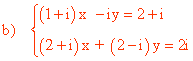
Si restamos ambas ecuaciones obtenemos la siguiente expresión:
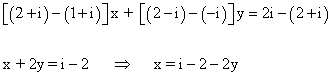
Utilizamos el método de sustitución en la primera ecuación:
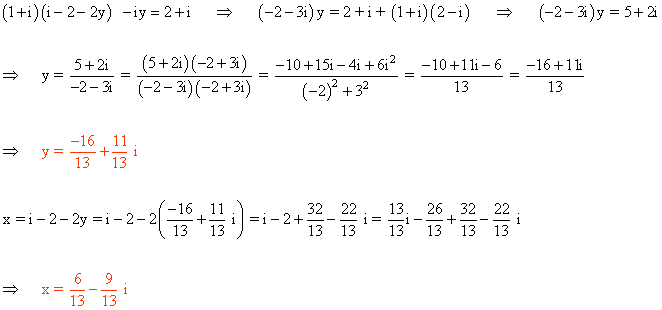


 INICIO
INICIO