Ejercicios resueltos de raíces de números complejos en forma polar
1) Hallar la raíz cuadrada de los siguientes números complejos:
a) 5 + 12 i b) 1 / (3 + 4 i)
2) Halla las siguientes raíces expresando el resultado en forma polar.

3) Calcula y expresa en forma polar:
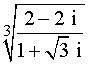
4) Calcula y expresa en forma polar:

5) Halla las raíces sextas de la unidad expresando el resultado en forma polar, binómica y trigonométrica y representa gráficamente.
![]()
6) Halla las raíces cuartas de 81 expresando el resultado en forma polar, binómica y trigonométrica y representa gráficamente.
![]()
7) Calcula las siguientes raíces expresando el resultado en forma polar, binómica y trigonométrica y representa gráficamente.

8) Calcula las siguientes raíces expresando el resultado en forma polar.

9) Calcula las siguientes raíces expresando el resultado en forma polar.
![]()
10) Calcula las siguientes raíces expresando el resultado en forma polar.

11) Calcula las siguientes raíces expresando el resultado en forma polar.
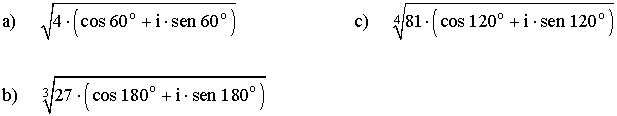
1) Hallar la raíz cuadrada de los siguientes números complejos:
a) 5 + 12 i b) 1 / (3 + 4 i)
a) 5 + 12 i
En primer lugar pasamos el número complejo a forma polar:
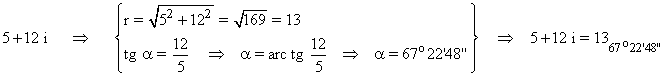
Como el afijo es (5, 12) el ángulo del número complejo está en el primer cuadrante..
A continuación aplicamos la fórmula para encontrar las raíces cuadradas:
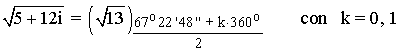
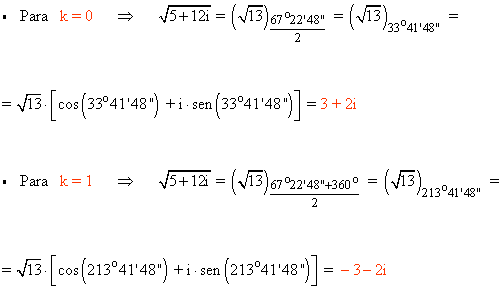
b) 1 / (3 + 4 i)
En primer lugar pasamos el número complejo a forma polar:
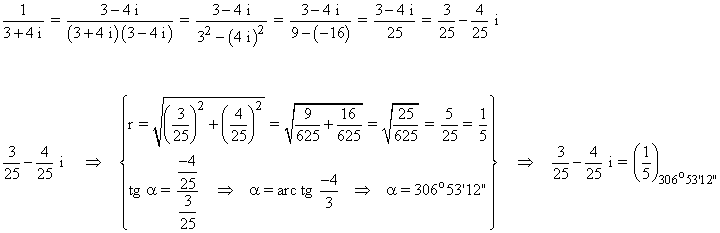
Como el afijo es (3/25, -4/25) el ángulo del número complejo está en el cuarto cuadrante..
A continuación aplicamos la fórmula para encontrar las raíces cuadradas:
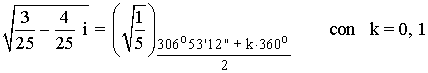
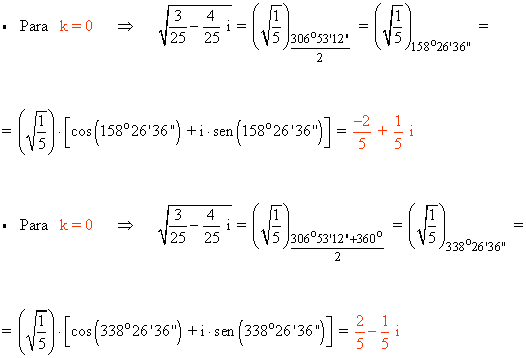
2) Calcula las siguientes raíces expresando el resultado en forma polar.

![]()
En primer lugar pasamos el número complejo a forma polar:
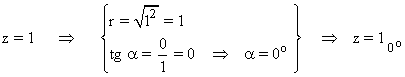
Sabemos que la tangente de un ángulo vale 0 en 0o y 180o . Como el afijo de z es (1, 0) el ángulo del número complejo es 0o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
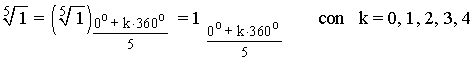
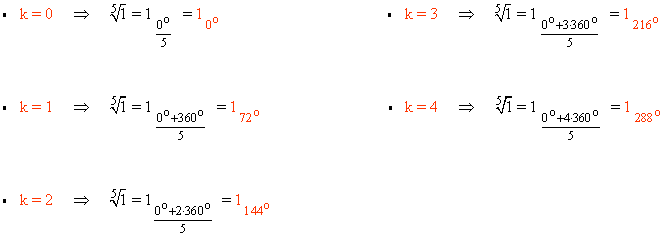
![]()
En primer lugar pasamos el número complejo a forma polar:
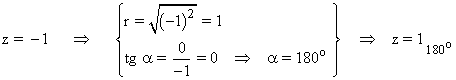
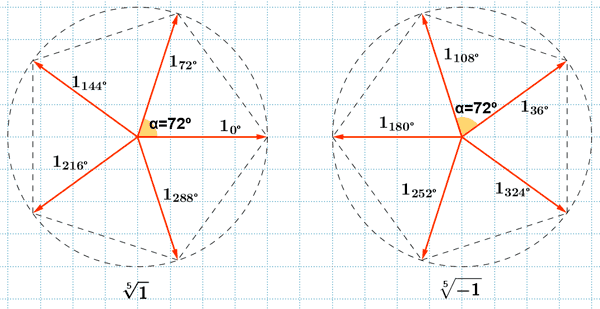
Sabemos que la tangente de un ángulo vale 0 en 0o y 180o . Como el afijo de z es (-1, 0) el ángulo del número complejo es 180o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
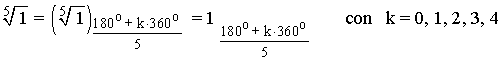
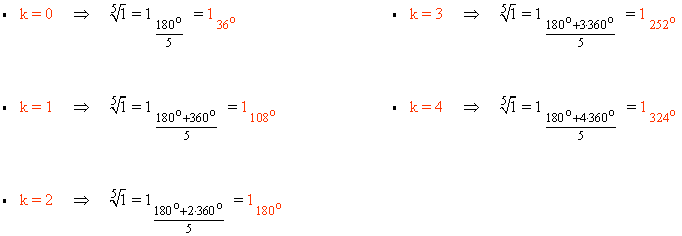
![]()
En primer lugar pasamos el número complejo a forma polar:
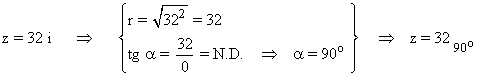
Sabemos que la tangente de un ángulo no está definida en 90o y 270o . Como el afijo de z es (0, 32) el ángulo del número complejo es 90o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
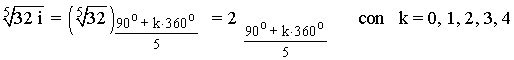
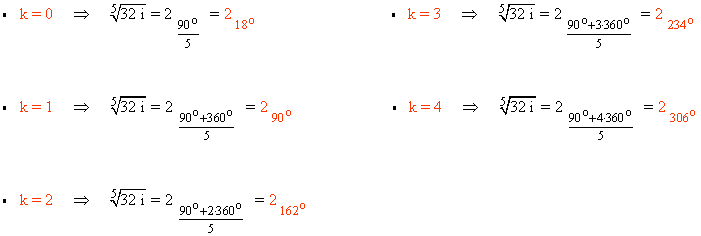
![]()
En primer lugar pasamos el número complejo a forma polar:
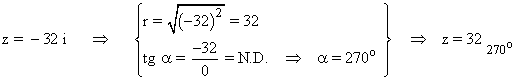
Sabemos que la tangente de un ángulo no está definida en 90o y 270o . Como el afijo de z es (0, -32) el ángulo del número complejo es 270o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
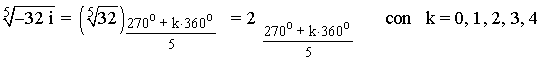
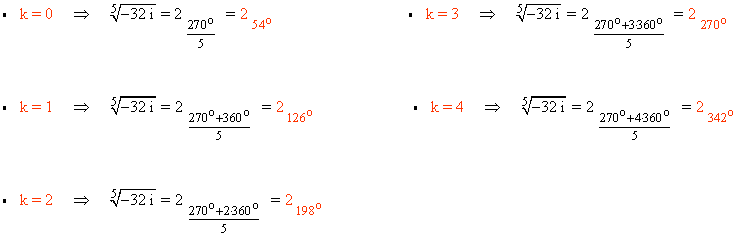
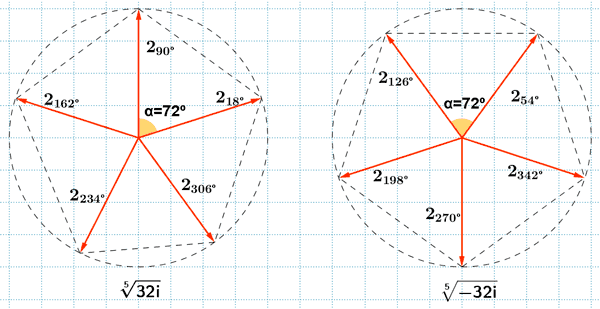
3) Calcula y expresa en forma polar:
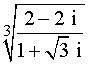
En primer lugar calculamos la forma polar del radicando:
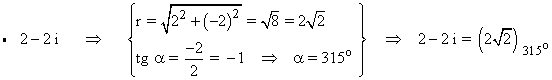
Sabemos que la tangente de un ángulo vale -1 en 135o y 315o .
Como el afijo es (2, -2) el ángulo está en el tercer cuadrante, es decir es 315o .
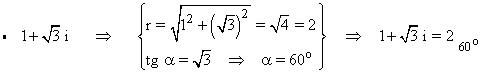
Como el afijo es (1, √3) el ángulo está en el primer cuadrante, es decir es 60o .
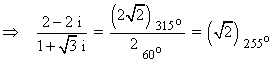
A continuación aplicamos la fórmula para encontrar las raíces cúbicas del número complejo:

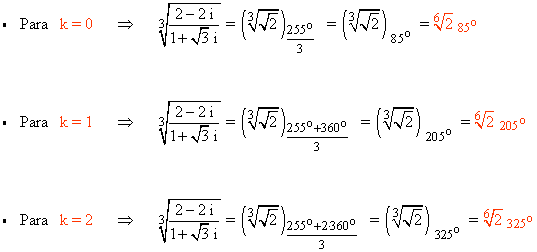
4) Calcula las raíces cúbicas del siguiente número complejo y expresa el resultado en forma polar:

![]()
En primer lugar calculamos la forma polar del radicando:
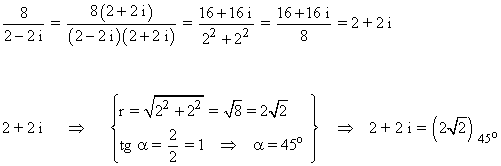
Sabemos que la tangente de un ángulo vale 1 en 45o y 225o .
Como el afijo es (2, 2) el ángulo está en el primer cuadrante, es decir es 45o .
A continuación aplicamos la fórmula para encontrar las raíces cúbicas del número complejo:
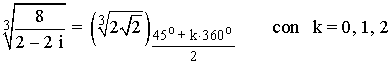
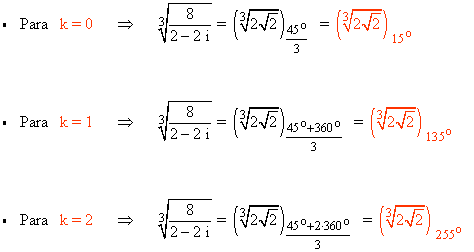
![]()
En primer lugar calculamos la forma polar del radicando:
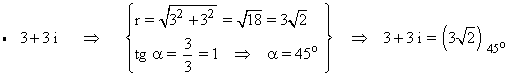
Sabemos que la tangente de un ángulo vale 1 en 45o y 315o .
Como el afijo es (3, 3) el ángulo está en el primer cuadrante, es decir es 45o .
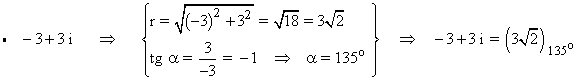
Como el afijo es (-3, 3) el ángulo está en el segundo cuadrante, es decir es 135o .

A continuación aplicamos la fórmula para encontrar las raíces cúbicas del número complejo:
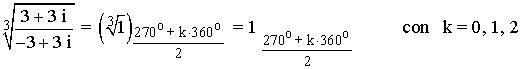
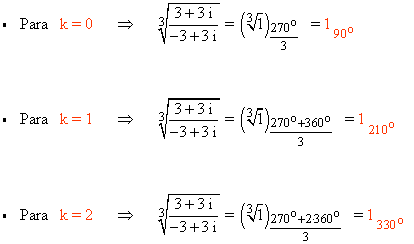
5) Halla las raíces sextas de la unidad expresando el resultado en forma polar, binómica y trigonométrica y representa gráficamente.
![]()
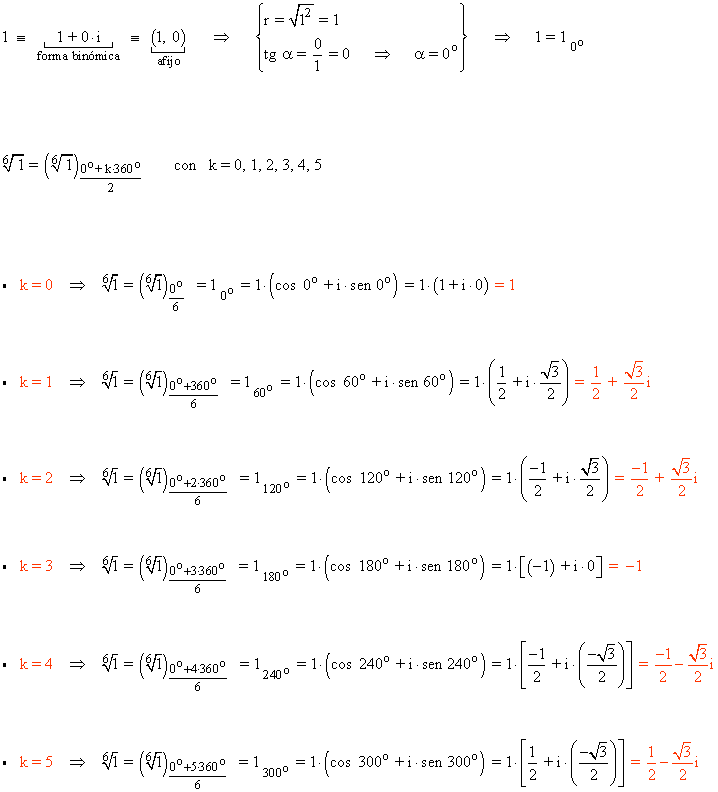
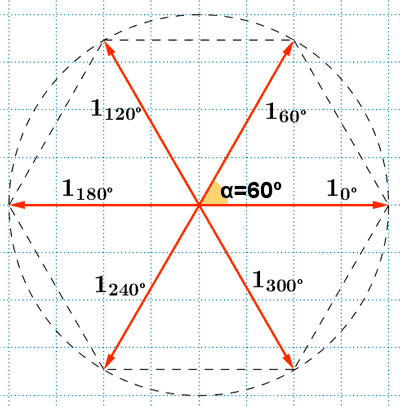
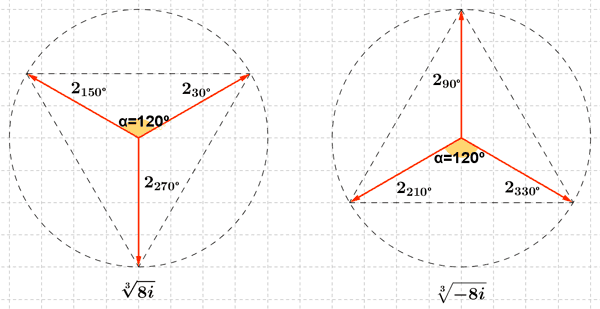
Por lo tanto, las raíces sextas de la unidad son:
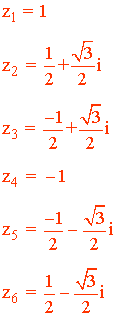
6) Halla las raíces cuartas de 81 expresando el resultado en forma polar, binómica y trigonométrica y representa gráficamente.
![]()
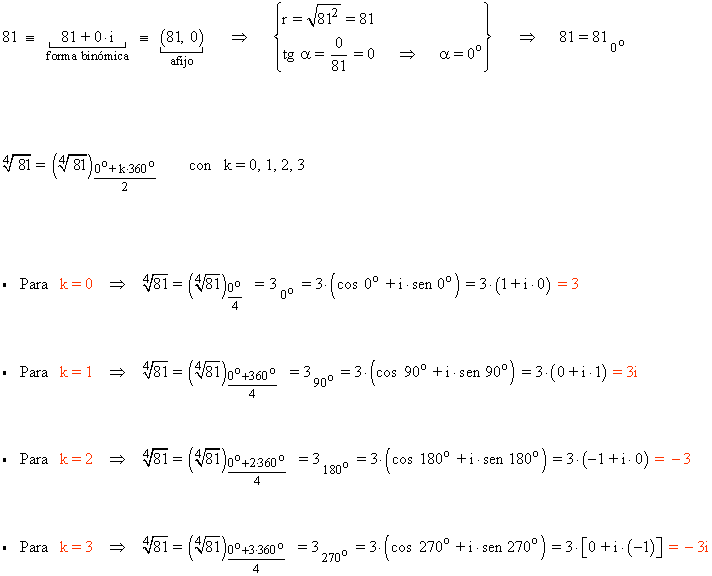
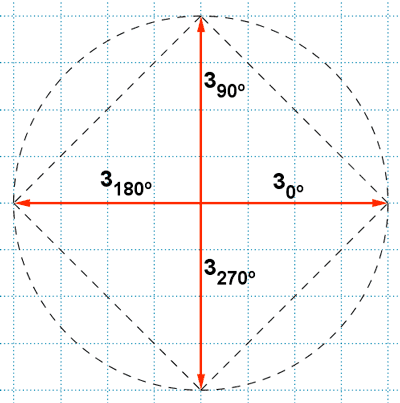
Por lo tanto, las cuatro raíces de 81 son:
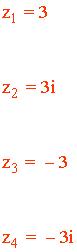
7) Calcula las siguientes raíces expresando el resultado en forma polar, binómica y trigonométrica y representa gráficamente.

![]()
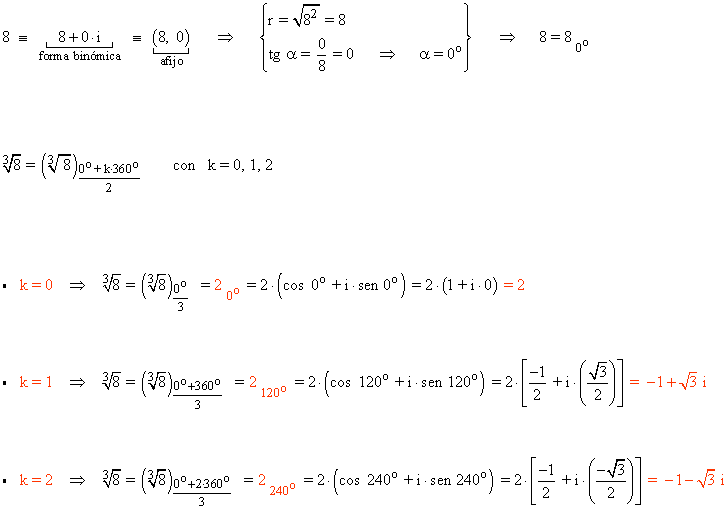
![]()
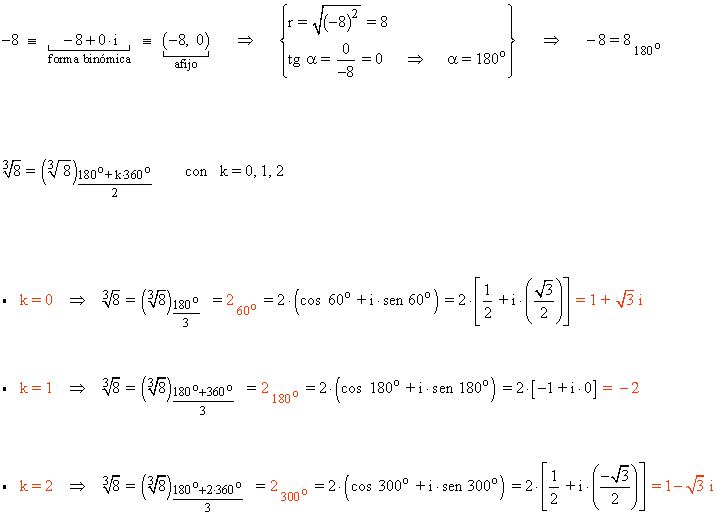
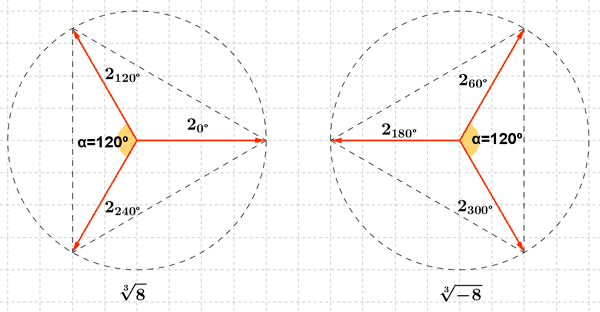
![]()
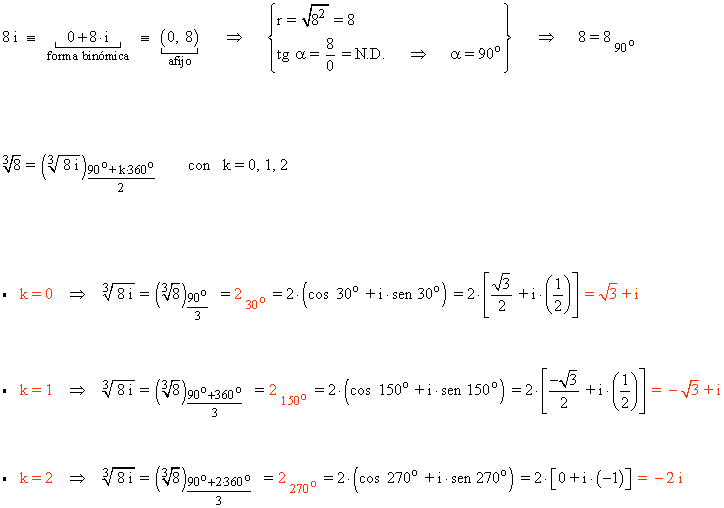
![]()
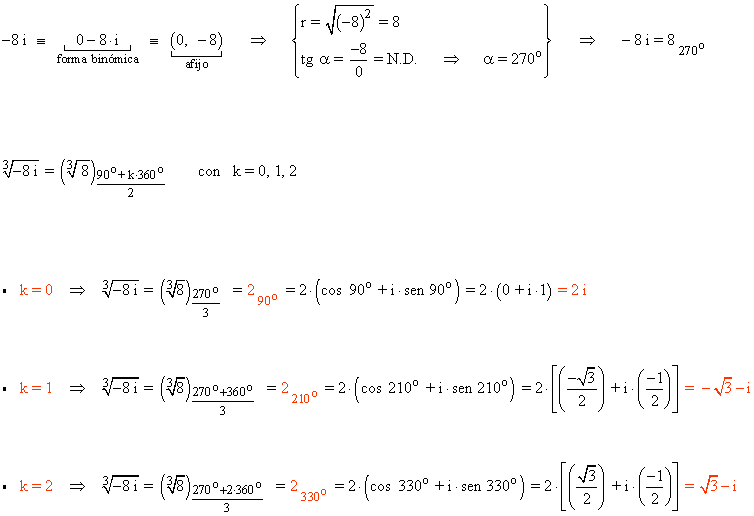
8) Calcula las siguientes raíces expresando el resultado en forma polar.

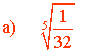
En primer lugar pasamos el número complejo a forma polar:
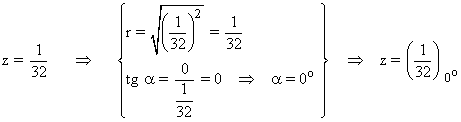
Sabemos que la tangente de un ángulo es 0 en 0o y 180o . Como el afijo de z es (1/32, 0) el ángulo del número complejo es 0o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
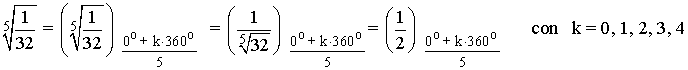
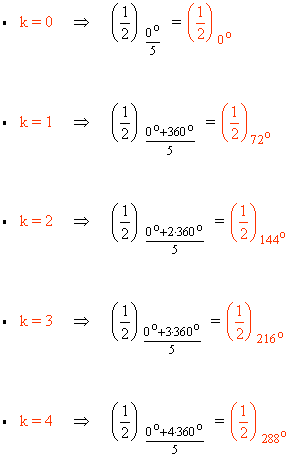
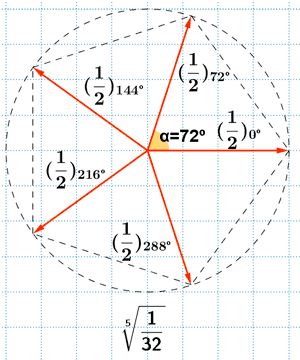
![]()
En primer lugar pasamos el número complejo a forma polar:
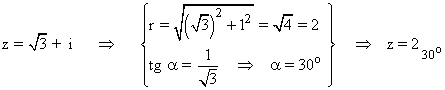
Como el afijo es (√3, 1) , es decir, está en el primer cuadrante, entonces el ángulo del número complejo es 30o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
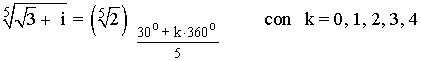
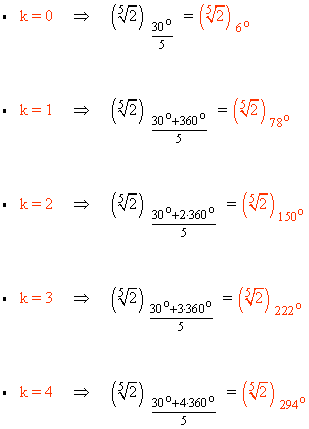
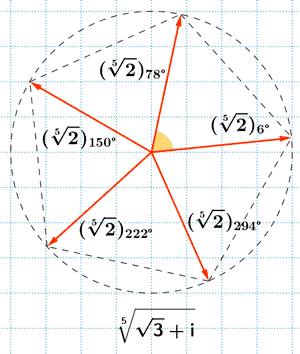
9) Calcula las siguientes raíces expresando el resultado en forma polar.
![]()
![]()
En primer lugar pasamos el número complejo a forma polar:
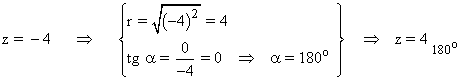
Sabemos que la tangente de un ángulo es 0 en 0o y 180o . Como el afijo de z es (-4, 0) el ángulo del número complejo es 180o . A continuación aplicamos la fórmula para encontrar las raíces cuadradas de z:
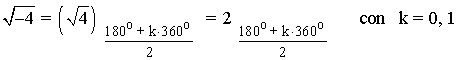
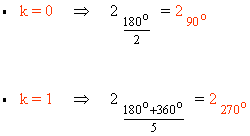
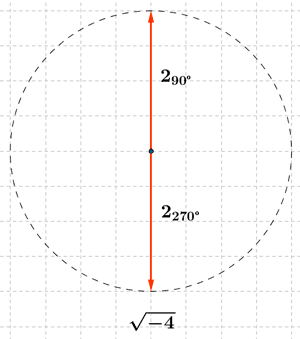
![]()
En primer lugar pasamos el número complejo a forma polar:
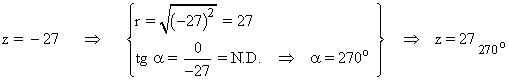
Como el afijo es (-27, 0) entonces el ángulo del número complejo es 270o . A continuación aplicamos la fórmula para encontrar las raíces quintas de z:
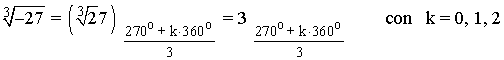
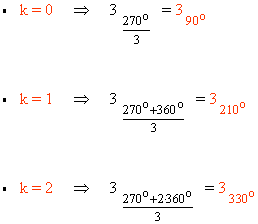
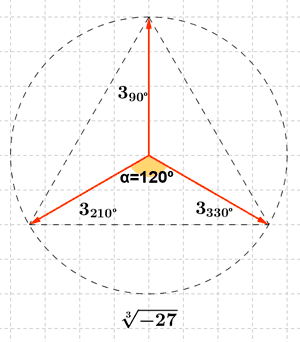
10) Calcula las siguientes raíces expresando el resultado en forma polar.

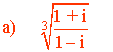
En primer lugar pasamos el número complejo a forma polar:
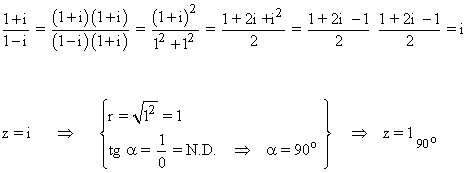
Sabemos que la tangente no está definida en 90o y 270o . Como el afijo de z es (0, 1) el ángulo del número complejo es 90o . A continuación aplicamos la fórmula para encontrar las raíces cúbicas de z:
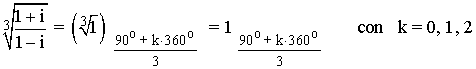
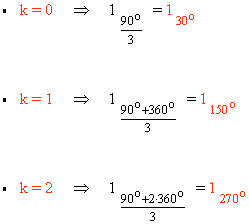
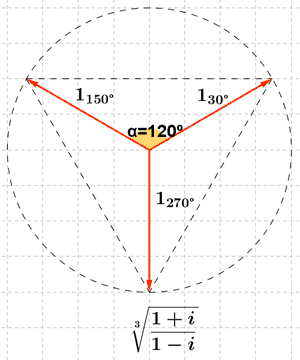
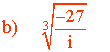
En primer lugar pasamos el número complejo a forma polar:
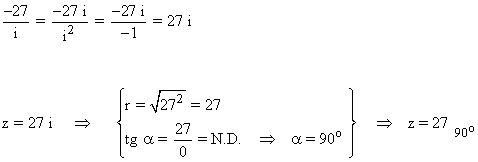
Sabemos que la tangente no está definida en 90o y 270o . Como el afijo de z es (0, 27) el ángulo del número complejo es 90o . A continuación aplicamos la fórmula para encontrar las raíces cúbicas de z:
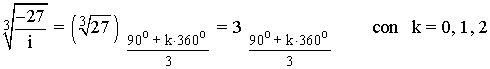
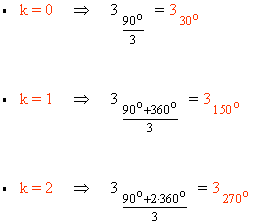
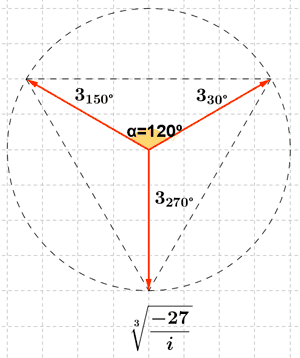
11) Calcula las siguientes raíces expresando el resultado en forma polar.
![]()
![]()
![]()
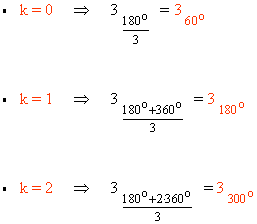
![]()



 INICIO
INICIO