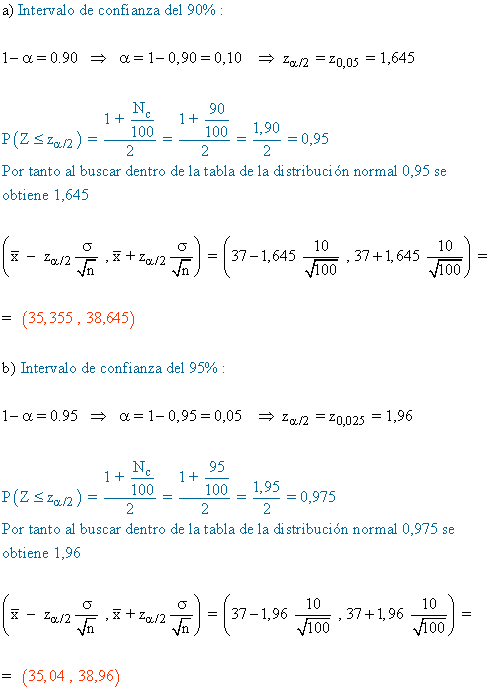Problemas resueltos de intervalos de confianza para la media poblacional.
1) Se ha tomado una muestra aleatoria de 100 individuos a los que se les ha preguntado la cantidad de dinero que tienen en la cartera, obteniéndose una media muestral de 110 €. Se sabe que la desviación típica de la población es de 20 €.
a) Obtener un intervalo de confianza, al 90%, para la cantidad de dinero en la cartera de la población.
b) ¿Cuál es el error máximo cometido con la estimación anterior?
c) Si deseamos que el error cometido, con el mismo nivel de confianza, sea la décima parte dele apartado anterior, ¿cuál ha de ser el tamaño de la muestra?2) Un estudio estadístico realizado a 49 personas nos dice que el tiempo de conexión anual a internet de los habitantes de una ciudad sigue una distribución normal de media 250 minutos y desviación típica 30 minutos. Halla el intervalo de confianza, con un nivel de confianza del 95 %, para el tiempo medio de conexión a internet.
3) La vida media de un determinado modelo de bombilla sigue una distribución normal con desviación típica igual a 60 días. Elegida una muestra y con un nivel de confianza del 98% se obtiene el intervalo (388,68 , 407,32) para la vida media. Calcule la media y el tamaño de la muestra elegida. Detalle los pasos realizados para obtener los resultados.
4) El peso de los alumnos de bachillerato de cierta ciudad tiene una media desconocida y una desviación típica σ = 5,4 kg. Tomamos una muestra aleatoria de 100 alumnos de bachillerato de esa ciudad. Si la media de la muestra es de 60 Kg, calcula con un nivel de confianza del 99% el intervalo de confianza para el peso medio de todos los alumnos de bachillerato de la ciudad.
5) Un fabricante de pilas alcalinas sabe que el tiempo de duración, en horas, de las pilas que fabrica sigue una distribución normal de media desconocida y varianza 3600.
Con una muestra de su producción elegida al azar y un nivel de confianza del 95% ha obtenido para la media el intervalo de confianza (372,6 , 392,2).
a) Calcula el valor que obtuvo para la media de la muestra y el tamaño muestral utilizado.
b) ¿Cuál sería el error de su estimación si hubiese utilizado una muestra de tamaño 225 y un nivel de confianza del 86,9 % ?6) Se sabe que una variable estadística se comporta como N(μ , 10). Para estimar μ se extrae una muestra de tamaño 100, cuya media resulta ser igual a 37. Determina el tamaño de la muestra si se desea que el error cometido al estimar μ con un nivel de confianza del 99 % no exceda de 0,2575.
7) En una población, una variable aleatoria sigue una ley normal de media desconocida y desviación típica 2. Observada una muestra de tamaño 400, tomada al azar, se ha obtenido una media muestral igual a 50. Con un nivel de confianza del 97 %, ¿qué tamaño mínimo debe tener la muestra para que la amplitud del intervalo que se obtenga sea, como máximo, 1?
8) Sabemos que una variable estadística se comporta como una N(μ , 10). Para estimar μ extraemos una muestra de tamaño 100, cuya media resulta ser igual a 37. Estima μ mediante un intervalo de confianza del 90 % y del 95 % .
9) El peso de los niños varones a las 10 semanas de vida se distribuye según una normal con desviación típica de 87 g.
¿Cuántos datos son suficientes para estimar, con una confianza del 95 %, el peso medio de esa población con un error no superior a 15 g?10) El tiempo en minutos dedicado a escuchar música por los estudiantes de secundaria de una cierta ciudad se supone que es una variable aleatoria con distribución normal de desviación típica igual a 15 minutos. Se toma una muestra aleatoria simple de 10 estudiantes y se obtienen los siguientes tiempos (en minutos):
91 68 39 82 55 70 72 62 54 67 a) Determínese un intervalo de confianza al 90 % para el tiempo medio diario dedicado a escuchar música por un estudiante.
b) Calcúlese el tamaño muestral mínimo necesario para conseguir una estimación de la media del tiempo diario dedicado a escuchar música con un error menor que 5 minutos, con un nivel de confianza del 95 %.11) Un estudio realizado sobre 144 usuarios de automóviles revela que la media anual de kilómetros recorridos es de 18 000. Si el número de km recorridos anualmente sigue una distribución normal con desviación típica de 2000 km:
a) Calcula, con una probabilidad del 97 %, entre qué valores estará la media del número de km recorridos anualmente por la población total de usuarios de automóviles.
b) Interpreta el significado del intervalo obtenido.12) Un psicólogo escolar quiere estimar la media de tiempo de reacción de los alumnos de 1º de Primaria. Para ello ha elegido una muestra de 35 niños y ha obtenido los siguientes tiempos de reacción en minutos:
1,3 ; 0,8 ; 1,1 ; 1,0 ; 1,2 ; 0,9 ; 1,5 ; 0,6 ; 1,2 ; 1,4 ; 1,3 ; 1,1 ; 1,2 ; 1,5 ; 1,3 ; 0,9 ; 1,2 ; 1,3 ; 1,1 ; 1,5 ; 0,8 ; 0,9 ; 1,1 ; 1,2 ; 1,4 ; 1,2 ; 0,9 ; 1,0 ; 1,1 ; 1,0 ; 1,2 ; 0,9 ; 0,8 ; 1,1 ; 1,1 .
Halla el intervalo de confianza para la media de tiempo de reacción al nivel del 90%.
13) Realizamos 100 lanzamientos de un dado. ¿Cuántos cuatros debemos obtener, como mínimo y como máximo, para aceptar que el dado no está trucado a un nivel de confianza del 99 % ?
14) La duración de la vida de una determinada especie de tortuga se supone que es una variable aleatoria, con distribución normal de desviación típica igual a 10 años. Se tomauna muestra aleatoria simple de 10 tortugas y se obtienen las siguientes duraciones, en años :
46, 38, 59, 29, 34, 32, 38, 21, 44, 34
Determínese un intervalo de confianza al 95 % para la vida media de dicha especie de tortuga.
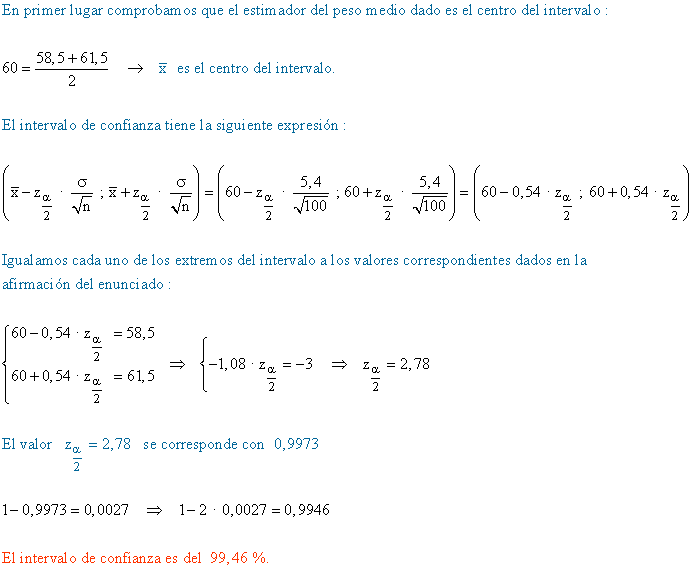
15) El peso de los usuarios de un gimnasio tiene una media desconocida y una desviación típica σ = 5,4 kg. Tomamos una muestra aleatoria de 100 usuarios obteniendo una media de 60 kg.
Se realiza la siguiente afirmación : "el peso medio de un usuario de ese gimnasio está comprendido entre 58,5 y 61,5". ¿Con qué probabilidad esta afirmación es correcta?
1) Se ha tomado una muestra aleatoria de 100 individuos a los que se les ha preguntado la cantidad de dinero que tienen en la cartera, obteniéndose una media muestral de 110 €. Se sabe que la desviación típica de la población es de 20 €.
a) Obtener un intervalo de confianza, al 90%, para la cantidad de dinero en la cartera de la población.
b) ¿Cuál es el error máximo cometido con la estimación anterior?
c) Si deseamos que el error cometido, con el mismo nivel de confianza, sea la décima parte dele apartado anterior, ¿cuál ha de ser el tamaño de la muestra?

2) Un estudio estadístico realizado a 49 personas nos dice que el tiempo de conexión anual a internet de los habitantes de una ciudad sigue una distribución normal de media 250 minutos y desviación típica 30 minutos. Halla el intervalo de confianza, con un nivel de confianza del 95 %, para el tiempo medio de conexión a internet.

3) La vida media de un determinado modelo de bombilla sigue una distribución normal con desviación típica igual a 60 días. Elegida una muestra y con un nivel de confianza del 98% se obtiene el intervalo (388,68 , 407,32) para la vida media. Calcule la media y el tamaño de la muestra elegida. Detalle los pasos realizados para obtener los resultados.
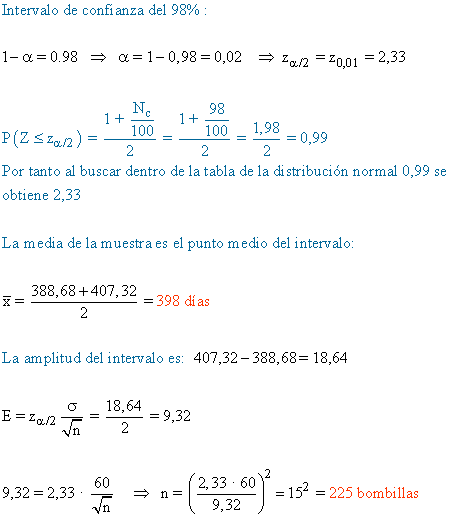
4) El peso de los alumnos de bachillerato de cierta ciudad tiene una media desconocida y una desviación típica σ = 5,4 kg. Tomamos una muestra aleatoria de 100 alumnos de bachillerato de esa ciudad. Si la media de la muestra es de 60 Kg, calcula con un nivel de confianza del 99% el intervalo de confianza para el peso medio de todos los alumnos de bachillerato de la ciudad.

5) Un fabricante de pilas alcalinas sabe que el tiempo de duración, en horas, de las pilas que fabrica sigue una distribución normal de media desconocida y varianza 3600.
Con una muestra de su producción elegida al azar y un nivel de confianza del 95% ha obtenido para la media el intervalo de confianza (372,6 , 392,2).
a) Calcula el valor que obtuvo para la media de la muestra y el tamaño muestral utilizado.
b) ¿Cuál sería el error de su estimación si hubiese utilizado una muestra de tamaño 225 y un nivel de confianza del 86,9 % ?

6) Se sabe que una variable estadística se comporta como N(μ , 10). Para estimar μ se extrae una muestra de tamaño 100, cuya media resulta ser igual a 37. Determina el tamaño de la muestra si se desea que el error cometido al estimar μ con un nivel de confianza del 99 % no exceda de 0,2575.
7) En una población, una variable aleatoria sigue una ley normal de media desconocida y desviación típica 2. Observada una muestra de tamaño 400, tomada al azar, se ha obtenido una media muestral igual a 50. Con un nivel de confianza del 97 %, ¿qué tamaño mínimo debe tener la muestra para que la amplitud del intervalo que se obtenga sea, como máximo, 1?

8) Sabemos que una variable estadística se comporta como una N(μ , 10). Para estimar μ extraemos una muestra de tamaño 100, cuya media resulta ser igual a 37. Estima μ mediante un intervalo de confianza del 90 % y del 95 % .
9) El peso de los niños varones a las 10 semanas de vida se distribuye según una normal con desviación típica de 87 g.
¿Cuántos datos son suficientes para estimar, con una confianza del 95 %, el peso medio de esa población con un error no superior a 15 g?

10) El tiempo en minutos dedicado a escuchar música por los estudiantes de secundaria de una cierta ciudad se supone que es una variable aleatoria con distribución normal de desviación típica igual a 15 minutos. Se toma una muestra aleatoria simple de 10 estudiantes y se obtienen los siguientes tiempos (en minutos):
| 91 | 68 | 39 | 82 | 55 |
| 70 | 72 | 62 | 54 | 67 |
a) Determínese un intervalo de confianza al 90 % para el tiempo medio diario dedicado a escuchar música por un estudiante.
b) Calcúlese el tamaño muestral mínimo necesario para conseguir una estimación de la media del tiempo diario dedicado a escuchar música con un error menor que 5 minutos, con un nivel de confianza del 95 %.
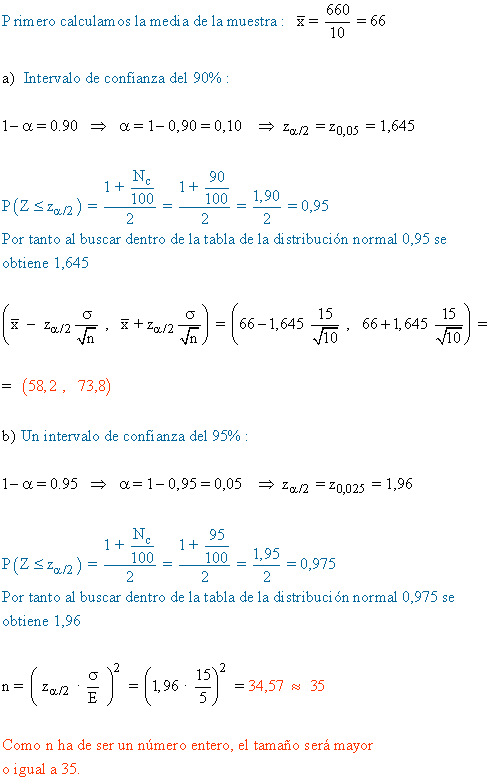
11) Un estudio realizado sobre 144 usuarios de automóviles revela que la media anual de kilómetros recorridos es de 18 000. Si el número de km recorridos anualmente sigue una distribución normal con desviación típica de 2000 km:
a) Calcula, con una probabilidad del 97 %, entre qué valores estará la media del número de km recorridos anualmente por la población total de usuarios de automóviles.
b) Interpreta el significado del intervalo obtenido.

12) Un psicólogo escolar quiere estimar la media de tiempo de reacción de los alumnos de 1º de Primaria. Para ello ha elegido una muestra de 35 niños y ha obtenido los siguientes tiempos de reacción en minutos:
1,3 ; 0,8 ; 1,1 ; 1,0 ; 1,2 ; 0,9 ; 1,5 ; 0,6 ; 1,2 ; 1,4 ; 1,3 ; 1,1 ; 1,2 ; 1,5 ; 1,3 ; 0,9 ; 1,2 ; 1,3 ; 1,1 ; 1,5 ; 0,8 ; 0,9 ; 1,1 ; 1,2 ; 1,4 ; 1,2 ; 0,9 ; 1,0 ; 1,1 ; 1,0 ; 1,2 ; 0,9 ; 0,8 ; 1,1 ; 1,1 .
Halla el intervalo de confianza para la media de tiempo de reacción al nivel del 90%.

13) Realizamos 100 lanzamientos de un dado. ¿Cuántos cuatros debemos obtener, como mínimo y como máximo, para aceptar que el dado no está trucado a un nivel de confianza del 99 % ?

14) La duración de la vida de una determinada especie de tortuga se supone que es una variable aleatoria, con distribución normal de desviación típica igual a 10 años. Se tomauna muestra aleatoria simple de 10 tortugas y se obtienen las siguientes duraciones, en años :
46, 38, 59, 29, 34, 32, 38, 21, 44, 34
Determínese un intervalo de confianza al 95 % para la vida media de dicha especie de tortuga.
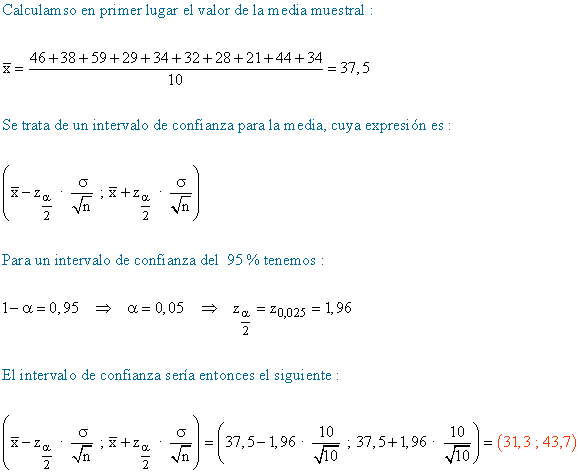
15) El peso de los usuarios de un gimnasio tiene una media desconocida y una desviación típica σ = 5,4 kg. Tomamos una muestra aleatoria de 100 usuarios obteniendo una media de 60 kg.
Se realiza la siguiente afirmación : "el peso medio de un usuario de ese gimnasio está comprendido entre 58,5 y 61,5". ¿Con qué probabilidad esta afirmación es correcta?


 INICIO
INICIO