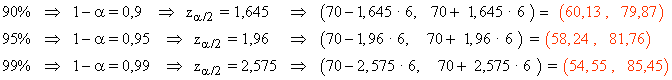Estimación por intervalos de confianza
Intervalos de confianza
- Intervalo de confianza es el intervalo que contiene al parámetro que se está estimando con un cierto nivel de confianza.
- Nivel de confianza (1 - α) , significa que el (1 - α) · 100% de los intervalos de confianza contienen el parámetro poblacional que se está estimando.
A cada nivel de confianza (Nc) le corresponde un valor crítico zα/2 correspondiente a la distribución normal N(0, 1) y que cumple:
![]()
Determinación del valor crítico zα/2
El valor crítico zα/2 correspondiente a un nivel de confianza Nc en tanto por ciento, se calcula mediante la expresión:
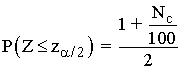
Y después buscando el resultado dentro de las tablas de la distribución normal.
Ejemplo 1:
Si fijamos el nivel de confianza Nc = 95 % hallar el valor crítico zα/2.
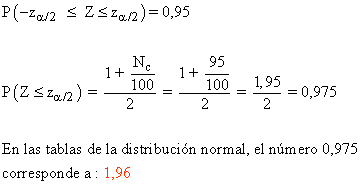
Intervalos característicos en distribuciones normales cualesquiera
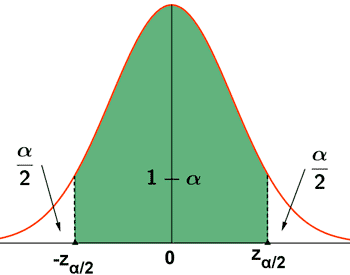
En una distribución N(μ , σ) el intervalo correspondiente a una probabilidad p = 1 -α es:
![]()
Ejemplo 2:
Hallar el intervalo característico correspondiente para:
a) 90 % b) 95 % c) 99 %
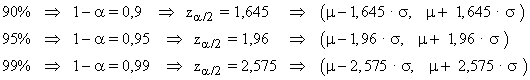
Ejemplo 3:
En una distribución normal N(70, 6) , obtener los intervalos característicos para el 90 %, 95 % y 99 %.
Ejemplo 4:
Se sabe que (45,13 , 51,03) es un intervalo de confianza, al 95%, para la media de una variable aleatoria.
a) ¿Cuál es el error cometido?
b) ¿Cuál es la media?

Ejemplo 5:
En un hospital se ha tomado la temperatura a una muestra de 82 pacientes, para estimar la temperatura media de sus pacientes. La media de la muestra ha sido de 37,6 ºC, y la desviación típica de la población, 1,08 ºC. Calcula un intervalo de confianza para la media poblacional con un nivel de confianza del 99 %.



 INICIO
INICIO