Distribución muestral de diferencia de medias.
Dos poblaciones que sigan distribuciones normales N(μ1, σ1) y N(μ2, σ2), o bien, si ambas poblaciones tienen distribuciones cualesquiera con media μ1 y μ2, desviaciones típicas σ1 y σ2, y las respectivas muestras son de tamańo n1 y n2, suficientemente grandes, entonces la distribución muestral de diferencia de medias sigue una distribución normal:
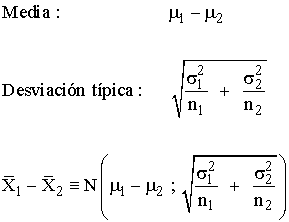
Y la variable tipificada viene dada por la expresión:
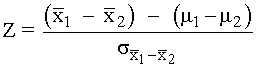
Ejemplo 1:
El responsable de la sede central de una empresa afirma que las edades de sus empleados siguen una distribución normal con una media de 41 ańos y una desviación típica de 5 ańos. Por otro lado, el responsable de una sede de las sucursales de dicha empresa en otro país, ha determinado que sus empleados también tienen edades que se ajustan a una distribución normal con una media de 39 ańos y desviación típica de 3 ańos.
Con el fin de hacer un estudio comparativo se seleccionan muestras de 40 personas de cada sede de la empresa.
a) Determina la distribución para la diferencia de las medias muestrales.
b) żCuál es la probabilidad de que los empleados de la sede central tengas una media de edad de al menos 3 ańos mayor que los de la sucursal extranjera?
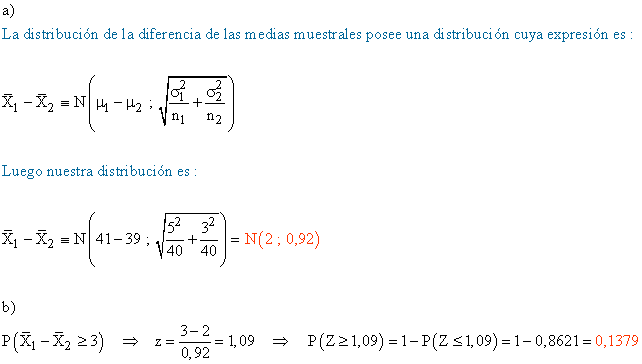
Ejemplo 2:
Las pruebas de control de calidad para un modelo A de bombilla han determinado que la duración se distribuye como una normal de media 3300 horas y desviación típica 180 horas; mientras que para otro modelo B la duración media es de 3200 horas y desviación típica 155 horas.
Si se toman muestras aleatorias de 100 bombillas de cada modelo :
a) żCuáles son los parámetros de media y desviación típica de la diferencia de las medias muestrales?
b) Halla la probabilidad de que la diferencia de las medias de las duraciones de las bombillas de cada modelo sea inferior a 40 horas.



 INICIO
INICIO

